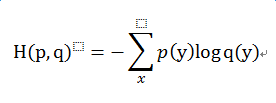熵
定义: 用来度量信息的不确定程度。
解释: 熵越大,信息量越大。不确定程度越低,熵越小,比如“明天太阳从东方升起”这句话的熵为0,因为这个句话没有带有任何信息,它描述的是一个确定无疑的事情。
例子:假设有随机变量X,用来表达明天天气的情况。X可能出现三种状态 1) 晴天2) 雨天 3)阴天 每种状态的出现概率均为P(i) = 1/3,那么根据熵的公式:
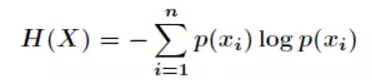
可以计算得到
H(X) = - 1/3 * log(1/3) - 1/3 * log(1/3) + 1/3 * log(1/3) = log3 =0.47712
如果这三种状态出现的概率为(0.1, 0.1, 0.8), 那么
H(X) = -0.1 * log(0.1) *2 - 0.8 * log(0.8) = 0.277528
可以发现前面一种分布X的不确定程度很高,每种状态都很有可能。后面一种分布,X的不确定程度较低,第三种状态有很大概率会出现。 所以对应前面一种分布,熵值很高,后面一种分布,熵值较低。
条件熵
定义:在一个条件下,随机变量的不确定性。
举例说明:
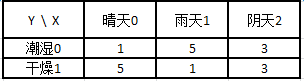
假设随机变量X表示明天的天气情况,随机变量Y表示今天的湿度,Y 有两种状态 1) 潮湿 2) 干燥。
假设基于以往的18个样本, X 的三种状态,概率均为 0.33, Y的两种状态,概率为0.5
条件概率可以通过朴素贝叶斯公式进行计算:
P(X=0|Y=0) =P(X=0,Y=0)/P(Y=0) = (1/18)/(9/18) = 1/9
P(X=1|Y=0)= P(X=1,Y=0)/P(Y=0) = (5/18)/(9/18) = 5/9
P(X=2|Y=0) =P(X=2,Y=0)/P(Y=0) = (3/18)/(9/18) = 3/9
P(X=0|Y=1) =P(X=0,Y=0)/P(Y=1) = (1/18)/(9/18) = 1/9
P(X=1|Y=1)= P(X=1,Y=0)/P(Y=1) = (5/18)/(9/18) = 5/9
P(X=2|Y=1) =P(X=2,Y=0)/P(Y=1) = (3/18)/(9/18) = 3/9
条件熵的公式:
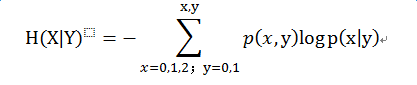
根据这个公式:
H(X|Y) = (1/18)*log(1/9) + (5/18)*log(5/9) + (3/18)*log(3/9) + (1/18)*log(1/9) + (5/18)*log(5/9) + (3/18)*log(3/9) = 0.406885
信息增益 = 熵 – 条件熵
信息增益的定义:在一个条件下,信息不确定性减少的程度
所以Y条件产生的信息增益为 0.47712 - 0.406885
信息增益的应用: 我们在利用进行分类的时候,常常选用信息增益更大的特征,信息增益大的特征对分类来说更加重要。决策树就是通过信息增益来构造的,信息增益大的特征往往被构造成底层的节点。
互信息
定义:指的是两个随机变量之间的相关程度。
理解:确定随机变量X的值后,另一个随机变量Y不确定性的削弱程度,因而互信息取值最小为0,意味着给定一个随机变量对确定一另一个随机变量没有关系,最大取值为随机变量的熵,意味着给定一个随机变量,能完全消除另一个随机变量的不确定性。这个概念和条件熵相对。
公式:
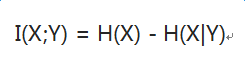
假设X,Y完全无关,H(X) = H(X|Y) , 那么I(X;Y) = 0
假设X,Y完全相关,H(X|Y) =0, 那么I(X;Y) = H(X)
条件熵越大,互信息越小,条件熵越小,互信息越大。
互信息和信息增益实际是同一个值。
交叉熵
定义:信息论中的重要概念,主要用于度量两个概率分布间的差异性信息。
理解: 在进行优化的过程中,往往将交叉熵又命名为loss变量,优化的目标即是最小化loss。
假如X为一组已知的输入特征值,Y为一组已知的输出分类。优化的目标是为了找到一个映射模型F, 使得预测值Y_ = F(X), 与真值Y最相似。但现实世界的Y和Y_的分布肯定不是完全一致的。
所以:
Y 服从 p分布(即真实分布)
Y_ 服从 q分布
交叉熵cross_entropy 即为描述p,q两个分布差异性的指标。
交叉熵公式: