前置技能
匈牙利算法
增广路
从一个未匹配点到另一个未匹配点,中间经过的匹配边和未匹配边交替出现的一条路径
从上面的性质来看
每次找到一条增广路,增广路一定有奇数条边,而且未匹配边一定比匹配边多一
那么把匹配和未匹配做一遍类似异或的操作就能使答案(+1)
如果找不到增广路那么就是最大匹配了
然后这就是匈牙利算法的思想
但是这只是对于二分图来讲的
而对于不能变成二分图的图,就不行了
比如这个
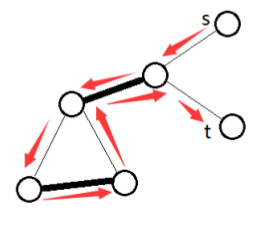
深色的为匹配边
这显然是增广路,但是显然不能这样,如果取反,肯定是不合法的
因为一个奇数的环中一点连了两条同为匹配或未匹配的边
此时就需要进行修改
带花树算法
对于每个奇环,肯定是有一个点不会和环内的点匹配的
那么我们可以不管这个环内的匹配,直接缩成一个点
只需要知道环内的走向,满足找到增广路后取反合法就好了,取反时展开环
算法过程
把点分成两类:(S)类和(T)类
每次选一个(S)点出发增广
(pre)记录每个(T)点扩展而来的(S)点
从(S)点扩展节点, 如果是走过的(T)点, 直接跳过
如果(T)没走过, 并且没有被匹配, 那么找到了一条增广路,
此时直接往回走, 找到每个(T)点的(pre), 直接匹配这两个点,
然后跳到原来(pre)匹配的点上继续往回处理
相当于是对匹配边与未匹配边进行异或操作
否则如果(T)被匹配了, 那么把它匹配的点加入队列, 继续增广
以上是匈牙利算法的过程
重点是如果遇到了走过的(S)点
此时就要进行"开花"的操作
首先找到这两个点的(LCA), 准确来讲应该是这两个点所属"花"的(LCA), 然后缩成一朵"大花", 把它看成(S)点就好了
求(LCA)就暴力求一下就好了
此时我们要考虑这朵"大花"内(pre)的变化
对于这两个点, 设为(x), (y), 它们都是(S)点, 从(x)走到了(y)
往回跳到(LCA)
每次跳到它的匹配点, 如果它是(T)点, 变成(S)点, 丢进队列内
每次它和它的匹配点直接(pre)相互连
最后(x), (y)的(pre)也相互连, 表示在同一个"花"内
每次找到增广路往回走到(x), (x)到(y)这条边是未匹配的, 此时(x)一定匹配了外面的一个点
那么就只要沿着(x)之前匹配的点往回继续走就好了
也就是说(pre)在"花"内这样连接, 就使得每次回到"花"时, 走的是那条未匹配的边回去
# include <bits/stdc++.h>
# define RG register
# define IL inline
# define Fill(a, b) memset(a, b, sizeof(a))
using namespace std;
typedef long long ll;
const int _(505);
typedef int Arr[_];
IL int Input(){
RG int x = 0, z = 1; RG char c = getchar();
for(; c < '0' || c > '9'; c = getchar()) z = c == '-' ? -1 : 1;
for(; c >= '0' && c <= '9'; c = getchar()) x = (x << 1) + (x << 3) + (c ^ 48);
return x * z;
}
Arr first, match, fa, vis, tim, pre;
int n, m, cnt, idx, ans;
queue <int> Q;
struct Edge{
int to, next;
} edge[_ * _];
IL void Add(RG int u, RG int v){
edge[cnt] = (Edge){v, first[u]}, first[u] = cnt++;
}
IL int Find(RG int x){
return x == fa[x] ? x : fa[x] = Find(fa[x]);
}
IL int LCA(RG int x, RG int y){
++idx, x = Find(x), y = Find(y);
while(tim[x] != idx){
tim[x] = idx;
x = Find(pre[match[x]]);
if(y) swap(x, y);
}
return x;
}
IL void Blossom(RG int x, RG int y, RG int p){
while(Find(x) != p){
pre[x] = y, y = match[x];
if(vis[y] == 2) vis[y] = 1, Q.push(y);
if(Find(x) == x) fa[x] = p;
if(Find(y) == y) fa[y] = p;
x = pre[y];
}
}
IL int Aug(RG int S){
while(!Q.empty()) Q.pop();
Fill(vis, 0), Fill(pre, 0);
for(RG int i = 1; i <= n; ++i) fa[i] = i;
Q.push(S), vis[S] = 1;
while(!Q.empty()){
RG int u = Q.front(); Q.pop();
for(RG int e = first[u]; e != -1; e = edge[e].next){
RG int v = edge[e].to;
if(Find(u) == Find(v) || vis[v] == 2) continue;
if(!vis[v]){
vis[v] = 2, pre[v] = u;
if(!match[v]){
for(RG int x = v, lst; x; x = lst)
lst = match[pre[x]], match[x] = pre[x], match[pre[x]] = x;
return 1;
}
vis[match[v]] = 1, Q.push(match[v]);
}
else if(vis[v] == 1){
RG int p = LCA(u, v);
Blossom(u, v, p);
Blossom(v, u, p);
}
}
}
return 0;
}
int main(RG int argc, RG char *argv[]){
Fill(first, -1);
n = Input(), m = Input();
for(RG int i = 1, u, v; i <= m; ++i)
u = Input(), v = Input(), Add(u, v), Add(v, u);
for(RG int i = 1; i <= n; ++i) if(!match[i]) ans += Aug(i);
printf("%d
", ans);
for(RG int i = 1; i <= n; ++i) printf("%d ", match[i]);
return puts(""), 0;
}