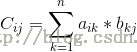矩阵,一个神奇又令人崩溃的东西,常常用来优化序列递推
在百度百科中,矩阵的定义:
在数学中,矩阵(Matrix)是一个按照长方阵列排列的复数或实数集合 ,最早来自于方程组的系数及常数所构成的方阵。这一概念由19世纪英国数学家凯利首先提出。
好,很高深对吧。那我们就更加直接地理解一下矩阵的实质:二维数组
好了这个SB都会,就不解释了
同二维数组一样,矩阵是一个'纵横排列的二维数据表格',它一般是一个n*m的二维数组,其中n*m表示它有n行m列
每一位上的数可以用下标i,j来表示,形如这样一个矩阵:

这里我们就可以用B[1][2]来表示8这个元素
矩阵有加/减/乘法(有没有除法我不知道),其中加减法的限制比较大,当且仅当两个矩阵的行列数都相等时才能进行加减
加减的操作也很简单,只需要按位加减即可
这些都是次要的,最主要的其实是矩阵乘法
我们定义矩阵乘法:设A为m*p的矩阵,B为p*n的矩阵,那么称m*n的矩阵C为矩阵A与B的乘积,记作C=AB,其中矩阵C中的第i行第j列元素可以表示为:
这样我们就很轻松的得到了一个O(n^3)的矩阵乘法,虽然还有更快的,但一般来说已经足够
矩阵乘法有以下几条重要性质:
-
矩阵乘法满足集合律,即(AB)C=A(BC)
-
矩阵乘法满足分配律,即(A+B)C=AC+BC
-
矩阵乘法一般不满足交换律
以上第三条就告诉我们,平时写两个数相乘的时候可以为所欲为,但是矩阵就完全不同了,AB!=BA
很简单,结合矩阵乘法来理解下。
换句更简单的,甚至交换后这两个矩阵都无法相乘,因为他们的列数可能就不相等了
然后我们又由于第一条可以得出矩阵快速幂的算法
首先矩阵幂只有方阵(即行数等于列数的矩阵)才可以做,要不然到后面都乘不了了(还是因为列数不相等了)
这个也很简单,我们只需要把一般的快速幂乘法部分改成矩阵乘法即可
还是一句话:不要乘反了!
对了,还要引出一个叫单位矩阵的东西,这个就好比一般乘法中的单位1一样。任何一个矩阵乘上单位矩阵都得到原来这个矩阵
单位矩阵为:

就是一个矩阵对角线上都是1
自己动手推一下就可以更深刻地理解一下了
然后我们就引出我们讨论的问题:斐波那契数列的矩阵优化
例题:Luogu P1962 斐波那契数列,求斐波那契数列的第n项%一个数的值
我们可以利用矩阵在线性代数和方程的作用在解决这个问题
我们考虑一个矩阵:
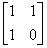
然后我们用一个列向量(就是列数为1的矩阵)来表示一下当前状态下斐波那契数列的值,由于斐波那契数列只要用到前两项,因此我们可以设:

然后我们让这两个矩阵相乘,得到新的矩阵:
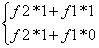
上面的这一项不就是斐波那契的递推式了吗?而且下面的这一项刚好可以为下一次做准备
因此我们只需要把原来的[1,1]列向量乘斐波那契的递推矩阵(n-2)次即可(注意前面的两项就是初始值)
但是如果就是这样的话就太慢了,因此我们又联想到矩阵乘法的结合律
即直接先求出斐波那契矩阵的(n-2)次,然后再与[1,1]的列向量相乘即可
再简化后就是斐波那契矩阵的(n-2)次的[1][1]与[1][2]上值的和
这样就完成了矩阵的第一步也是最简单,最基础的一步
注意矩阵一般的写法还是写成结构体比较好
由于这里的矩阵大小都是确定的,就没有在矩阵中记录行列数了,一般情况下都是以记录为主
好了接下来给出CODE
#include<cstdio>
using namespace std;
typedef long long LL;
const LL N=3,mod=1000000007;
LL F[N],ans[N];
struct Matrix
{
LL a[N][N];
inline void init(void)
{
a[1][1]=a[2][2]=1;
a[1][2]=a[2][1]=0;
}
inline void Fb_init(void)
{
a[1][1]=a[1][2]=a[2][1]=1;
a[2][2]=0;
}
};
inline Matrix mul(Matrix A,Matrix B)
{
register int i,j,k;
Matrix C;
for (i=1;i<N;++i)
for (j=1;j<N;++j)
for (C.a[i][j]=0,k=1;k<N;++k)
C.a[i][j]=(C.a[i][j]+A.a[i][k]*B.a[k][j])%mod;
return C;
}
inline Matrix quick_pow(Matrix A,LL p)
{
Matrix B; B.init();
while (p)
{
if (p%2) B=mul(B,A);
A=mul(A,A); p/=2;
}
return B;
}
int main()
{
register int i,j;
LL n; scanf("%lld",&n);
if (n<=2) { puts("1"); return 0; }
n-=2; F[1]=F[2]=1;
Matrix A; A.Fb_init();
A=quick_pow(A,n);
printf("%lld",(A.a[1][1]+A.a[1][2])%mod);
return 0;
}
(以上的一部分图片来自百度百科,一部分来自于Luogu憧憬未来 dalao)的题解