矩阵二分乘

题目描述：: 给定a0,a1,以及an=p*a(n-1) + q*a(n-2)中的p,q。这里n >= 2。求第k个数对10000的模。

输入：: 输入包括5个整数：a0、a1、p、q、k。

输出：: 第k个数a(k)对10000的模。

样例输入：

20 1 1 14 5

样例输出：

来源：: 2009年清华大学计算机研究生机试真题


看到这个题目，如果按照最普通的方法（根据递推公式，带入每组输入的数，最后对a(k)求余），这样多半会超时。因为结果要对10000取模，所以我想到找规律，测试了几组数据发现很难找到什么规律。哎~~输入的变量太多了，不好控制。
没办法，上网看到有人说用矩阵二分乘来做。What？矩阵二分乘是什么东东？弱爆了~~~下面引用了jzlikewei的文章里的内容，从快速取幂到矩阵二分乘。

快速取幂：

利用分治思想进行:

A^p=(A^(p/2))*(A^(p/2)) //p为偶数

A^p=(A^(p/2))*(A^(p/2)) *A //p为奇数

那么如何求A^(p/2),依旧用上面的两个式子，直至p=1。

一个递归程序就得到了：

longlong Qexp (int A, int p )

{

if (p==1)

return(A );

// if(0==p)

//　　　　return 1;

longlong tmp=Qexp(A,p/2);

if ( p %2 ==0)

return(tmp *tmp );

return(tmp*tmp*A);

}

矩阵二分乘

很多递推关系通常并不是一个前项对应一个后项的，二对一甚至多对一都是可能，一个臭名昭著著名的例子就是斐波那契数列(F[i]=f[i-1]+f[i-2],f[0]=0;f[1]=1)，这些式子很难写出通项公式。

以斐波那契数列数列举例,如何快速求出第N项？

考虑矩阵乘法:

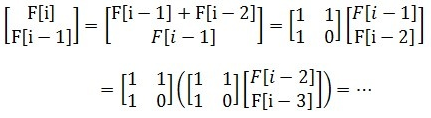
矩阵乘法满足结合律。

那么，得到:

这样问题就变成了求出系数矩阵的i-1次幂了。显然，可以通过快随取幂来做，只需要将快速取幂中的乘法换成矩阵乘法即可。

（不要问我，这个是怎么想到的，线性代数这门课从没有告诉我，矩阵、行列式有什么用，怎么用。）

一般的，对于f[n]=a1f[n-1]+a2f[n-2]+…+aif[n-i]

有：

这个很容易推导出来的。

那么，渐进时间复杂度由原来的O(n)变成了O(Tlogn)，其中T为矩阵乘法的时间复杂度，与矩阵大小有关，logn表示以2为底的n的对数，忽略常数项为O(logn).

千万不要小看这O(logn)和O(n)的区别，如果你很大，比如n=2^20=1048576，那logn=20。

而这一题，根据递推公式变换成矩阵形式

| a(n) | = | p q | n-1 * | a(1) |

| a(n-1) | | 1 0 | | a(0) |

下面就是隆重的贴代码的环节，今天大年三十，祝大家新年快乐啦！！！

#include <iostream>
#include <cstdio>
using namespace std;
struct Matrix_2_2
{
    int a[2][2];
    Matrix_2_2 operator*(Matrix_2_2 &m)
    {
        Matrix_2_2 new_m;
        new_m.a[0][0]=(a[0][0]*m.a[0][0]+a[0][1]*m.a[1][0])%10000;
        new_m.a[0][1]=(a[0][0]*m.a[0][1]+a[0][1]*m.a[1][1])%10000;
        new_m.a[1][0]=(a[1][0]*m.a[0][0]+a[1][1]*m.a[1][0])%10000;
        new_m.a[1][1]=(a[1][0]*m.a[0][1]+a[1][1]*m.a[1][1])%10000;
        return new_m;
    }
};
 
Matrix_2_2 MatrixPower(Matrix_2_2 &m,int n)
{
    if(0==n)
    {
        Matrix_2_2 m0;
        m0.a[0][0]=1;
        m0.a[0][1]=0;
        m0.a[1][0]=0;
        m0.a[1][1]=1;
        return m0;
    }
    Matrix_2_2 temp;
    temp=MatrixPower(m,n/2);
    if(n&1)
        return temp*temp*m;
    else
        return temp*temp;
}
int main()
{
    int a0,a1,p,q,k;
    Matrix_2_2 m,m_last;
    while(scanf("%d%d%d%d%d",&a0,&a1,&p,&q,&k)!=EOF)
    {
        if(0==k)
        {
            printf("%d
",a0);
            continue;
        }
        if(1==k)
        {
            printf("%d
",a1);
            continue;
        }
        m.a[0][0]=p;
        m.a[0][1]=q;
        m.a[1][0]=1;
        m.a[1][1]=0;
        m_last=MatrixPower(m,k-1);
        int res=((m_last.a[0][0]*a1)%10000+(m_last.a[0][1]*a0)%10000)%10000;
        printf("%d
",res);
    }
    return 0;
}

View Code

2013,Goodbye.