声明:本文相关所有内容完全来自于退乎-回答-怎样更好地理解并记忆泰勒展开式?
原文中前一小部分不再描述,直接从文章的核心思想处说起;
本段的核心思想是仿造。
当我们想要仿造一个东西的时候,无形之中都会按照上文提到的思路,即先保证大体上相似,再保证局部相似,再保证细节相似,再保证更细微的地方相似……不断地细化下去,无穷次细化以后,仿造的东西将无限接近真品。真假难辨。
这是每个人都明白的生活经验。
一位物理学家,把这则生活经验应用到他自己的研究中,则会出现下列场景:
一辆随意行驶的小车,走出了一个很诡异的轨迹曲线:
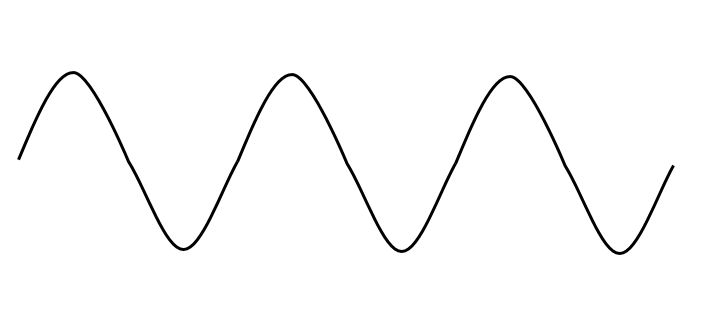
物理学家觉得这段轨迹很有意思,也想开车走一段一摸一样的轨迹。
既然是复制,他把刚才关于“仿造”生活经验应用到这里,提出了一个解决办法:
既然想模仿刚才那辆车,
那首先应该保证初始位置一样,
继续模仿,让车在初始位置的速度也一样,
不满足,继续细化,这次保持位置、在初始位置处的速度一样的同时,保证在初始位置处车的加速度也一样,
不满足,继续细化,这次保证初始位置、初始位置处的速度、初始位置处的加速度都一样,也保证初始位置处的加速度的变化率也一样,
不满足,精益求精,可以一直模仿下去。
物理学家得出结论:把生活中关于“仿造”的经验运用到运动学问题中,如果想仿造一段曲线,那么首先应该保证曲线的起始点一样,其次保证起始点处位移随时间的变化率一样(速度相同),再次应该保证前两者相等的同时关于时间的二阶变化率一样(加速度相同)……如果随时间每一阶变化率(每一阶导数)都一样,那这俩曲线肯定是完全等价的。
一位数学家,泰勒,某天看到一个函数(y=e^x) ,不由地眉头一皱,心里面不断地犯嘀咕:有些函数啊,他就是很恶心,比如这种,还有三角函数,这样的函数本来具有很优秀的品质(可以无限次求导,而且求导还很容易),但是呢,如果是代入数值计算的话,就很难了。比如,看到(y=cos x)后,我无法很方便地计算(x=2)时候的值。
为了避免这种如鲠在喉的感觉,必须得想一个办法让自己避免接触这类函数,即把这类函数替换掉。
可以根据这类函数的图像,仿造一个图像,与原来的图像相类似,这种行为在数学上叫近似。不扯这个名词。讲讲如何仿造图像。
他联想到生活中的仿造经验,联想到物理学家考虑运动学问题时的经验,泰勒首先定性地、大概地思考了一下整体思路。(下面这段只需要理解这个大概意思就可以,不用深究。)
面对(f(x)=cos x)的图像,泰勒的目的是:仿造一段一模一样的曲线(g(x)),从而避免余弦计算。
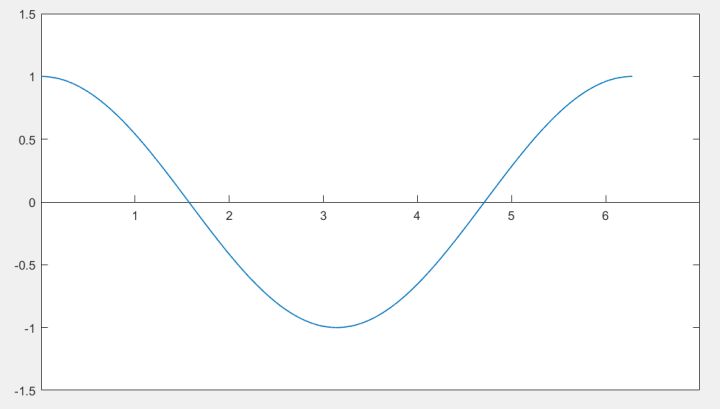
想要复制这段曲线,首先得找一个切入点,可以是这条曲线最左端的点,也可以是最右端的点,anyway,可以是这条线上任何一点。他选了最左边的点。
由于这段曲线过((0,1))这个点,仿造的第一步,就是让仿造的曲线也过这个点,
完成了仿造的第一步,很粗糙,甚至完全看不出来这俩有什么相似的地方,那就继续细节化。开始考虑曲线的变化趋势,即导数,保证在此处的导数相等。
经历了第二步,现在起始点相同了,整体变化趋势相近了,可能看起来有那么点意思了。想进一步精确化,应该考虑凹凸性。高中学过:表征图像的凹凸性的参数为“导数的导数”。所以,下一步就让二者的导数的导数相等。
起始点相同,增减性相同,凹凸性相同后,仿造的函数更像了。如果再继续细化下去,应该会无限接近。所以泰勒认为“仿造一段曲线,要先保证起点相同,再保证在此处导数相同,继续保证在此处的导数的导数相同……”
有了整体思路,泰勒准备动手算一算。
下面就是严谨的计算了。
先插一句,泰勒知道想仿造一段曲线,应该首先在原来曲线上随便选一个点开始,但是为了方便计算,泰勒选择从((0,1))这个点入手。
把刚才的思路翻译成数学语言,就变成了:
首先得让其初始值相等,即:(g(0)=f(0))
其次,得让这俩函数在x=0处的导数相等,即:(g^{'}(0)=f^{'}(0))
再次,得让这俩函数在x=0处的导数的导数相等,即:(g^{''}(0)=f^{''}(0))
……
最终,得让这俩图像在x=0的导数的导数的导数的……的导数也相同。
这时候,泰勒思考了两个问题:
第一个问题,余弦函数能够无限次求导,为了让这两条曲线无限相似,我仿造出来的(g(x))必须也能够无限次求导,那(g(x))得是什么样类型的函数呢?
第二个问题,实际操作过程中,肯定不能无限次求导,只需要求几次,就可以达到我想要的精度。那么,实际过程中应该求几次比较合适呢?
综合考虑这两个问题以后,泰勒给出了一个比较折中的方法:令(g(x))为多项式,多项式能求几次导数呢?视情况而定,比如五次多项式 (g(x)=ax^{5}+bx^{4}+cx^{3}+dx^{2}+ex+f)(chenzhen0530注:这一点是不是有问题?) ,能求5次导,继续求就都是0了,几次多项式就能求几次导数。
泰勒比我们厉害的地方仅仅在于他想到了把这种生活经验、翻译成数学语言、并运用到仿造函数图像之中。假如告诉你这种思路,静下心来你都能自己推出来。
泰勒开始计算,一开始也不清楚到底要求几阶导数。为了发现规律,肯定是从最低次开始。
先算个一阶的。
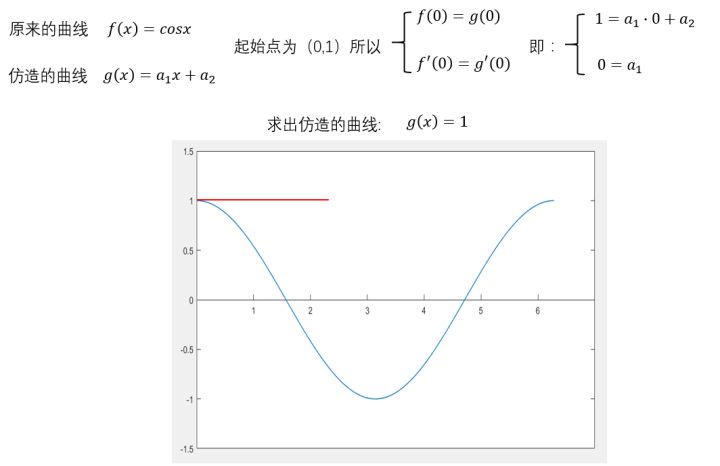
可以看出,除了在((0,1))这个点,其他的都不重合,不满意。
再来个二阶的。
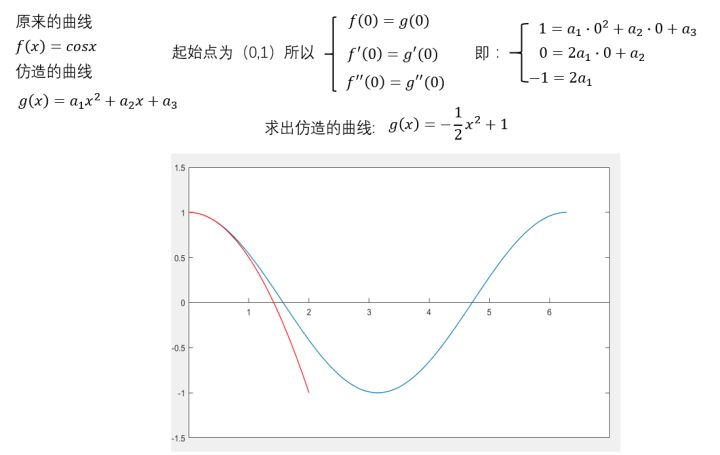
可以看出,在((0,1))这个点附近的一个小范围内,二者都比较相近。
再来个四阶的。
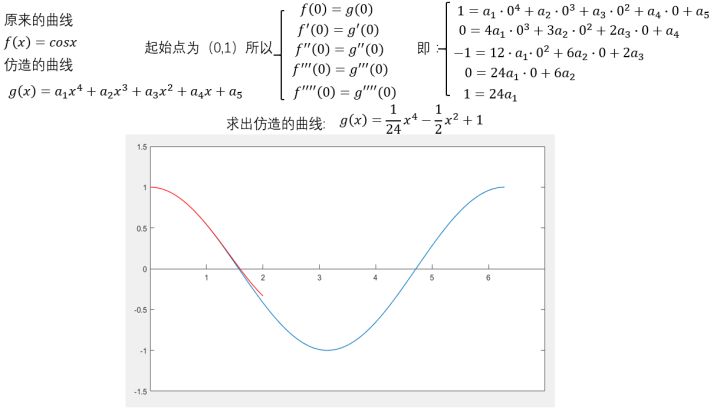
可以看出,仍然是在((0,1))这个点附近的一个范围内二者很相近。只是,此时二者重合的部分扩大了。
到这里,不光是泰勒,我们普通人也能大概想象得到,如果继续继续提高阶数,相似范围继续扩大,无穷高阶后,整个曲线都无限相似。插个图,利用计算机可以快速实现。
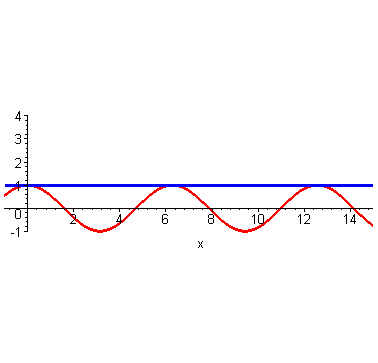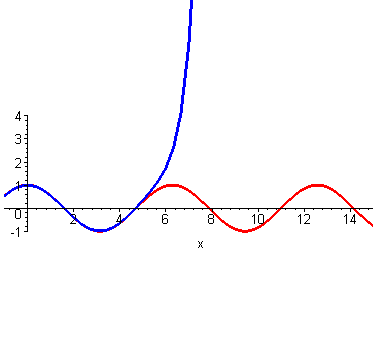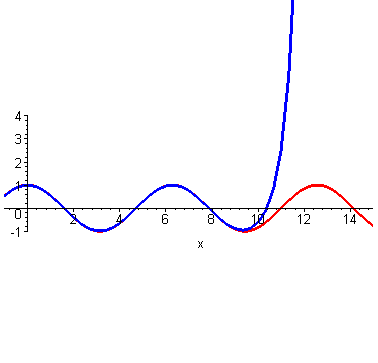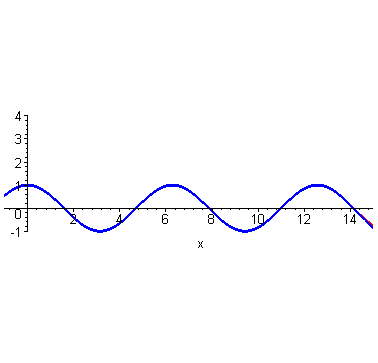
然而泰勒当时没有计算机,他只能手算,他跟我们一样,算到四阶就算不动了,他就开始发呆:刚才为什么这么做来着?哦,对了,是为了计算(cos2)的时候避免出现余弦。所以他从最左端((0,1))处开始计算,算着算着,他没耐心了,可是离着计算(x=2)还有一段距离,必须得继续算才能把这俩曲线重合的范围辐射到(x=2)处。
此时,他一拍脑门,恍然大悟,既然我选的点离着我想要的点还远,我为啥不直接选个近点的点呢,反正能从这条曲线上任何一个点作为切入,开始仿造。近了能省很多计算量啊。想计算(cos2),可以从(cosfrac{pi}{2})处开始仿造啊。
所以啊,泰勒展开式就是把一个三角函数或者指数函数或者其他比较难缠的函数用多项式替换掉。
也就是说,有一个原函数 (f(x)),我再造一个图像与原函数图像相似的多项式函数(g(x)),为了保证相似,我只需要保证这俩函数在某一点的初始值相等,1阶导数相等,2阶导数相等,……n阶导数相等。
写到这里,你已经理解了泰勒展开式。
如果能理解,即使你记不住泰勒展开式,你都能自己推导。所以,我建议你,考试之前临时死记硬背一下,即使考试因为紧张忘了,也可以现场推。如果不是为了考试,那记不住也没关系,反正记住了一段时间不用,也会忘。用的时候翻书,找不到书就自己推导。
继续说泰勒。
泰勒算到四阶以后就不想算了,所以他想把这种计算过程推广到n阶,算出一个代数式,这样直接代数就可以了。泰勒就开始了下面的推导过程。
首先要在曲线(f(x))上任选一个点,为了方便,就选((0,f(0))),设仿造的曲线的解析式为(g(x)),前面说了,仿造的曲线是一个多项式,假设算到n阶。
能求n次导数的多项式,其最高次数肯定也为n。所以,仿造的曲线的解析式肯定是这种形式:
前面说过,必须保证初始点相同,即
(g(0)=f(0)=a_0)求出了(a_0)
接下来,必须保证n阶导数依然相等,即
(g^{n}(0)=f^{n}(0))
因为对(g(x))求n阶导数时,只有最后一项为非零值,为(n!a_{n}),
由此求出(a_{n}=frac{f^{n}(0)}{n!})
求出了(a_n),剩下的只需要按照这个规律换数字即可。
综上:
知道了原理,然后把原理用数学语言描述,只需要两步即可求出以上结果。背不过推一下就行。
泰勒推到这里,又想起了自己刚才那个问题:不一定非要从x=0的地方开始,也可以从((x_{0},f(x_{0})))开始。此时,只需要将0换成(x_{0}),然后再按照上面一模一样的过程重新来一遍,最后就能得到如下结果:
泰勒写到这里,长舒一口气,他写下结论:
有一条解析式很恶心的曲线(f(x)),我可以用多项式仿造一条曲线(g(x)),那么:
泰勒指出:在实际操作过程中,可根据精度要求选择n值,只要n不是正无穷,那么,一定要保留上式中的约等号。
若想去掉约等号,可写成下面形式:
好了,泰勒的故事讲完了。其实真正的数学推导只需要两步,困难的是不理解思想。如果背不过,就临时推导,只需要十几二十秒。
泰勒的故事讲完了,但是事情没完,因为泰勒没有告诉你,到底该求导几次。于是,剩下一帮人帮他擦屁股。
第一个帮他擦屁股的叫佩亚诺。他把上面式子中的省略号中的东西给整出来了。然而最终搁浅了,不太好用。
后面拉格朗日又跳出来帮佩亚诺擦屁股。至此故事大结局。
首先讲讲佩亚诺的故事。
简单回顾一下,上文提到,泰勒想通过一个多项式函数(g(x))的曲线,把那些看起来很恶心的函数(f(x))的曲线给仿造出来。提出了泰勒展开式,也就是下面的第一个式子:
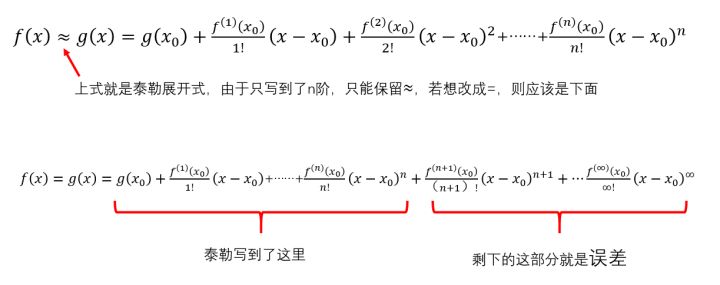
佩亚诺开始思考误差的事。先不说佩亚诺,假如让你思考这个问题,你会有一个怎样的思路?既然是误差,肯定越小越小对吧。所以当我们思考误差的时候,很自然的逻辑就是让这个误差趋近于0。
佩亚诺也是这么想的,他的大方向就是令后面这半部分近似等于0,一旦后半部分很接近0了,那么就可以省去了,只展开到n阶就可以了,泰勒展开就可以用了。但是他不知道如何做到。
后来,他又开始琢磨泰勒的整个思路:先保证初始点位置相同,再保证一阶导数相同,有点相似了,再保证二阶导数相同,更细化了,再保证三阶导数相同……突然灵光闪现:泰勒展开是逐步细化的过程,也就是说,每一项都比前面一项更加精细化(更小)。举个例子,你想把90斤粮食添到100斤,第一次,添了一大把,变成99斤了,第二次,添了一小把,变成99.9斤了,第三次,添了一小撮,变成99.99斤了……每一次抓的粮食,都比前一次抓的少。泰勒展开式里面也是这样的:

由此可见,最后一项(n阶)是最小的。皮亚诺心想:只要让总误差(后面的所有项的总和)比这一项还要小,不就可以把误差忽略了吗?
现在的任务就是比较大小,比较泰勒展开式中的最后一项、与误差项的大小,即:

如何比较大小?高中生都知道,比较大小无非就是作差或者坐商。不能确定的话,一个个试一下。最终,皮亚诺用的坐商。他用误差项除以泰勒展开中的最小的项,整理后得到:

红框内的部分是可以求出具体数字的。佩亚诺写到这里,偷了个懒,直接令 趋近于
,这样,误差项除以泰勒展开中的最小项不就趋近于0了吗?误差项不就趋近于0了吗?
我不知道你们看到这里是什么感觉,可能你觉得佩亚诺好棒,也可能觉得,这不糊弄人嘛。
反正,为了纪念佩亚诺的贡献,大家把上面的误差项成为佩亚诺余项。
总结一下佩亚诺的思路:首先,他把泰勒展开式中没有写出来的那些项补全,然后,他把这些项之和称为误差项,之后,他想把误差项变为0,考虑到泰勒展开式中的项越来越小,他就让误差项除以最后一项,试图得到0的结果,最后发现,只有当(x)趋近于(x_0)时,这个商才趋近于0,索性就这样了。
其实整体思路很简单,当初学不会,无非是因为数学语言描述这么个思路会让人很蒙逼。佩亚诺的故事讲完了,他本想完善泰勒展开,然而,他的成果只能算(x) 趋近于(x_0)时的情况。这时候,拉格朗日出场了。
拉格朗日的故事说来话长,从头说起吧。话说有一天,拉格朗日显得无聊,思考了一个特别简单的问题:一辆车,从(S_1)处走到(S_{2})处,中间用了时间(t),那么这辆车的平均速度就是(v=frac{S_{1}-S_{2}}{t}),假如有那么一个时刻,这辆车的瞬时速度是小于平均速度(v)的,那么,肯定有一个时刻,这辆车的速度是大于平均速度(v)的,由于车的速度不能突变,从小于(v)逐渐变到大于(v),肯定有一个瞬间是等于(v)的。
就这个问题,我相信在做的大多数,即使小时候没有听说过拉格朗日,也一定能想明白这个问题。
拉格朗日的牛逼之处在于,能把生活中的这种小事翻译成数学语言。他把(S-t)图像画出来了,高中生都知道,在这个图像中,斜率表征速度:
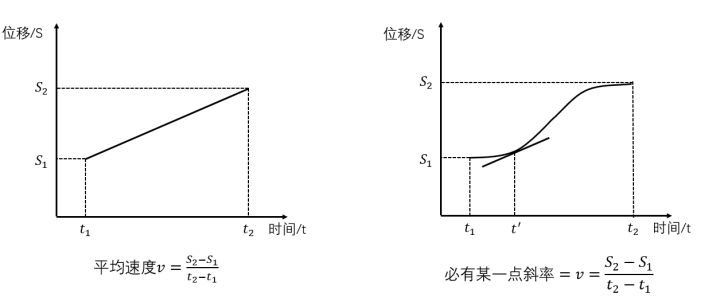
把上面的这个简单的问题用数学语言描述出来,就是那个被拉格朗日了的定理,简称拉格朗日中值定理:有个函数(S(t)),如果在一个范围内连续,可求导,则(frac{S(t_{2})-S(t_{1})}{t_{2}-t_{1}}=S^{'}(t^{'}))
后来啊,拉格朗日的中值定理被柯西看到了,柯西牛逼啊,天生对于算式敏感。柯西认为,纵坐标是横坐标的函数,那我也可以把横坐标写成一个函数啊,于是他提出了柯西中值定理:
拉格朗日听说了这事,心里愤愤不平,又觉得很可惜,明明是自己的思路,就差这么一步,就让柯西捡便宜了,不过柯西确实说的有道理。这件事给拉格朗日留下了很深的心理阴影。
接下来,拉格朗日开始思考泰勒级数的误差问题,他同佩亚诺一样,只考虑误差部分(见前文)。
插一句,各位老铁,接下来拉格朗日的操作绝壁开挂了,我实在是编不出来他的脑回路
首先,跟佩亚诺一样,先把误差项写出来,并设误差项为(R(x)):
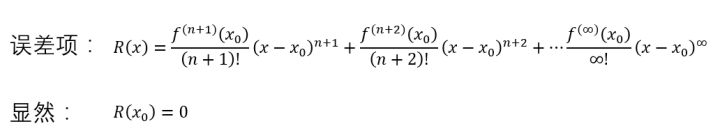
误差项(R(x))中每一项都是俩数的乘积,假如是你,你肯定是想两边同时除掉一个((x-x_{0})^{n+1}),对吧,为了简单,把((x-x_{0})^{n+1})设为(T(x)) :

所以除过之后,就成了:
(dfrac{R(x)}{T(x)}=dfrac{R(x)-0}{T(x)-0}=dfrac{R(x)-R(x_0)}{T(x)-T(x_0)})
等等,这一串东西看着怎么眼熟?咦?这不是柯西老哥推广的我的中值定理么?剩下的不就是……:
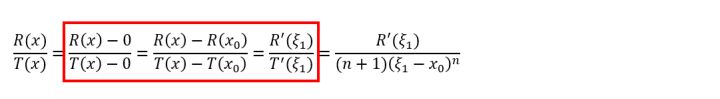
红框中,脑路之清奇、操作之风骚、画风之诡异、场面之震撼,让我们不禁感慨,拉格朗到底日了什么,脑海里才会想到柯西
拉格朗日写到这里卡住了,不知道你们有没有这种经验,反正我思考一道数学题的时候,会尝试着把思路进行到底,直到完全进了死胡同才会否定这种思路。有了前面的脑洞,拉格朗日继续复制这种思路,想看看能不能继续往下写:
先看分子
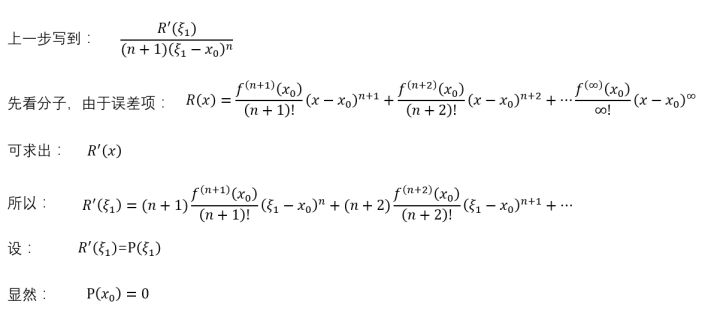
再看分母
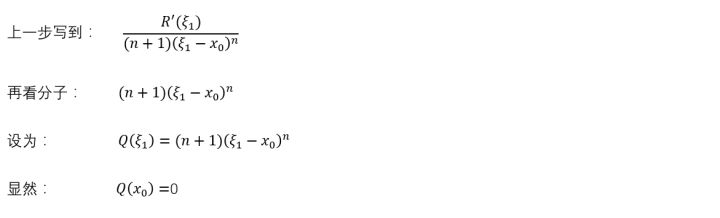
好巧合,又可以用一次柯西的中值定理了。
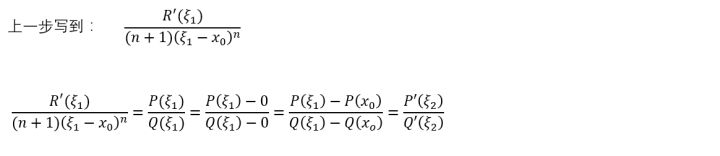
总之,按照这种方法,可以一直求解下去,最终的结果就是:
(误差项=dfrac{f^{n+1}(zeta)}{(n+1)!}(x-x_0)^{n+1})
至此,拉格朗日把后面无数多的误差项给整合成了一项,而且比配诺亚更加先进的地方在于,不一定非要让(x)趋近于 (x_0),可以在二者之间的任何一个位置(zeta)处展开,及其好用。
本文涵盖泰勒展开式、佩亚诺余项、拉格朗日中值定理、柯西中值定理、拉格朗日余项。全文完毕。
结束!!!
Reference
作者:退乎
链接:https://www.zhihu.com/question/25627482/answer/313088784
来源:知乎