回溯算法介绍
回溯算法可以搜索一个问题的所有解,本质是用递归代替N层for循环来“暴力穷举”
原理如下:
- 从根节点出发深度搜索解空间树
- 搜索到有解的分支时,继续向下搜索
- 搜索到无解的分支时,回退到上一步,顾名思义“回溯”
框架套路
talk is cheap,show you the 套路,框架如下
结果集=[]
function dfs(选择列表,已选择的数组)
if 结束条件
结果集追加
return
for 选择 in 选择列表
做选择
dfs(选择列表, 已选择数组) 进入下一次选择
取消选择
dfs(选择列表,[])
return 结果集
思路来自labuladong的算法小抄,自己改成了个人觉得更通用的版本,默认收集所有的解,便于跟踪调试。
重点:
- 选择列表。当前可以做出的选择
- 已选择路径。已经做出的选择
- 结束条件。无法再做出选择的条件
有了这框架,以后遇到需要穷举的算法,把3个重点想通,直接套用,简直不要太嗨~
算法示例
以下算法全用python实现,需要注意的是python的数组默认是传递引用,引入了copy包来复制数组
全组合
全组合是穷举的代表了吧,给定指定不重复的字符串,比如给定["a","b"],返回所有的组合结果应该是
aa
ab
ba
bb
我们来套用框架实现一下,代码如下
import copy
# 全组合
def combination(str_list):
res = []
max_len = len(str_list)
def dfs(str_list, track_list):
if len(track_list) == max_len: # 满足条件,加入结果集
res.append(track_list)
return
for c in str_list:
track_list.append(c) # 选择
dfs(str_list, copy.copy(track_list)) # 进入下一次选择
track_list.pop() # 取消选择
dfs(str_list, [])
return res
三个重点:
- 选择列表。可以选择的字符串,比如['a','b','c'],对应变量str_list。
- 已选择路径。已经做出的选择,比如已经选择了['a'],对应变量track_list。
- 结束条件。无法再做出选择的条件,已选择的数组长度等于最大长度,对应
len(track_list) == max_len。
我们来测试一下
for v in combination(['a', 'b']):
print(v)
运行输出

全排列
全排列和全组合差不多,唯一的区别是已经选择过的字符串,不让选择了。
我们只需要在全组合代码的基础上加上限制即可,代码如下
import copy
# 全排列
def permute(str_list):
res = []
max_len = len(str_list)
def dfs(str_list, track_list):
if len(track_list) == max_len: # 满足条件,加入结果集
res.append(track_list)
return
for c in str_list:
if c in track_list: # 已经存在的不再添加
continue
track_list.append(c) # 选择
dfs(str_list, copy.copy(track_list)) # 进入下一次选择
track_list.pop() # 取消选择
dfs(str_list, [])
return res
我们只是改了一下这里
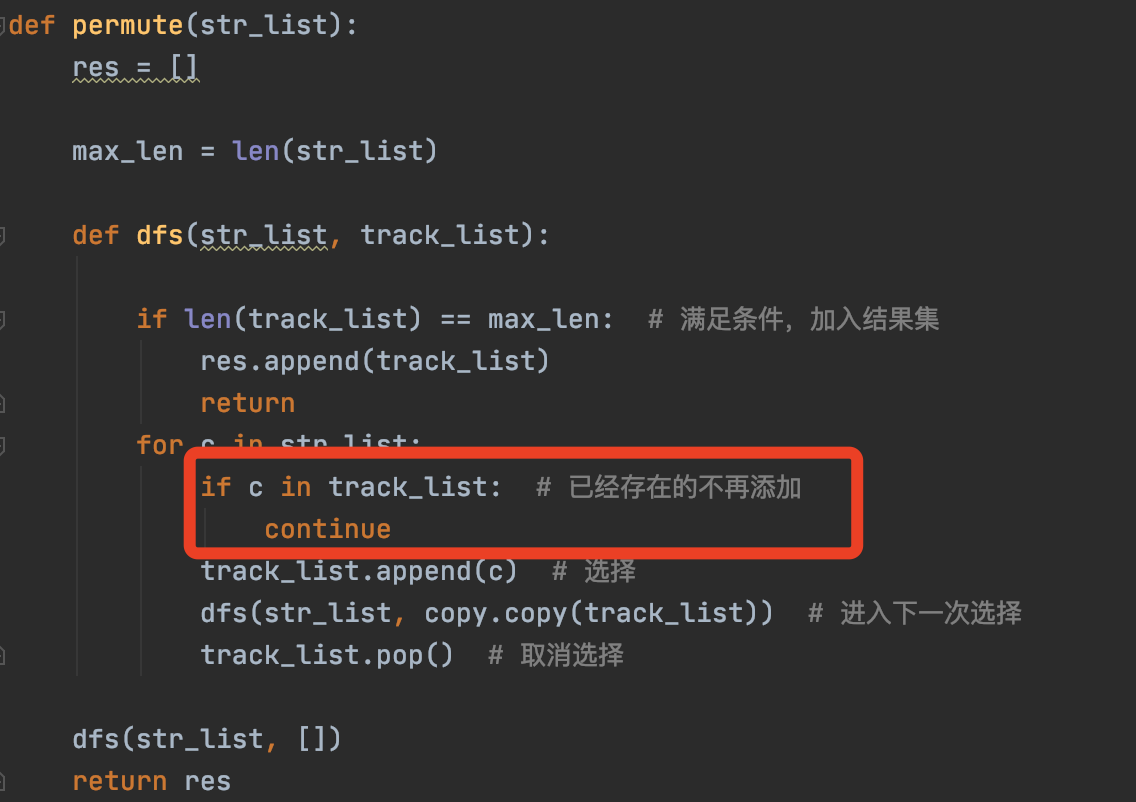
我们用chenqionghe的简称['c','q','h']来测试一下
for v in permute(['c', 'q', 'h']):
print(v)
运行输出

凑零钱
给定数量N种面值的硬币, 再给定一个金额,返回硬币凑出这个金额的最少数量。
比如,给定硬币1, 2, 5,总额为10,最少需要2枚硬币5+5=10
代码实现如下
def coin_change(coins, amount):
res_list = []
def dfs(n, track_list):
if n == 0:
res_list.append(track_list) # 满足条件
return 0
if n < 0:
return -1
for coin in coins:
track_list.append(coin) # 做选择
dfs(n - coin, copy.copy(track_list)) # 选择一个硬币,目标金额就会减少,解变为1+sub
track_list.pop() # 取消选择
dfs(amount, [])
return res_list
三个重点:
- 选择列表。可以选择的硬币,对应coins数组。
- 已选择路径。已经做出的选择,对应track_list数组。
- 结束条件。无法再做出选择的条件,金额为0和负的时候。
需要注意的是:df函数代表的是:目标金额是n,需要dfs[n]个硬币,比如给定金额10,这次选择了2,这次选择能达到的金额数量是1+dfs(10 - 2),也就是1+dfs(8)
我们来运行一下:
for v in coin_change([2, 3, 5], 10):
print(v)
输出如下
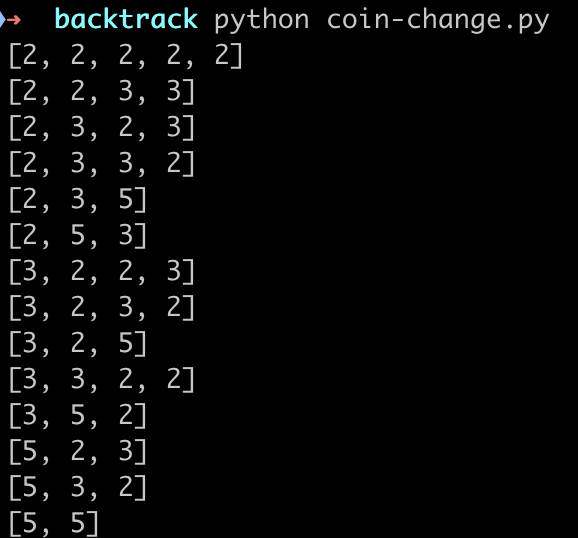
给出了所有的方案,如果要最小的硬币只需要统计长度最小的即可。
N皇后
最典型的是八皇后:
在8×8格的国际象棋上摆放8个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上,问有多少种摆法。
以4皇后为例,给定数字4,应该给出两种方案如下
第一种方案
. Q . .
. . . Q
Q . . .
. . Q .
第二种方案
. . Q .
Q . . .
. . . Q
. Q . .
套用框架实现如下
# N皇后问题
def solve_n_queens(n):
res = []
def dfs(board, row):
if row == n: # 到达最后一行,追加结果集
res.append(board)
for col in range(n):
# 排除不合法的选择
if not is_valid(board, row, col, n):
continue
board[row][col] = 'Q' # 选择第row行第col列放Q
dfs(copy.deepcopy(board), row + 1)
board[row][col] = '.' # 撤销选择
return False
board = [['.'] * n for _ in range(n)] # 初始化二维数组
dfs(board, 0) # 从第0行开始做选择
return res
# 判断是否能在board[row][col]放置Q
def is_valid(board, row, col, n):
# 垂直方向是否有Q
for v in range(row):
if board[v][col] == 'Q':
return False
# 左上方是否有Q
i, j = row - 1, col - 1
while i >= 0 and j >= 0:
if board[i][j] == 'Q':
return False
i = i - 1
j = j - 1
# 右上方是否有Q
i, j = row - 1, col + 1
while i >= 0 and j <= n - 1:
if board[i][j] == 'Q':
return False
i = i - 1
j = j + 1
return True
N皇后的解法是,在每行做选择,选择为N列,做出选择后,进入下一行继续做选择
三个重点:
- 选择列表。可以选择的列,对应的是0-n的任意一列。
- 已选择路径。已经做出的选择,对应board二维数组。
- 结束条件。无法再做出选择的条件,也就是已经到达最后一行的时候。
注意:is_valid的函数,主要是判断检测当前位置是否能放“皇后”,也就是检查垂直、左上方向和右上方是不是都没有“皇后”
我们来测试一下
res = solve_n_queens(8)
for data in res:
print('-' * 20)
for v in data:
print(" ".join(v))
运行输出如下

最长递增子序列
给定一个未排序的整数数组,求这个数组的最长递增子序列
例如
输入: [10,9,2,5,3,7,101,18]
输出: 4
解释: 最长递增子序列是 [2,3,7,101], 所以长度为 4.
下面用回溯框架实现一下,找出所有的递增序列和最大的序列
import copy
def long_increasing_subsequence(arr):
res_list = []
n = len(arr)
max_len = 1
max_sub = []
# 从第i个元素做选择
def dfs(i, track_list):
# 到达末尾 或 下一个元素比track数组最后一个大
if i == n or (len(track_list) > 0 and arr[i] < track_list[-1]):
res_list.append(track_list) # 满足条件
nonlocal max_len, max_sub
if max_len < len(track_list):
max_len = len(track_list)
max_sub = track_list
return
for v in range(i, n):
if len(track_list) > 0 and arr[v] < track_list[-1]:
continue
track_list.append(a[v]) # 做选择
if v < n:
dfs(v + 1, copy.copy(track_list)) # 下一次选择
track_list.pop() # 取消选择
dfs(0, [])
return max_sub, res_list
a = [10, 9, 2, 5, 3, 7, 101, 18]
max_sub, res_list = long_increasing_subsequence(a)
print(max_sub)
运行输出如下

最长公共子序列
给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。
例如
输入:text1 = "abcde", text2 = "ace"
输出:3
解释:最长公共子序列是 "ace",它的长度为 3。
下面用回溯框架实现一下,找出所有的公共子序列。
这次不太一样,因为之前都只有一个选择数组,这次变成了两个
import copy
def long_common_subsequence_all(str1, str2):
len1, len2 = len(str1), len(str2)
res_list = []
def dp(i, j, track1, track2):
if i == len1 or j == len2:
# 到头了,收集一下,相同的子序列
res_list.append("".join(track1))
return
c_track1 = copy.copy(track1)
c_track2 = copy.copy(track2)
if str1[i] == str2[j]:
# 找到一个lcs中的元素,str1和str2分别选中,继续往下找
c_track1.append(str1[i])
c_track2.append(str2[j])
dp(i + 1, j + 1, c_track1, c_track2)
return
else:
dp(i, j + 1, c_track1, c_track2)
dp(i + 1, j, c_track1, c_track2)
dp(0, 0, [], [])
lcs = ""
for cs in res_list:
if len(cs) > len(lcs):
lcs = cs
return lcs, res_list
s1 = "abcde"
s2 = "ace"
lcs, res_list = long_common_subsequence_all(s1, s2)
print(lcs)
优化思路
备忘录避免重复计算
以凑零钱为例,里边其实会出现很多相同子问题的递归
以10举个例子,当我们选择了选择了[2, 3]和[5]的时候,都需要再计算dfs(5)的值。数据越大,重复的递归越多,性能越差。
我们可以引入一个map,记录已经计算出的值,下次遇到相同问题直接返回结果
def coin_change_optimization(coins, amount):
memo = {}
def dfs(n):
if n in memo:
return memo[n]
if n == 0:
return 0
if n < 0:
return -1
min_res = float('INF')
for coin in coins:
sub = dfs(n - coin) # 选择一个硬币,目标金额就会减少,解变为1+sub
if sub == -1:
continue
if min_res > 1 + sub: # 更新最小值
min_res = 1 + sub
memo[n] = min_res if min_res != float('INF') else -1
return memo[n]
return dfs(amount)
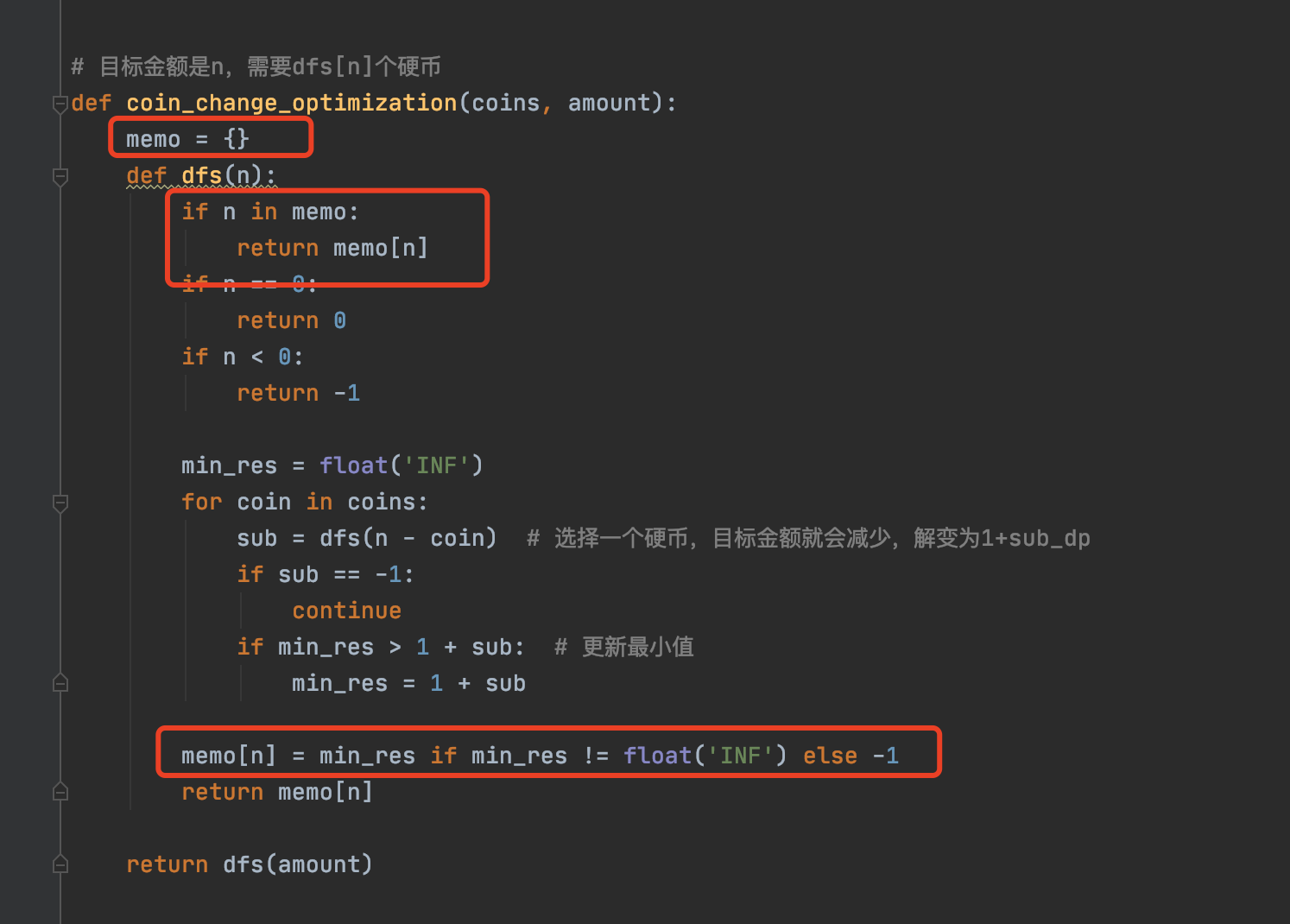
向上返回阻断其他递归
以N皇后为例,我们只需要在得到解的时候return,并在上层接收即可,代码如下
# N皇后问题
def solve_n_queens(n):
res = []
def dfs(board, row):
if row == n: # 到达最后一行,追加结果集
res.append(board)
return True
for col in range(n):
# 排除不合法的选择
if not is_valid(board, row, col, n):
continue
board[row][col] = 'Q' # 选择第row行第col列放Q
if dfs(copy.deepcopy(board), row + 1):
return True
board[row][col] = '.' # 撤销选择
return False
board = [['.'] * n for _ in range(n)] # 初始化二维数组
dfs(board, 0) # 从第0行开始做选择
return res
以上只是在这里做了改动

看到没有,这就是回溯暴力穷举的艺术,最简单的框架,解决最难的问题~