第4章变换4.2特殊矩阵变换和运算

4.2 特殊矩阵变换和运算

在本节中，将介绍和导出对实时图形必不可少的几个矩阵变换和运算。首先，我们介绍了欧拉变换（连同它的参数提取），这是一种描述方向的直观方式。然后我们谈到从单个矩阵中反演一组基本变换。最后，导出了一种方法，可以绕任意轴旋转实体。

4.2.1 欧拉变换

此变换是构建矩阵，以将你自己（即相机）或任何其他实体定向到某个方向的直观方式。它的名字来源于伟大的瑞士数学家莱昂哈德·欧拉（Leonhard Euler，1707-1783）。

首先，必须建立某种默认的视图方向。大多数情况下，它朝向负z轴，头部沿y轴定向，如图4.7所示。欧拉变换是三个矩阵的相乘，即图中所示的旋转。更正式地，表示为\(\textbf{E}\)的变换由公式4.21给出：

\[{\textbf{E}}(h,p,r) = {\textbf{R}}_z(r){\textbf{R}}_x (p){\textbf{R}}_y(h) \tag{4.21} \]

矩阵的顺序可以以24种不同的方式进行选择[1636]；我们介绍这个是因为它很常用。由于\(\textbf{E}\)是旋转矩阵的级联，因此它显然也是正交的。因此，它的逆可以表示为\({\textbf{E}}^{-1} = {\textbf{E}}^{T} = ({\textbf{R}}_z{\textbf{R}}_x{\textbf{R}}_y)^T = {\textbf{R}}^T_y{\textbf{R}}^T_x{\textbf{R}}^T_z\)，当然，尽管直接使用\(\textbf{E}\)的转置更容易。

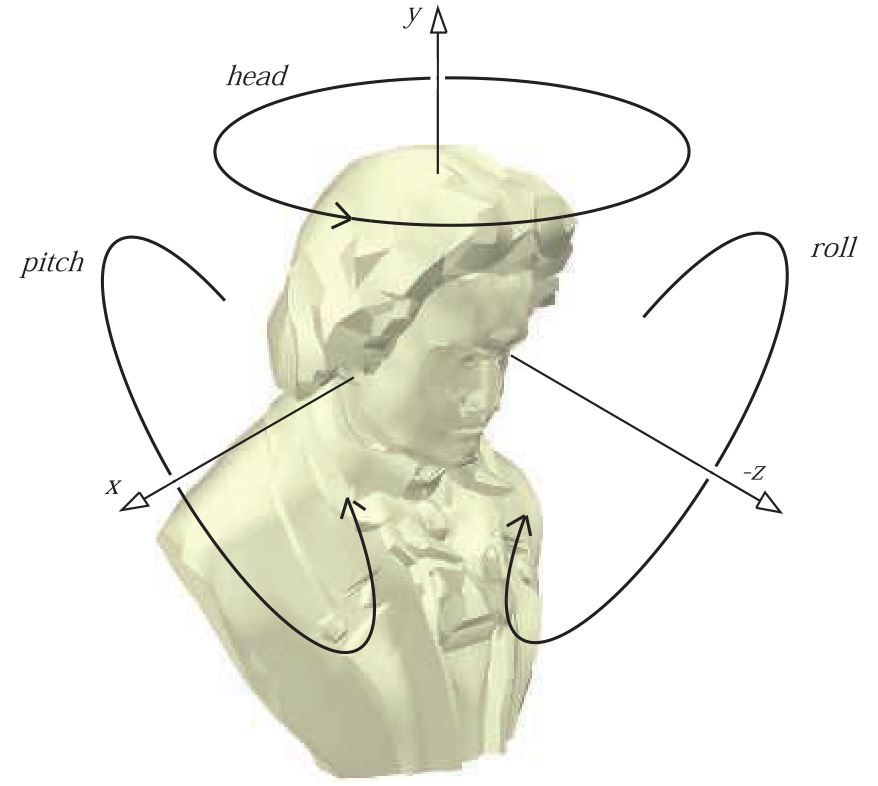
图4.7. 欧拉变换，以及它如何与你改变航向、俯仰和滚动角度的方式相关联。显示默认视图方向，沿负z轴朝向，沿y轴向上方向。

欧拉角\(h\)、\(p\)和\(r\)表示航向、俯仰和滚转应围绕各自的轴旋转的顺序和程度。有时这些角度都被称为“滚动”，例如，我们的“航向”是“y-roll”，我们的“俯仰”是“x-roll”。 此外，“航向”有时也称为“偏航”，例如在飞行模拟中。

这种转换是直观的，因此很容易用外行的语言进行讨论。例如，改变航向角使观看者摇头“不”，改变俯仰角使他们点头，而改变滚动角度使他们将头侧向倾斜。我们不讨论围绕x轴、y轴和z轴的旋转，而是讨论改变航向、俯仰和滚动。请注意，此变换不仅可以定向相机，还可以定向任何对象或实体。可以使用世界空间的全局轴或相对于局部参考系来执行这些变换。

重要的是要注意，欧拉角的一些表示将z轴作为初始向上方向。这种差异纯粹是一种符号变化，尽管可能会令人困惑。在计算机图形学中，在如何看待世界以及如何形成内容方面存在分歧：y-up或z-up。大多数制造过程，包括3D打印，都认为z方向在世界空间中；航空和海上交通工具认为-z向上。建筑和GIS通常使用z-up，因为建筑平面图或地图是二维的，x和y。与媒体相关的建模系统通常将y方向视为世界坐标中的向上，这与我们在计算机图形中始终描述相机屏幕向上方向的方式相匹配。这两个坐标系向上向量选择之间的区别只是90度旋转（可能还有一个反射），但不知道假设哪个会导致问题。在本卷中，除非另有说明，否则我们使用y-up的世界方向。

我们还想指出，相机在其视图空间中的向上方向与世界的向上方向没有特别的关系。转动你的头，视图是倾斜的，它的世界空间向上方向与世界不同。再举一个例子，假设世界使用y-up，我们的相机直视下方的地形，鸟瞰图。这个方向意味着相机向前倾斜了90度，因此它在世界空间中的向上方向是\((0,0,-1)\)。在这个方向上，相机没有y分量，而是认为-z在世界空间中是向上的，但根据定义，“y是向上”在视图空间中仍然是正确的。

虽然对于小角度变化或观察者定向很有用，但欧拉角还有一些其他严重的限制。很难将两组欧拉角组合使用。例如，一组和另一组之间的插值并不是对每个角度进行插值的简单问题。事实上，两组不同的欧拉角可以给出相同的方向，因此任何插值都不应该旋转对象。这些是使用替代方向表示（如本章稍后讨论的四元数）值得研究的一些原因。使用欧拉角，你还遇到被称为万向节死锁的问题，这将在接下来的第4.2.2节中解释。

4.2.2 从欧拉变换中提取参数

在某些情况下，从正交矩阵中提取欧拉参数\(h\)、\(p\)和\(r\)的过程很有用。此过程如公式4.22所示：

\[{\textbf{E}}(h,p,r) = \left( \begin{matrix} e_{00} & e_{01} & e_{02} \\ e_{10} & e_{11} & e_{12} \\ e_{20} & e_{21} & e_{22} \end{matrix} \right) = {\textbf{R}}_z(r){\textbf{R}}_x(p){\textbf{R}}_y(h) \tag{4.22} \]

在这里，我们放弃了\(4×4\)矩阵，改为\(3×3\)矩阵，因为后者提供了旋转矩阵的所有必要信息。也就是说，等效的\(4×4\)矩阵的其余部分总是在右下角位置包含0和1。

将方程4.22中的三个旋转矩阵连接起来得到:

\[{\textbf{E}} = \left( \begin{matrix} {\rm{cos}}r\ {\rm{cos}}h - {\rm{sin}}r\ {\rm{sin}}p\ {\rm{sin}}h & -{\rm{sin}}r\ {\rm{cos}}p & {\rm{cos}}r\ {\rm{sin}}h + {\rm{sin}}r\ {\rm{sin}}p\ {\rm{cos}}h \\ {\rm{sin}}r\ {\rm{cos}}h + {\rm{cos}}r\ {\rm{sin}}p\ {\rm{sin}}h & {\rm{cos}}r\ {\rm{cos}}p & {\rm{sin}}r\ {\rm{sin}}h - {\rm{cos}}r\ {\rm{sin}}p\ {\rm{cos}}h \\ -{\rm{cos}}p\ {\rm{sin}}h & {\rm{sin}}p & {\rm{cos}}p\ {\rm{cos}}h \end{matrix} \right) \tag{4.23} \]

显而易见，俯仰角参数由\({\rm{sin}}p=e_{21}\)给出。此外，将\(e_{01}\)除以\(e_{11}\)，类似地将\(e_{20}\)除以\(e_{22}\)，得到以下航向角和翻滚角参数的提取方程：

\[\frac{e_{01}}{e_{11}} = \frac{-{\rm{sin}}r}{{\rm{cos}}r} = -{\rm{tan}}r \quad {\rm{and}} \quad \frac{e_{20}}{e_{22}} = \frac{-{\rm{sin}}h}{{\rm{cos}}h} = -{\rm{tan}}h \tag{4.24} \]

因此，使用函数\(\rm{atan2}(y,x)\)（参见第1章的第8页）从矩阵\(\textbf{E}\)中提取欧拉参数\(h\)（航向）、\(p\)（俯仰）和\(r\)（滚动），如公式4.25所示：

\[ \begin{aligned} h &= {\rm{atan2}}(−e_{20}, e_{22})\\ p &= {\rm{arcsin}}(e_{21}) \\ r &= {\rm{atan2}}(−e_{01}, e_{11}) \end{aligned} \tag{4.25} \]

但是，我们需要处理一个特殊情况。如果\({\rm{cos}}p = 0\)，我们会遇到万向节死锁的问题（第4.2.2节）：旋转角\(r\)和\(h\)将围绕同一轴旋转（尽管可能在不同的方向上，取决于\(p\)旋转角是\(-\pi/2\)还是\(\pi/2\))，所以只需要推导出一个角度。如果我们任意设置\(h = 0\)[1769]，我们得到

\[{\textbf{E}} = \left( \begin{matrix} {\rm{cos}}r & -{\rm{sin}}r\ {\rm{cos}}p & {\rm{sin}}r\ {\rm{sin}}p \\ {\rm{sin}}r & {\rm{cos}}r\ {\rm{cos}}p & -{\rm{cos}}r\ {\rm{sin}}p \\ 0 & {\rm{sin}}p & {\rm{cos}}p \end{matrix} \right) \tag{4.26} \]

因为\(p\)不影响第一列中的值，当\({\rm{cos}}p = 0\)时我们可以使用\({\rm{sin}}r/{\rm{cos}}r = {\rm{tan}}r = e_{10} /e_{00}\)，可给出\(r = {\rm{atan2}}(e_{10} ,e_{00})\)。

注意，从arcsin的定义来看，\(-π/2 ≤ p ≤ π/2\)，这意味着如果\(\textbf{E}\)是用超出这个区间的p值创建的，则无法提取原始参数。\(h\)、\(p\) 和\(r\)不是唯一的，这意味着可以使用一组以上的欧拉参数来产生相同的变换。更多关于欧拉角转换的信息可以在Shoemake在1994年的文章[1636] 中找到。上面概述的简单方法可能会导致数值不稳定的问题，这是可以避免的，但会降低速度[1362]。

当您使用欧拉变换时，可能会产生称为万向节死锁的问题[499,1633]。当进行旋转从而失去一个自由度时，就会发生这种情况。例如，假设变换的顺序是x/y/z。考虑仅围绕y轴旋转π/2，进行第二次旋转。这样做会旋转局部z轴以与原始x轴对齐，因此围绕z的最终旋转是多余的。

在数学上，我们已经在公式4.26中看到了万向死节锁，其中我们假设\({\rm{cos}}p = 0\)，即\(p = ±π/2 + 2πk\)，其中\(k\)是一个整数。有了这样的\(p\)值，我们失去了一个自由度，因为矩阵只取决于一个角度，\(r + h\)或\(r − h\)（但不能同时取决于两者）。

虽然欧拉角在建模系统中通常呈现为\(x/y/z\)顺序，但围绕每个局部轴旋转，其他排序也是可行的。例如，\(z/x/y\)用于动画，而\(z/x/z\)用于动画和物理。所有这些都是指定三个独立旋转的有效方法。最后一个顺序，z/x/z，对于某些应用来说可能更好，因为只有当围绕x轴旋转\(\pi\)弧度（半旋转）时才会发生万向节死锁。没有完美的序列可以避免万向节死锁。尽管如此，欧拉角还是常用的，因为动画师更喜欢曲线编辑器来指定角度如何随时间变化 [499]。

示例：约束一个变换。想象一下，你正握着一个（虚拟）扳手正夹住螺栓。要将螺栓固定到位，您必须围绕x轴旋转扳手。现在假设您的输入设备（鼠标、VR手套、太空球等）为你提供了一个旋转矩阵，即用于扳手移动的旋转。问题是将这个变换应用到扳手可能是错误的，它应该只围绕x轴旋转。要将称为\(\textbf{P}\)的输入变换限制为绕x轴旋转，只需使用本节中描述的方法提取欧拉角\(h\)、\(p\) 和\(r\)，然后创建一个新矩阵\(\textbf{R}_x(p)\)。这就是广受欢迎的变换，它将围绕x轴旋转扳手（如果\(\textbf{P}\)现在包含这样的运动）。

4.2.3 矩阵分解

到目前为止，我们一直在假设我们知道我们正在使用的转换矩阵的起来和过程。通常情况并非如此。例如，可能与某个变换对象关联的只不过是一个级联矩阵。从级联矩阵中反推各种变换的任务称为矩阵分解。

反推一组转换的原因有很多。用途包括：

• 仅提取对象的缩放因子。
• 查找特定系统所需的转换。（例如，某些系统可能不允许使用任意\(4×4\)矩阵。）
• 确定模型是否仅经历了刚体变换。
• 在只有对象矩阵可用的动画中的关键帧之间进行插值。
• 从旋转矩阵中移除剪切。

我们已经介绍了两种分解，即为刚体变换导出平移和旋转矩阵（第4.1.6节）和从正交矩阵导出欧拉角（第4.2.2节）。

正如我们所见，反推平移矩阵很简单，因为我们只需要\(4×4\)矩阵的最后一列中的元素。我们还可以通过检查矩阵的行列式是否为负来确定是否发生了反射。分离出旋转、缩放和剪切需要进行更多的工作。

幸运的是，有几篇关于这个主题的文章，以及在线可用的代码。Thomas[1769]和Goldman[552,553]各自提出了不同类别的转换方法。Shoemake[1635]改进了他们的仿射矩阵技术，因为他的算法独立于参考系，并尝试分解矩阵以获得刚体变换。

4.2.4 绕任意轴旋转

有时，将实体绕任意轴旋转某个角度的过程是很方便的。假设旋转轴\(\textbf{r}\)已正则化，并且创建了一个围绕\(\pmb{r}\)旋转\(\alpha\)弧度的变换。

为此，我们首先变换到一个空间，其中我们想要旋转的轴是x轴。这是通过一个称为\(\textbf{M}\)的旋转矩阵完成的。然后执行实际的旋转，我们使用\(\textbf{M}^{-1}\)[314]变换回来。 此过程如图4.8所示。

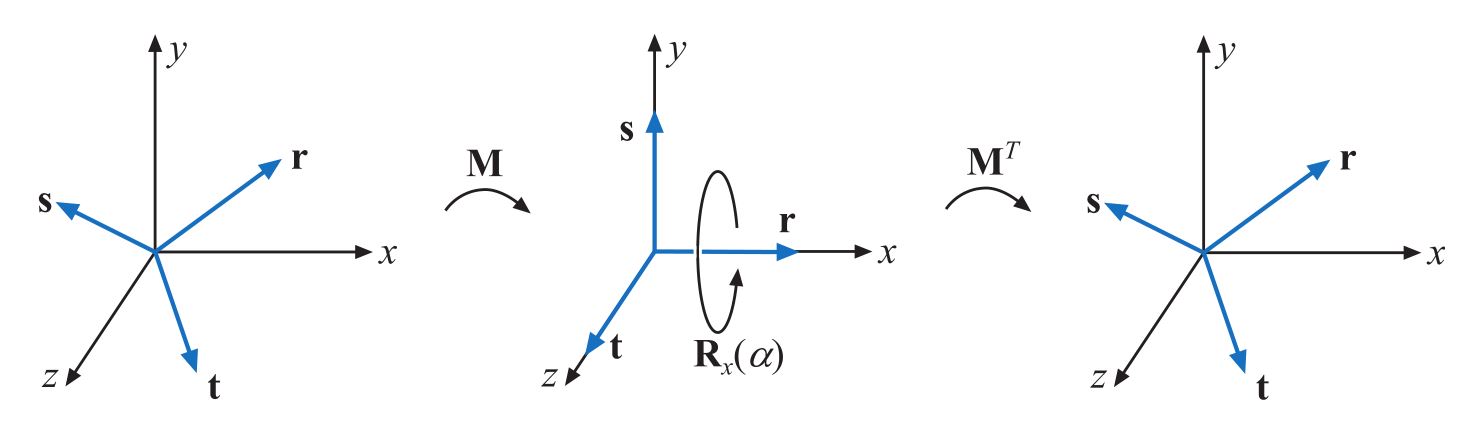
图4.8. 绕任意轴\(\textbf{r}\)的旋转是通过找到由\(\textbf{r}\)、\(\textbf{s}\)和\(\textbf{t}\)形成的标准正交基来完成的。然后我们将此基与标准基对齐，以便\(\textbf{r}\)与x轴对齐。在这个标准基中进行绕x轴的旋转，最后我们变换回原来的坐标基。

为了计算\({\textbf{M}}\)，我们需要找到两个与\(\textbf{r}\)和彼此正交的轴。我们专注于找到第二个轴\(\textbf{s}\)，因为第三个轴\(\textbf{t}\)将是第一个和第二个轴的叉积：\(\textbf{t} = \pmb{r} × \pmb{s}\)。一个数值稳定的方法是找到\({\textbf{r}}\)的最小分量（绝对值），并将其设置为0。交换剩余的两个分量，然后取反第一个（实际上，任何一个非零分量都可以取反）。在数学上，这表示为[784]：

\[ \begin{split} \overline{\textbf{s}} = \begin{cases} (0, -r_z, r_y),\quad \rm{if}\, |r_x|\leq|r_y| \, \rm{and}\, |r_x|\leq|r_z|\\ (-r_z, 0, r_x),\quad \rm{if}\, |r_y|\leq|r_x| \, \rm{and}\, |r_y|\leq|r_z|\\ (-r_y, r_x, 0),\quad \rm{if}\, |r_z|\leq|r_x| \, \rm{and}\, |r_z|\leq|r_y| \end{cases} \\ \textbf{s} = \overline{\pmb{s}} / ||\overline{\pmb{s}}|| \\ \textbf{t} = \textbf{r} × \textbf{s} \end{split} \tag{4.27} \]

这保证\(\overline{\textbf{s}}\)与\(\textbf{r}\)正交（垂直），并且\((\textbf{r},\pmb{s},\pmb{t})\)是正交基。Frisvad[496]提出了一种代码中没有任何分支的方法，该方法速度更快但精度较低。Max[1147]和Duff等人[388]提高了Frisvad方法的准确性。无论采用哪种技术，这三个向量都用于创建旋转矩阵：

\[\textbf{M} = \left( \begin{matrix} {\textbf{r}}^T\\ {\textbf{s}}^T\\ {\textbf{t}}^T \end{matrix} \right) \tag{4.28} \]

该矩阵将向量\(\textbf{r}\)转换为x 轴，将\(\textbf{s}\)转换为y轴，将\(\textbf{t}\)转换为z轴。因此，围绕归一化向量\(\textbf{r}\)旋转\(\alpha\)弧度的最终变换是:

\[{\textbf{X}} = {\textbf{M}}^{T}{\textbf{R}}_x(\alpha){\textbf{M}} \tag{4.29} \]

换句话说，这意味着首先我们变换使得\(\textbf{r}\)是x轴（使用\({\textbf{M}}\)），然后我们围绕这个x轴旋转\(\alpha\)个弧度（使用\({\textbf{R}}_x(\alpha)\)），然后我们使用\({\textbf{M}}\)的逆，在这种情况下是\({\textbf{M}}^{T}\)，因为\({\textbf{M}}\)是正交的。

Goldman[550]提出了另一种绕任意标准化轴\(\textbf{r}\)旋转\(\phi\)弧度的方法。在这里，我们简单介绍一下他的变换：

\[{\textbf{R}} = \left( \begin{matrix} {\rm{cos}}{\phi} + (1−{\rm{cos}}{\phi})r_x^2 & (1−{\rm{cos}}{\phi})r_xr_y −r_z{\rm{sin}}{\phi} & (1−{\rm{cos}}{\phi})r_xr_z +r_y{\rm{sin}}{\phi}\\ (1−{\rm{cos}}{\phi})r_xr_y +r_z {\rm{sin}}{\phi} & {\rm{cos}}{\phi} + (1−{\rm{cos}}{\phi})r_y^2 & (1−{\rm{cos}}{\phi})r_yr_z − r_x{\rm{sin}}{\phi}\\ (1−{\rm{cos}}{\phi})r_xr_z − r_y{\rm{sin}}{\phi} & (1−{\rm{cos}}{\phi})r_yr_z + r_x{\rm{sin}}{\phi} & {\rm{cos}}{\phi} + (1−{\rm{cos}}{\phi})r_z^2 \end{matrix} \right) \tag{4.30} \]

在4.3.2节中，我们提出了另一种解决这个问题的方法，使用四元数。在该部分中还有针对相关问题的更有效算法，例如从一个向量到另一个向量的旋转。