多对多关系。顶点的有穷非空集合和顶点之间边的集合构成,表示为G(V, E)。
数据元素在线性表中叫元素、树中叫结点、图中叫顶点vertex。边无方向称为无向边,用无序偶(Vi, Vj)来表示。有向边(也称为弧)用有序偶<Vi, Vj>来表示。<弧尾,弧头>
基础概念
简单图:不存在顶点到自身的边,且一条边不重复出现。
无向完全图:任意两个顶点之间都存在边的无向图。n个顶点的无向完全图有n(n-1)/2条边。
有向完全图:任意两个顶点之间都存在两条弧的有向图。n个顶点的有向完全图有n(n-1)条边。
稀疏图和稠密图:边或弧数小于nlogn的图为稀疏图,反之为稠密图。
网:边或弧带权的图。
子图:顶点和边都为子集。
无向图顶点的度:和顶点相关联的边的数目。
有向图顶点的入度和出度:以顶点为头的弧的数目成为入度,以顶点为尾的弧的数目成为出度。度=入度+出度。
简单路径:顶点不重复的路径。
连通图:两个顶点之间有路径则是连通的,如果图中任意两个顶点都连通,就是连通图。
连通分量:无向图中的极大连通子图称为连通分量。
有向图中,如果任意一对顶点之间都存在路径,则称为强连通图。
有向图中的极大强连通子图称为有向图的强连通分量。
连通图的生成树:一个极小的连通子图,含有图中全部的n个顶点,但只有足以构成一棵树的n-1条边。
如果一个有向图恰有一个顶点入度为0,其余顶点的入度均为1,那么就是一颗有向树。
图的存储结构
无法以数据元素在内存中的物理位置来表示元素之间的关系(内存物理关系是线性的,图的关系是平面的)。
如果各个顶点度数相差太大,纯粹用多种链表导致无法想象的浪费。
五种不同的存储结构,特别是邻接矩阵和邻接表。
1. 邻接矩阵
一维数组存储顶点(因为顶点不分大小主次);边或弧用二维数组表示。无向图的邻接矩阵是对称的,浪费了一半空间。

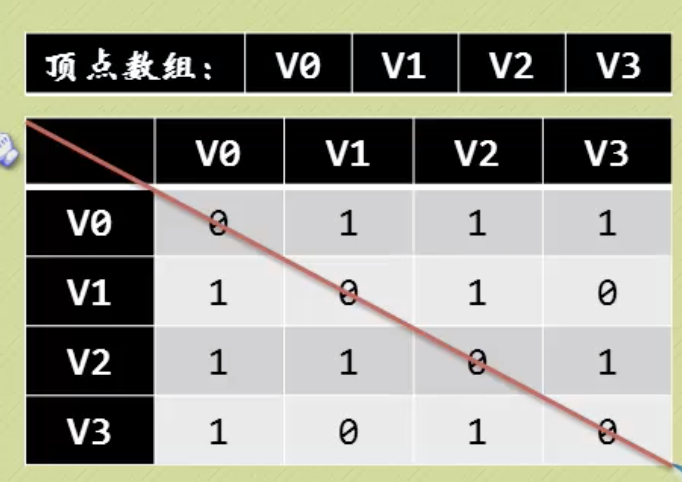
有向图的邻接矩阵不一定对称,顶点的入度是对应列不为0的个数之和,出度是对应行的。没有浪费空间,因为一定要区分弧的方向。
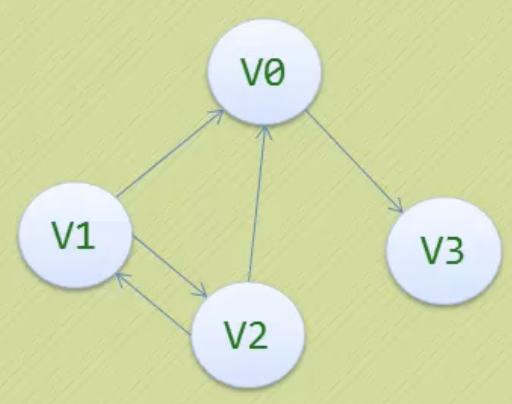
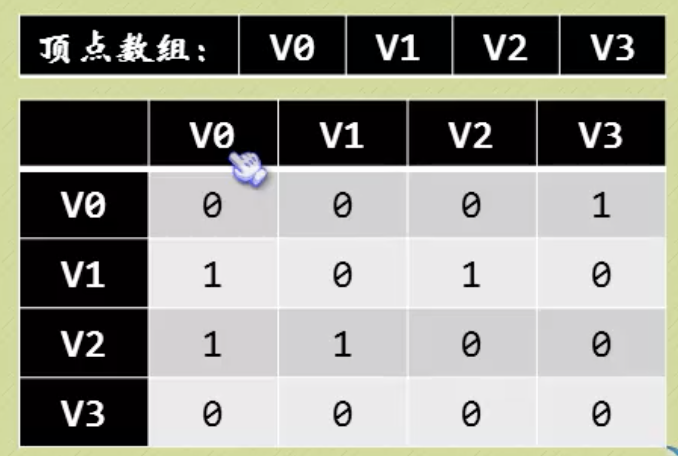
网的邻接矩阵,对应位置的取值是对应弧的权值,不存在的弧可以用一个计算机允许的、大于所有边上权值的值来表示。
2. 邻接表
边数相对于顶点较少的图,用邻接矩阵也很浪费空间。这时可以用邻接表,数组+链表。还是一维数组,但存的是顶点和指向该节点的第一个邻接点的指针,每个顶点的所有邻接点构成一个线性表,由于邻接点的个数不定,选择用单链表来存储。


对于有向图,顶点当弧尾建立邻接表,得到的是每个顶点的出度。(入度的话是顶点当弧头;逆邻接表)。

对于网,可以在边表结点的定义中再加一个数据域来存储权。
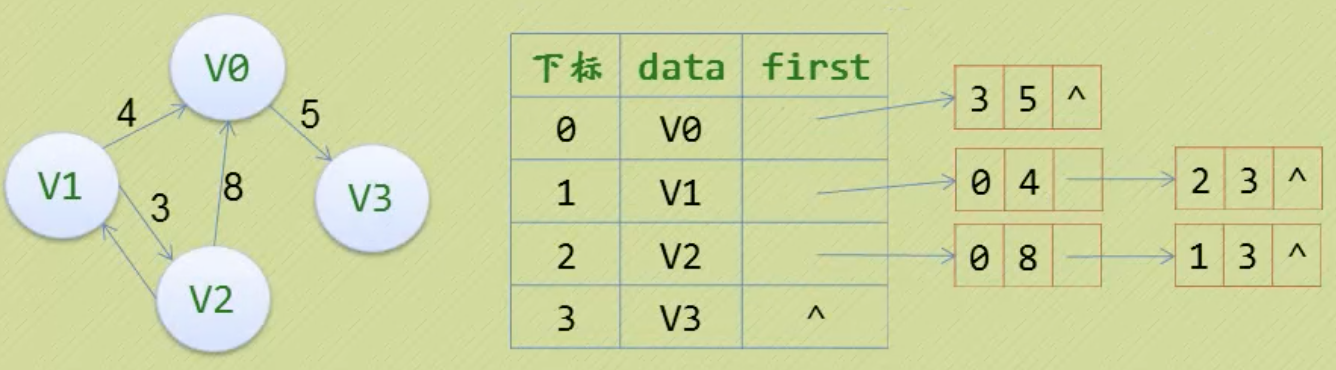
3. 十字链表
针对有向图的优化,结合邻接表和逆邻接表。定义顶点表结点结构包括数据、指向第一个入的邻接点的指针、指向第一个出的邻接点的指针:
![]()
边表结点结构:![]() ,tailVex弧尾顶点下标、headVex弧头顶点下标。也就是说一个结点中存的是两条弧。
,tailVex弧尾顶点下标、headVex弧头顶点下标。也就是说一个结点中存的是两条弧。

既容易找到以Vi为尾的弧,也容易找到以Vi为头的弧。
4.邻接多重表
无向图的应用中,如果关注的是边的操作而不是顶点,那么邻接表的操作就相对麻烦。仿照十字链表的做法对边表结构进行扩充:![]() ,iVex和 jVex是与某条边依附的两个顶点在顶点表中的下标,iLink指向依附顶点iVex的下一条边,jLink指向依附顶点jVex的下一条边。也就是说,边表存放的是一条边而不是一个顶点。
,iVex和 jVex是与某条边依附的两个顶点在顶点表中的下标,iLink指向依附顶点iVex的下一条边,jLink指向依附顶点jVex的下一条边。也就是说,边表存放的是一条边而不是一个顶点。

5.边集数组
两个一维数组,一个存储顶点信息,一个存储边的信息,边数组每个数据元素由一条边的起点下标、终点下标和权组成。

图的遍历
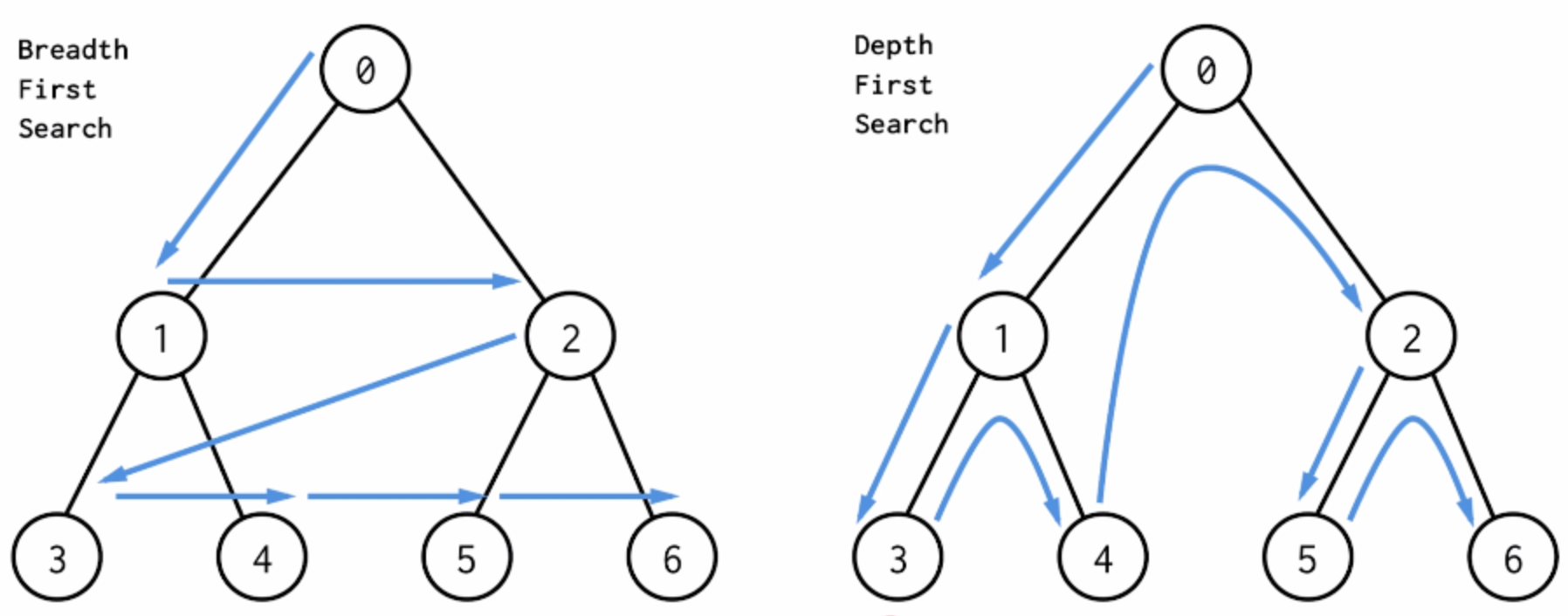
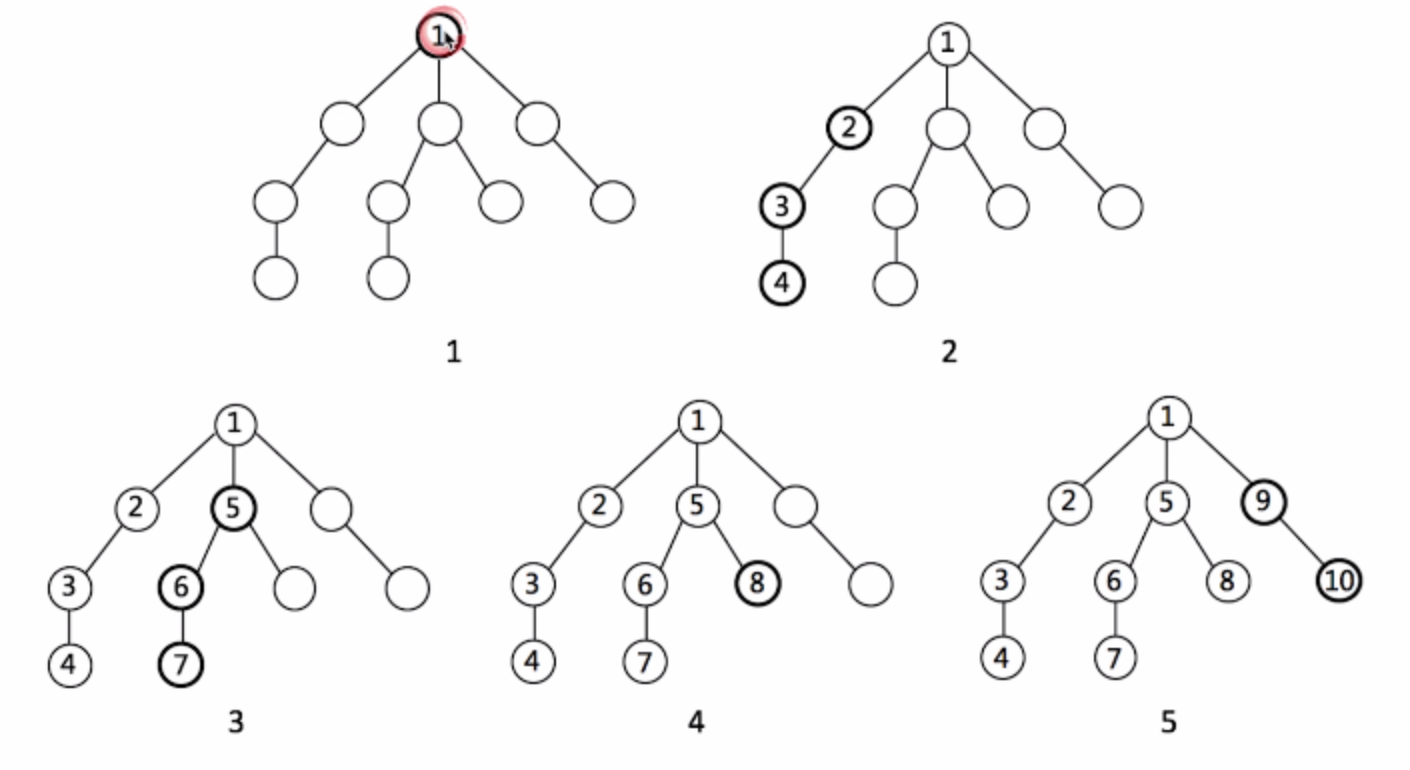
1. 深度优先遍历(dfs):更符合计算机的计算逻辑。
规定一个右手原则,没有碰到重复顶点的情况下一直向右,每过一个顶点就标记一次。重复顶点了就退回上一步,找没有重复的顶点。推到最开始的顶点了,遍历就结束。其实就是一个递归过程。
dfs 搜索方式,每次都一条路走到头,再回溯看看有没有其他的路可走。

1 visited = set() 2 3 def DFS(node, visited): 4 visited.add(node) 5 6 # process current node 7 ... 8 9 for next_node in node.children(): 10 if not next_node in visited: 11 DFS(next_node, visited)
非递归写法:

1 def DFS(tree): 2 if tree.root is None: 3 return [] 4 5 visited, stack = [], [tree.root] 6 7 while stack: 8 node = stack.pop() 9 visited.add(node) 10 11 process(node) 12 nodes = generate_related_nodes(node) 13 stack.push(nodes) 14 15 # other processing work 16 ...
马踏棋盘,遍历8*8的棋盘,其中马的走法规定为只有以下八个方向
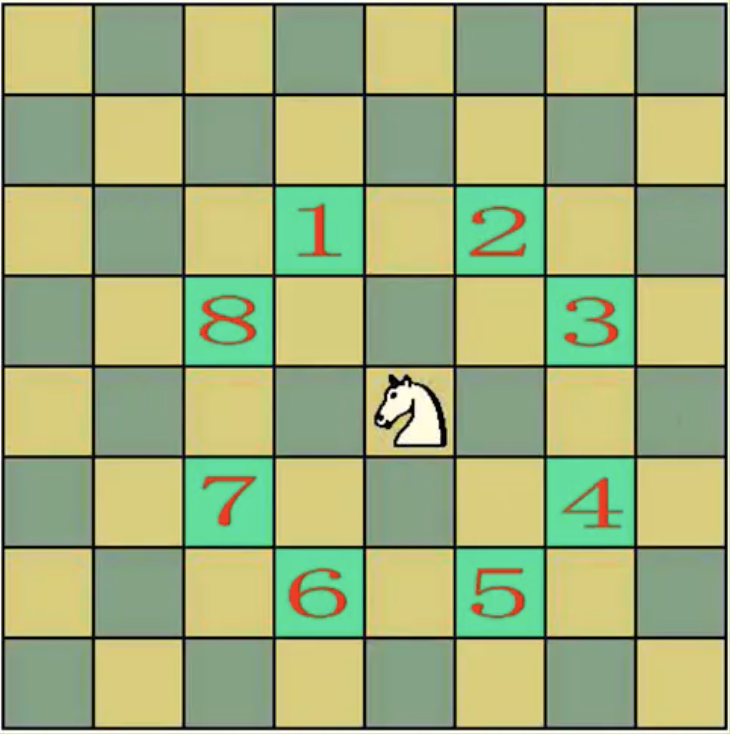
n >= 5且为偶数的情况下,以任意点作起始点都有解。
哈密尔顿路径:经过图中每个顶点且只经过一次的路径。

1 def ChessTraval(n=5, entry=(2,2)): 2 """棋盘大小n,出发点entry""" 3 4 def could_place(k): 5 # 检测边界和是否放过马 6 if (0<=res[k][0]<n) and (0<=res[k][1]<n) and (res[k] not in set(res[:k])): 7 return True 8 return False 9 10 def depthTraval(k): 11 if k == n**2: # 所有位置放完,得到一组解 12 output.append(res) 13 else: # 没放完的话就继续找res[k]的位置 14 for s in states: # 遍历point可能跳转的8个状态 15 res[k] = (res[k-1][0]+s[0], res[k-1][1]+s[1]) 16 if could_place(k): # 如果当前位置能放,去找后面所有可能的放法;不能放就跳过;回溯通过直接对res[k]赋值来实现 17 depthTraval(k+1) 18 19 states = [(-1, 2), (1, 2), (2, 1), (2, -1), (1, -2), (-1, -2), (-2, -1), (-2, 1)] 20 res = [None]*(n**2) # 一组解 21 output = [] # 所有解 22 res[0] = entry 23 depthTraval(1) 24 return output
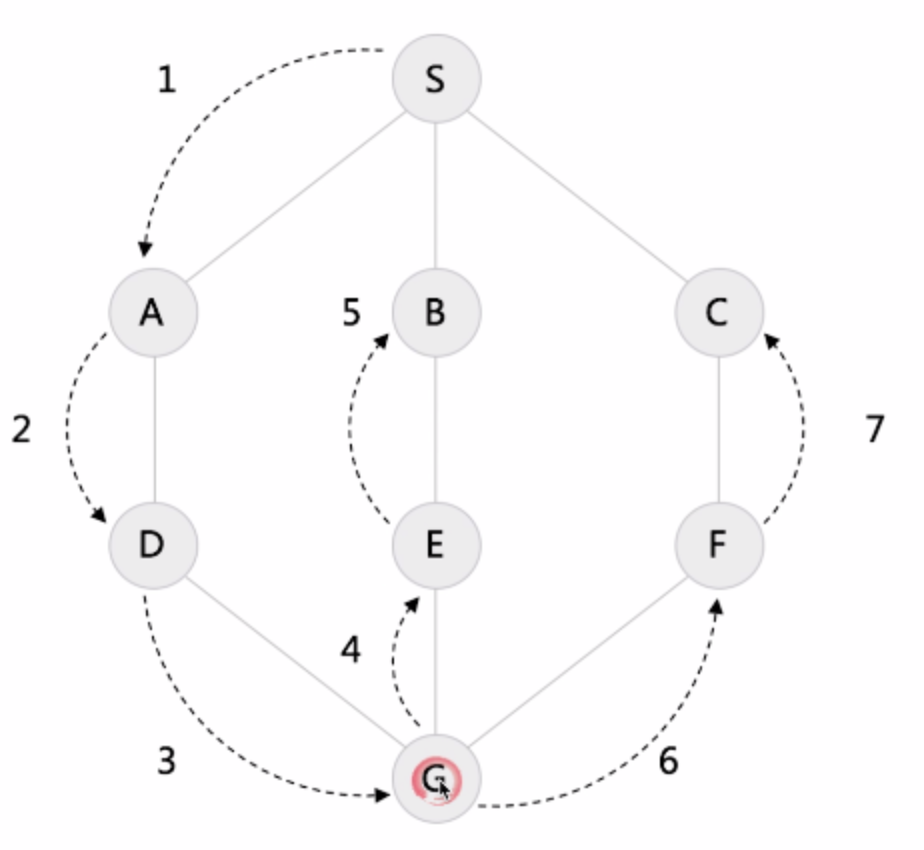
2. 广度优先遍历(bfs):直观且符合人类习惯,层层递进式的地毯式搜索。
用队列实现,从一个点A开始,A入队,A出队时按右手原则(从右到左)遍历所有和A相连的点(依次入队),再出队队中元素,每个元素出队时就将与其相连的点入队,已经遍历过的结点给一个标志之后即使再遇到也不入队。
bfs 搜索方式,以二叉树为例:
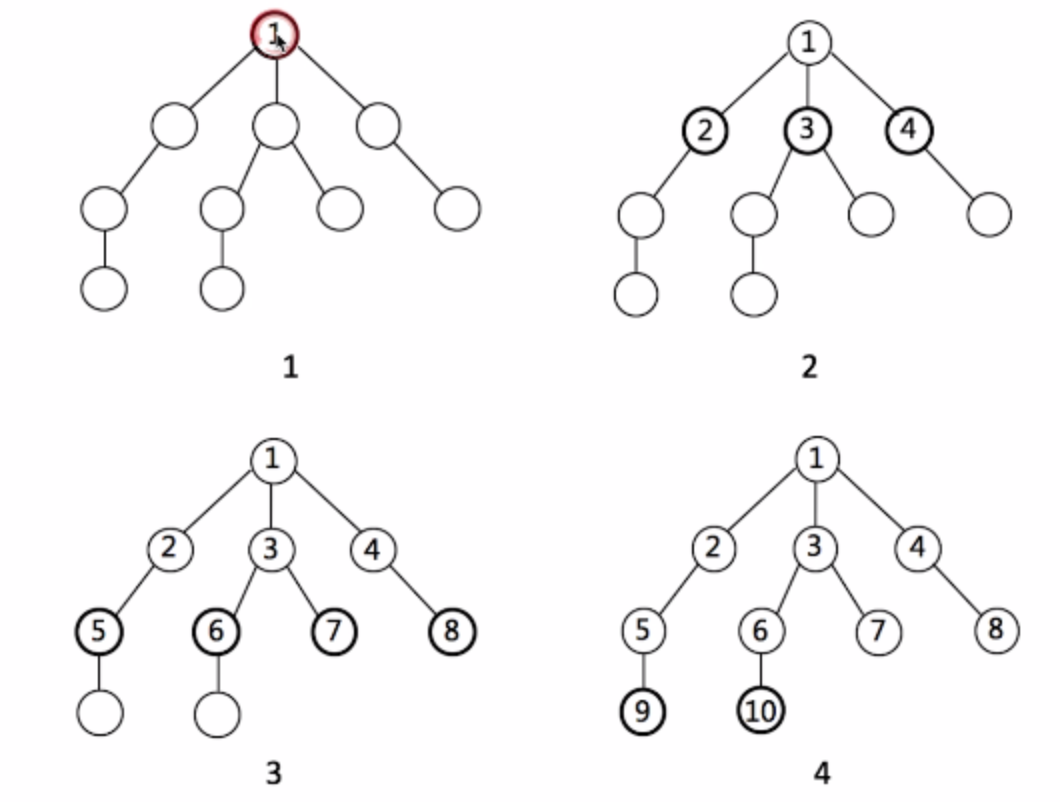

1 def BFS(graph, start, end): 2 queue = [] 3 queue.append([start]) # 队列 4 visited.add(start) # 集合 5 6 while queue: 7 node = queue.pop() 8 visited.add(node) 9 10 process(node) 11 nodes = generate_related_nodes(node) # 找node的后继节点,并判断是否被遍历过 12 queue.push(nodes) 13 14 # other processing work 15 ...
3. 剪枝

只保留最好的(非常确定)或数条比较好(不太确定当前最优分支是否是全局最优分支,优先搜索当前最优的分支)的分支进行后续搜索。
最小生成树
给定无向图,以最小成本的n-1条带权连线连接所有n个顶点。
1. prim算法:
1. 任意选出一个点作为初始顶点,标记为visit,计算所有与之相连接的点的距离,选择距离最短的点,标记visit。
2. 重复以下操作,直到所有点都被标记为visit:
在剩下的点中,计算与已标记的所有visit点距离最小的点(动态排序,取最小值),标记为visit,加入最小生成树。
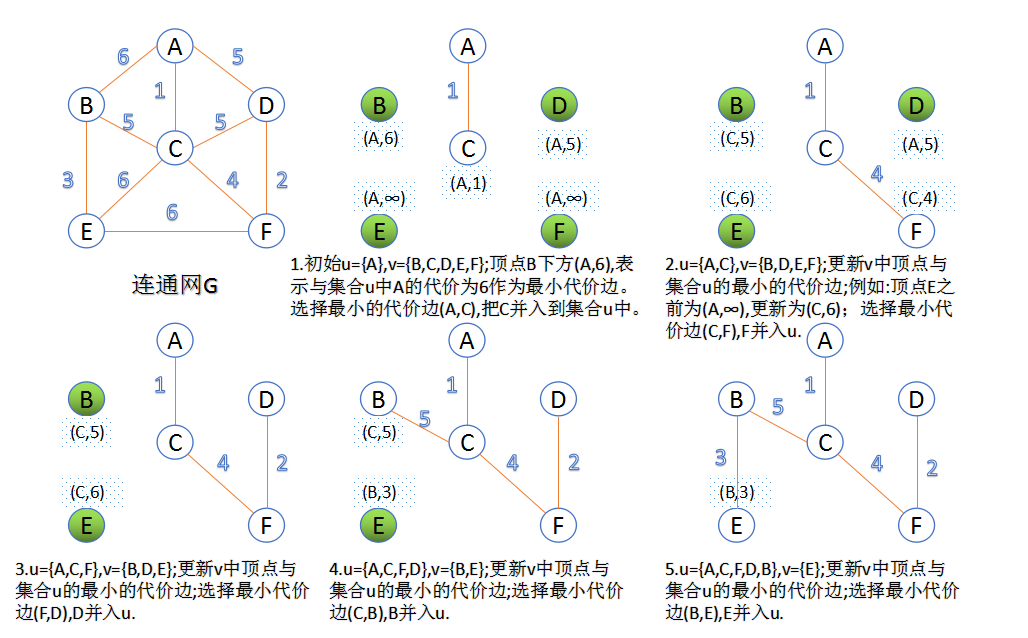

1 from collections import defaultdict 2 from heapq import * 3 4 def prim(vertices, edges): 5 """顶点vertices [v1, v2, ...] 6 带权无向边edges [(v1, v2, weight) ... ] 7 """ 8 adjecent_vertex = defaultdict(list) # defaultdict(list)必须以list做为变量 9 10 # 构建邻接矩阵,key是顶点,value是与key相连的点及边的权值 11 for v1, v2, length in edges: 12 adjecent_vertex[v1].append((length, v1, v2)) 13 adjecent_vertex[v2].append((length, v2, v1)) 14 # defaultdict(<type 'list'>, {'A': [(7, 'A', 'B'), (5, 'A', 'D')], 15 # 'C': [(8, 'C', 'B'), (5, 'C', 'E')], 16 # 'B': [(7, 'B', 'A'), (8, 'B', 'C'), (9, 'B', 'D'), (7, 'B', 'E')], 17 # 'E': [(7, 'E', 'B'), (5, 'E', 'C'), (15, 'E', 'D'), (8, 'E', 'F'), (9, 'E', 'G')], 18 # 'D': [(5, 'D', 'A'), (9, 'D', 'B'), (15, 'D', 'E'), (6, 'D', 'F')], 19 # 'G': [(9, 'G', 'E'), (11, 'G', 'F')], 20 # 'F': [(6, 'F', 'D'), (8, 'F', 'E'), (11, 'F', 'G')]}) 21 22 mst = [] # 存储最小生成树 23 chosed = set(vertices[0]) # 先选任意一个顶点作为起始,例如 A 24 adjecent_vertices_edges = adjecent_vertex[vertices[0]] # 与选中顶点相连的边的list [(7, 'A', 'B'), (5, 'A', 'D')] 25 heapify(adjecent_vertices_edges) # 加入堆中,之后能够用heapqpop动态取出最小值 26 27 while adjecent_vertices_edges: # 直到所有点都标记为visit为止 28 w, v1, v2 = heappop(adjecent_vertices_edges) # 取出与A相连的权最小边 (5, 'A', 'D') 29 if v2 not in chosed: # 如果D不在标记visit点中 30 chosed.add(v2) # 标记D 31 mst.append((v1, v2, w)) # 这条边加入最小生成树 32 for next_vertex in adjecent_vertex[v2]: # 再找所有与D相连的边,如果没有标记过就加入堆。因为与A相连的边已经加入过堆了 33 if next_vertex[2] not in chosed: 34 heappush(adjecent_vertices_edges, next_vertex) 35 return mst 36 37 # test 38 vertices = list("ABCDEFG") 39 edges = [ ("A", "B", 7), ("A", "D", 5), 40 ("B", "C", 8), ("B", "D", 9), 41 ("B", "E", 7), ("C", "E", 5), 42 ("D", "E", 15), ("D", "F", 6), 43 ("E", "F", 8), ("E", "G", 9), 44 ("F", "G", 11)] 45 print("edges:",edges) 46 print("prim:", prim(vertices, edges))
2. kruskal算法:
1. 将每个顶点放入自身的数据集合中,得到n个集合。
2. 按照权值的升序来选择边。每选择一条边,判断边的两个顶点是否在不同的集合中(并查集)。如果是,将此边加入最小生成树的集合中,同时将集合中包含这两个顶点的联合体取出;如果不是,就继续选择下一条边。
3. 重复2直到所有边都检查过。


1 X = dict() # 以全局变量X定义节点集合,即类似{'A':'A','B':'B','C':'C','D':'D'},如果A、B两点联通,则会更改为{'A':'B','B':'B",...},即任何两点联通之后,两点的值value将相同。 2 R = dict() # 各点的初始等级均为0,如果被做为连接的的末端,则增加1 3 4 5 # 节点的联通分量 6 def find(point): 7 if X[point] != point: 8 X[point] = find(X[point]) 9 return X[point] 10 11 # 连接两个分量(节点) 12 def merge(point1,point2): 13 r1 = find(point1) # v1的连通末端 14 r2 = find(point2) # v2的连通末端 15 if r1 != r2: # 如果连通末端不同,说明v1、v2不连通,不连通的情况下就令其连通 16 if R[r1] > R[r2]: # 如果v1的末端r1的连接等级高,连通后记为r2:r1 17 X[r2] = r1 18 else: # 如果r1没有更高,记为r1:r2 19 X[r1] = r2 20 if R[r1] == R[r2]: # 如果r1、r2连接等级相同,选择一个作为连接末端,连接等级加1 21 R[r2] += 1 22 23 def kruskal(vertices, edges): 24 # 设置 X、R 的初始值 25 for vertex in vertices: 26 X[vertex] = vertex 27 R[vertex] = 0 # 连接等级都为0 28 29 mst = set() 30 edges = list(edges) 31 edges.sort() # 按照权值升序来选择边 32 33 for edge in edges: # 直到所有边都检查过 34 w, v1, v2 = edge 35 if find(v1) != find(v2): # 判断边的顶点是否连通,如果不连通 36 merge(v1, v2) # merge顶点,将其连通 37 mst.add(edge) # 将此边加入最小生成树 38 return mst 39 40 # test 41 vertices = list('ABCDEF') 42 edges = set([ 43 (1, 'A', 'B'), 44 (5, 'A', 'C'), 45 (3, 'A', 'D'), 46 (4, 'B', 'C'), 47 (2, 'B', 'D'), 48 (1, 'C', 'D'), 49 ]) 50 result = kruskal(vertices, edges) 51 print('edges:', edges) 52 print('kruskal:', result)
最短路径
1. dijkstra算法:非负权有向图的单源最短路径问题。
1. 设置两个顶点的集合T和S,一个辅助向量D。S为已找到最短路径的顶点的集合,初始时,集合S中只有一个顶点,即源点v0;T是当前还未找到最短路径的顶点的集合;D的每个分量D[i] 表示当前找到的从源点v0到vi的最短路径长度(weight),初始时若v0到vi有弧则D[i]为弧上权值,否则为∞。
2. 在集合T中遍历找出当前长度最短的一条最短路径(v0,…,vk),从而将vk加入到顶点集合S中。然后检查新加入的顶点是否可以到达其他顶点,并且检查通过该顶点到达其他点的路径长度是否比从V0直接到达其他点更短。如果是,修改源点v0到T中各顶点的最短路径长度。
3. 重复2,直到所有的顶点都加入到集合S中。
长度为D[k] = Min{D[i] | vi in V}的路径就是从v0出发最短的一条路径 (v0, vi)。下一条长度次短的最短路径(v0到vj),要么直接是弧(v0, vj)、长度为弧上权值,要么是(v0, vk, vj)、长度为D[k] + (vk, vj)弧上权值。

1 from collections import defaultdict 2 from heapq import * 3 4 def dijkstra(edges, f, t): 5 """有向图的边,源点,目标点""" 6 g = defaultdict(list) # 构建邻接矩阵 7 for l,r,c in edges: 8 g[l].append((c,r)) 9 # {'A': [(7, 'B'), (5, 'D')], 10 # 'B': [(8, 'C'), (9, 'D'), (7, 'E')], 11 # 'C': [(5, 'E')], 12 # 'D': [(15, 'E'), (6, 'F')], 13 # 'E': [(8, 'F'), (9, 'G')], 14 # 'F': [(11, 'G')]}) 15 16 q = [(0, f, ())] # (源点到当前点的最短距离,当前点,对应的路径) 17 seen = set() # 集合s,已经找到最短路径的顶点的集合 18 mins = {} # 源点到T中各顶点最短路径长度,辅助向量D 19 while q: 20 cost, vk, path = heappop(q) # 源点到当前T中顶点的最短距离cost,对应顶点是vk 21 if vk not in seen: # 确保vk不在S中 22 seen.add(vk) # vk加入S中,也即退出T 23 path = (vk, path) # 记录源点到vk经过的路径 24 if vk == t: # 如果vk是目标点的话直接返回即可,就是最短距离和对应路径 25 return (cost, path) 26 27 # 如果vk不是目标点,检查vk是否可以到达其他顶点 28 for c, vj in g.get(vk, ()): # vk出度为0时返回() 29 if vj not in seen: # 只需要检查vk能到达的顶点中所有属于T的vj 30 prev = mins.get(vj, None) # D[j],源点到vj的最短路径,不存在时返回None 31 next_ = cost + c # D[vk] + (vk, vj)弧长 32 if prev is None or next_ < prev: # 如果路径v0-...-vk-vj权值比路径v0-vj更小 33 mins[vj] = next_ # 更新源点到T中最短距离 34 heappush(q, (next_, vj, path)) # 加入堆 35 36 return float("inf") 37 38 # test 39 edges = [ 40 ("A", "B", 7), 41 ("A", "D", 5), 42 ("B", "C", 8), 43 ("B", "D", 9), 44 ("B", "E", 7), 45 ("C", "E", 5), 46 ("D", "E", 15), 47 ("D", "F", 6), 48 ("E", "F", 8), 49 ("E", "G", 9), 50 ("F", "G", 11) 51 ] 52 53 print("=== Dijkstra ===") 54 print(edges) 55 print("A -> E:") 56 print(dijkstra(edges, "A", "E")) 57 print("F -> G:") 58 print(dijkstra(edges, "F", "G"))
2. floyd算法:解决有向图或负权(但不可存在负权回路)有向图任意两点间的最短路径。所有顶点到所有顶点到最短路径。
1. 引入两个矩阵,矩阵S中的元素s[i][j]表示顶点i(第i个顶点)到顶点j(第j个顶点)的距离。矩阵P中的元素p[i][j],表示顶点i到顶点j经过了p[i][j]记录的值所表示的顶点。
2. 假设图G中顶点个数为N,则需要对矩阵S和矩阵P进行N次更新。初始时,邻接矩阵S中s[i][j]表示为顶点i到顶点j的权值,如果i和j不相邻,则s[i][j]=∞;矩阵P的值为顶点p[i][j]的j的值。
3. 对矩阵D进行N次更新:
for k = 0, 1, ..., N-1,如果s[i][j] > s[i][k]+s[k][j],则更新s[i][k]为s[i][k]+s[k][j]”,且更新p[i][j]=p[i][k-1]

1 def Floyd(dis): 2 #min (Dis(i,j) , Dis(i,k) + Dis(k,j) ) 3 nums_vertex = len(dis[0]) 4 for k in range(nums_vertex): 5 for i in range(nums_vertex): 6 for j in range(nums_vertex): 7 if dis[i][j] > dis[i][k] + dis[k][j]: 8 dis[i][j] = dis[i][k] + dis[k][j] 9 return dis 10 11 # test 12 inf = float('inf') 13 matrix_distance = [[0,1,12,inf,inf,inf], 14 [inf,0,9,3,inf,inf], 15 [inf,inf,0,inf,5,inf], 16 [inf,inf,4,0,13,15], 17 [inf,inf,inf,inf,0,4], 18 [inf,inf,inf,inf,inf,0]] 19 20 print(Floyd(matrix_distance))
总结:图的DFS、BFS、Dijkstra、Floyd、Prim、Kruskal https://zhuanlan.zhihu.com/p/61628249
拓扑排序
无环有向图:DAG。小的工程或阶段称为“活动”。在一个表示工程的有向图无环图中,顶点表示活动,弧表示活动之间的优先关系,这样的有向图为顶点表示活动的网称为AOV网,表示活动之间存在某种制约关系。AOV网无回路。
拓扑序列:有向图顶点v1,...vn满足:vi到vj有一条路径,则顶点序列中vi必在vj之前。(只能前面的点指向后面的点)
拓扑排序:对一个有向图构造拓扑序列的过程。一个有向无环图可以有一个或多个拓扑排序序列。
对AOV网进行拓扑排序:
1. 选择一个没有前驱的顶点(入度为0)并且输出它。
2. 从网中删去该顶点,并且删去从该顶点出发的全部有向边。
3. 重复12直到网中不再存在没有前驱的顶点为止。

1 def topsort(Graph): 2 in_degrees = dict((u, 0) for u in Graph) 3 for u in G: 4 for v in G[u]: 5 in_degrees[v] += 1 # 每一个节点的入度 6 Q = [u for u in G if in_degrees[u] == 0] # 入度为0的顶点 7 S = [] # 拓扑序列 8 while Q: 9 u = Q.pop() # 默认从最后一个入度为0的顶点开始移除 10 S.append(u) # 加入到拓扑序列中 11 for v in G[u]: # 删去顶点u出发的有向边 12 in_degrees[v] -= 1 # 并移除其指向 13 if in_degrees[v] == 0: 14 Q.append(v) 15 return S 16 17 # test 18 Graph = {'a':'bf', 19 'b':'cdf', 20 'c':'d', 21 'd':'ef', 22 'e':'f', 23 'f':''} 24 print(topsort(Graph))
关键路径
AOE网:在一个表示工程的带权有向图中,顶点表示事件,有向边表示活动,边上权值表示活动持续时间。
源点:入度为0;汇点:出度为0。
关键路径:从源点到汇点距离最长的路径。一个工程可能会有多条关键路径。
缩短工程工期的核心就是缩短关键路径。
AOV和AOE的区别:
1. AOV用顶点表示活动的网,描述活动之间的制约关系。
2. AOE用边表示活动的网,边上的权值表示活动持续的时间。
3. AOE 是建立在子过程之间的制约关系没有矛盾的基础之上,再来分析整个过程需要的时间。
事件最早开始时间etv:顶点Vi最早发生的时间。(从前往后推,v0到vi的最长路径长度)
事件最晚开始时间ltv:顶点Vi最晚发生的时间,超出则会延误整个工期。(从后往前推,不影响工期的最晚开工时间)
活动的最早开始时间ete:边Eg最早发生时间。(若以vi为弧尾,则ete就等于vi的etv)
活动的最晚开始时间lte:边Eg最晚发生时间。不推迟工期的最晚开工时间。
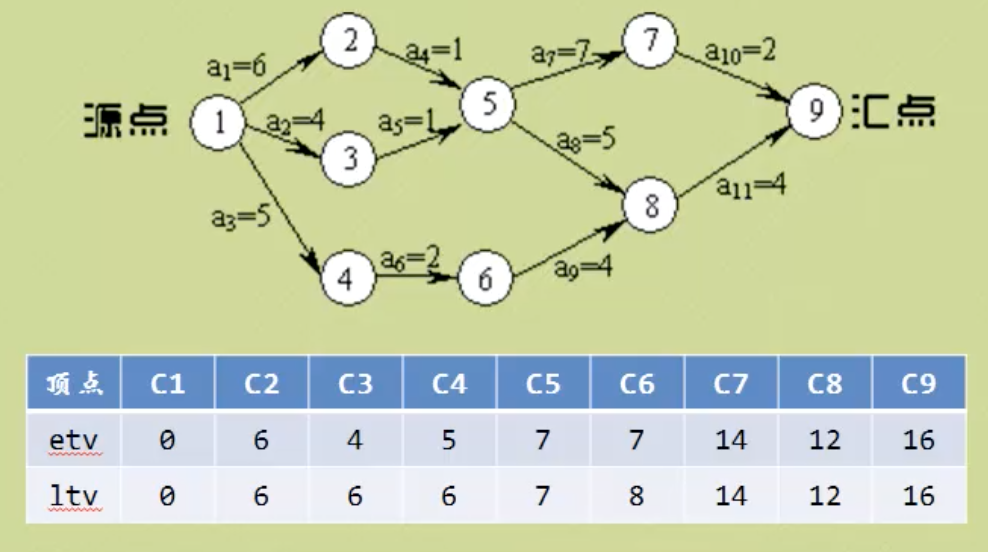

只需要确认每个顶点的最早开始时间和最晚开始时间,判断它们的时间差,如果没有时间差就是关键路径。
1. 输入顶点数和边数,已经各个弧的信息建立图
2. 从源点v1出发,按照拓扑序列往前求各个顶点的最早发生时间。如果得到的拓扑序列个数小于网的顶点数n,说明建立的图有环,无关键路径,直接结束。
3. 从终点vn出发,按逆拓扑序列,往后求其他顶点最晚发生时间。
4. 若etv等于ltv,说明是关键活动。

1 def topsort(graph): 2 vnum = len(graph) # 顶点数 3 indegree = dict((u, 0) for u in range(vnum)) 4 topseq = [] 5 6 for x in range(vnum): 7 for y in range(vnum): 8 if graph[x][y] > 0: 9 indegree[y] += 1 # 入度表 10 11 Q = [y for y in range(vnum) if indegree[y] == 0] 12 13 while Q: 14 u = Q.pop() 15 topseq.append(u) 16 for y in range(vnum): 17 if graph[u][y] > 0: 18 indegree[y] -= 1 19 if indegree[y] == 0: 20 Q.append(y) 21 return topseq 22 23 def critcal_path(graph): 24 def events_earliest_time(graph, topseq): # 计算事件最早发生事件 25 vnum = len(graph) 26 ee = [0]*vnum # v0到vi的最大路径长度 27 for i in topseq: 28 for j in range(vnum): 29 if graph[i][j] != 0: 30 if ee[i] + graph[i][j] > ee[j]: # ee[i]表示v0到vi的最长路径 31 ee[j] = ee[i] + graph[i][j] # 如果v0-...-vi-vj的路径长度大于v0-...-vj,更新ee[j] 32 return ee 33 34 35 def events_latest_time(graph, topseq, eelast): # 计算时间最晚发生时间 36 vnum = len(graph) 37 le = [eelast]*vnum # 各顶点的最晚发生时间,初始化为汇点的最早发生时间 38 for k in range(vnum-2, -1, -1): 39 i = topseq[k] 40 for j in range(vnum): 41 if graph[i][j] != 0: 42 if le[i] + graph[i][j] > le[j]: # 如果vi最晚时间+ij工期超过了vj最晚时间,说明耽误了工期,更新vi最晚时间 43 le[i] = le[j] - graph[i][j] 44 return le 45 46 def crt_road(graph, ee, le): 47 crt = [] 48 # 可能不只一条关键路径,只遍历ee等于le的顶点不能完全确定路径 49 for i in range(vnum): 50 for j in range(vnum): 51 if graph[i][j] > 0: 52 if ee[i] == le[j]-graph[i][j]: # ee[i] == le[i] 53 crt.append((i, j, ee[i])) 54 return crt 55 56 vnum = len(graph) 57 topseq = topsort(graph) 58 if (not topseq) or len(topseq)<vnum: 59 return None 60 ee = events_earliest_time(graph, topseq) 61 le = events_latest_time(graph, topseq, ee[-1]) 62 return crt_road(graph, ee, le) 63 64 # test 65 graph = [[0,7,13,8,0,0,0,0,0], 66 [0,0,4,0,0,14,0,0,0], 67 [0,0,0,0,5,0,8,12,0], 68 [0,0,0,0,13,0,0,10,0], 69 [0,0,0,0,0,7,3,0,0], 70 [0,0,0,0,0,0,0,0,5], 71 [0,0,0,0,0,0,0,0,7], 72 [0,0,0,0,0,0,0,0,8], 73 [0,0,0,0,0,0,0,0,0]] 74 print(topsort(graph)) 75 print(critcal_path(graph))
