容斥原理与莫比乌斯反演的关系

//容斥原理，c[i]表示i当前要算的次数，复杂度和第二层循环相关 O(nlogn~n^2)
LL in_exclusion(int n,int *c)
{
    for(int i=0;i<=n;i++) c[i]=1;    //不一定是这样初始化，要算到的才初始化为1
    LL ans=0;
    for(int i=0;i<=n;i++) if(i要算)
    {
        ans+=(统计数)*c[i];
        for(int j=i+1;j<=n;j++) if(i会算到j) c[j]-=c[i];//j要算的次数减去算i时已经算了的次数
    }
    return ans;
}

容斥原理伪代码

容斥原理结论：

1~n中x的倍数有n/x个,因而gcd(a1,a2,...,am)=kx(1<=ai<=n)中的ai都在这n/x个数中，若ai<a(i+1),则可用容斥原理算出gcd(a1,a2,...,am)=x的对数。

也可以用莫比乌斯反演：

当F(n) = sigma{f(d),n|d}，则f(n) = sigma{mu(d/n)*F(d),n|d}

f(x)表示1~n中选m个数gcd=x的个数，则F(x)表示1~n中选m个数的gcd=kx的个数

然后f(n)=sigma{mu(x/n)*F(x),n|x}

题目链接：https://icpc.njust.edu.cn/Problem/Local/1923/

这里容斥原理算出的c[i]和莫比乌斯函数u[i]相等，说明莫比乌斯反演就是一种容斥，

不过是逆思维的容斥,即将问题细分为互斥的最小元，所有最小元的并就是结果

因此，别的容斥也可以将算的过程中需要用到的u[i]一次算出，后面直接利用该数组

如F(n)=sigma{f(x),x和n满足的条件}<==>f(n)=sigma{u(逆条件)*F(x),x和n满足的条件}

这个结论在国家集训队2013论文集中的浅谈容斥原理有提到

 1 LL in_exclusion(int x,int n,int *c)
 2 {
 3     n/=x;
 4     for(int i=0;i<=n;i++) c[i]=1;
 5     LL ans=0;
 6     for(int i=2;i<=n;i++)
 7     {
 8         ans+=C(n/i,m)*c[i];
 9         for(int j=i<<1;j<=n;j+=i) c[j]-=c[i];
10     }
11     return C(n/i,m)-ans;
12 }

View Code

莫比乌斯反演：

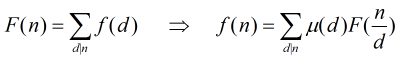
当F(n) = sigma{f(d),d|n}，则f(n) = sigma{mu(d)*F(x/d),d|n}

当F(n) = sigma{f(d),n|d}，则f(n) = sigma{mu(d/n)*F(d),n|d}

b是a的倍数记作a|b

莫比乌斯函数μ(d)定义

若d=1 那么μ(d)=1

若d=p1p2…pr （r个不同质数，且次数都为一）μ(d)=(-1)^r

其余 μ(d)=0

 1 void getMu(int *mu) 
 2 {
 3     for (int i = 1; i <N; ++i) 
 4     {
 5         int target = i == 1 ? 1 : 0;
 6         int delta = target - mu[i];
 7         mu[i] = delta;    
 8         for (int j = 2 * i; j <N; j += i) mu[j] += delta;
 9     }
10 }

//计算N的Mobius函数u(N) (mu数组) O(nlogn)

 1 void getMu(bool *vis,int *p,int *mu,int &pn)  //O(n)
 2 {  
 3     memset(vis,0,sizeof(vis));  
 4     mu[1]=1;  
 5     pn=0;  
 6     for(int i=2; i<N; i++)  
 7     {  
 8         if(!vis[i]) { p[pn++]=i;mu[i]=-1; }  
 9         for(int j=0; j<pn&&i*p[j]<N; j++)  
10         {  
11             vis[i*p[j]]=1;  
12             if(i%p[j]) mu[i*p[j]]=-mu[i];  
13             else { mu[i*p[j]]=0;break;}  
14         }  
15     }  
16 }

//计算N的Mobius函数u(N) (mu数组) O(n)

莫比乌斯反演求lcm(i,j),1<=i<=n,1<=j<=m的和:

设f(d)=lcm(x,y)/(d^2) (gcd(x,y)==d),

则F(x)=(1+n)*n/2 * (1+m)*m/2,

所以F(x)=sigma{d/x*f(d),x|d},

所以f(x)=sigma{d/x * u(d/x) * F(d),x|d},

所以ans=sigma{f(d)*d,1<=d<=min(n,m)},

ans=sigma{sigma{F(d) * d/x * u(d/x),x|d}*x,1<=d<=min(n,m)}

ans=sigma{sigma{d/x *u(d/x),x|d} *d *F(d),1<=d<=min(n,m)}

设sum[d]=sigma{d/x *u(d/x),x|d},在线性筛时

如果d%p[i]==0,sum[d*p[i]]=sum[d];

如果d%p[i]!=0,sum[d*p[i]]=-sum[d]*p[i]+sum[d];

然后求sum[d]*d的前缀和分块优化即可

1                 for(int i=1;i<=n;)//利用c[i]前缀和sqrt(n)优化
2         {
3             int x=n/i;
4             int y=n/x;
5             ans+=(c[y]-c[i-1]) * count(x);
6             i=y+1;
7         }

//利用c[i]前缀和sqrt(n)优化

 1 LL in_exclusion(int n,int *c)
 2 {
 3     for(int i=0;i<=n;i++) c[i]=1;    //不一定是这样初始化，要算到的才初始化为1
 4     LL ans=0;
 5     for(int i=0;i<=n;i++) if(i要算)
 6     {
 7         ans+=(统计数)*c[i];
 8         for(int j=i+1;j<=n;j++) if(i会算到j) c[j]-=c[i];//j要算的次数减去算i时已经算了的次数
 9     }
10     return ans;
11 }

//容斥原理，c[i]表示i当前要算的次数，复杂度和第二层循环相关 O(nlogn~n^2)

Gcd(a,b)=k ==> gcd(a/k,b/k)=1，然后反演或容斥，必要时要sqrt分块优化

分块加速：d在[i,n/(n/i)]中n/d相等

然后我们注意到[n/i]*[m/i]在一定的范围内是不变的，这个范围是[i,min(n/(n/i),m/(m/i)]，这样我们可以预处理出c[i]的前缀和，然后加快运算（复杂度网上说是O(sqrt(n))的，实测具体数值接近2*sqrt(n)）

 1 LL slove(int *c)
 2 {
 3     LL ans=0;
 4     if(m<n) swap(m,n);        //m>=n
 5     for(int i=1,last=i;i<=n;i=last+1)
 6     {  
 7         last=min(n/(n/i),m/(m/i));  
 8         ans+=(LL)(c[last]-c[i-1])*(n/i)*(m/i);  
 9     } 
10     return ans;
11 }

//c数组u函数前缀和，则sigma{gcd(n,m)=i,i<=min(n,m)}可由以下方法在sqrt(n)的复杂度内求出

若a,b范围不同，即a<=n,b<=m,容斥算gcd(a,b)=1的时候变成a*b即可

莫比乌斯反演总结：

　　莫比乌斯反演一般用于解决与质数有关的计数问题，正常情况下莫比乌斯反演的题目都能用容斥原理解决，但莫比乌斯反演可以通过O(n)的筛法筛出mu函数，并且可以通过分块加速将每个查询所花的时间降到sqrt(n)，当题目所给时间不多时就必须用莫比乌斯反演了

　　当O(sqrt(n))查询也T了的时候考虑用欧拉函数优化来做到O(n)预处理，O(1)查询