一 概念
卡特兰数又称卡塔兰数,是组合数学中一个常出现在各种计数问题中出现的数列。
卡特兰数前几项为 : 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900,
2674440, 9694845, 35357670, 129644790,
令h(0)=1,h(1)=1,catalan数满足递推式[1]:
h(n)= h(0)*h(n-1)+h(1)*h(n-2) + ... + h(n-1)h(0) (n>=2)另类递推式[2]:h(n)=h(n-1)*(4*n-2)/(n+1);
递推关系的解为:h(n)=C(2n,n)/(n+1) (n=0,1,2,...) 递推关系的另类解为:h(n)=c(2n,n)-c(2n,n+1)(n=0,1,2,...)二 建模方法
模型为
0
简单的测试: 找到 一个模型的前几项等于卡特兰数1,1,2,5,14
1 (这个是充分条件)卡特兰数的应用可归结为一句话:n个a和n个b组成一个排列,保证它的前缀中a的个数大于b的个数 或者
2 (这个是充要条件)归结为这个组合排列问题可以进行分段,用卡特兰数表示h(n)=∑h(i-1)h(n-i)
注意:第一个元素一般是固定的;进行分段时,使用第一个元素对整个序列进行划分。或者
3 (这个是充要条件)转换为h(n)=c(2n,n)-c(2n,n+1)(n=0,1,2,...)
4 等价于在方格中计算路径数
三常见应用
实质上都是递推等式的应用
括号化
矩阵链乘: P=a1×a2×a3×……×an,依据乘法结合律,不改变其顺序,只用括号表示成对的乘积,试问有几种括号化的方案?(h(n)种) 建模:2n个括号即n对括号,第一个左括号是不变的,那么与之相匹配的括号在位置2i。则把整体的分成两段:在第一队括号内的有i-1对括号,在在第一个括号外的有n-i对括号。则h(n)=∑h(i-1)h(n-i),i从1到n
出栈次序
一个栈(无穷大)的进栈序列为1,2,3,…,n,有多少个不同的出栈序列?建模:此处百度百科里面说的较为含糊。
假设第一个元素的出栈序号为i,那么出栈分成两段:前i-1个数和后n-i个数
第一个元素出栈,说明栈为空;第一个元素的出栈序号为i,说明有在此之前i-1个元素出栈,在此之后有n-i个元素出栈。
凸多边形三角划分
在一个凸多边形中,通过若干条互不相交的对角线,把这个多边形划分成了若干个三角形。现在的任务是键盘上输入凸多边形的边数n,求不同划分的方案数f(n)。比如当n=6时,f(6)=14。类似问题
一位大城市的律师在她住所以北n个街区和以东n个街区处工作。每天她走2n个街区去上班。如果她从不穿越(但可以碰到)从家到办公室的对角线,那么有多少条可能的道路? 在圆上选择2n个点,将这些点成对连接起来使得所得到的n条线段不相交的方法数?
给定节点组成二叉树
给定N个节点,能构成多少种不同的二叉树?[7] (能构成h(N)个) (这个公式的下标是从h(0)=1开始的)
四 扩展:图形化建模
1 就是给定n个元素,依次通过一个栈,求可能的出栈序列的个数。

下面我们来看一种图形化的方法证明这个等式,很容易理解的。
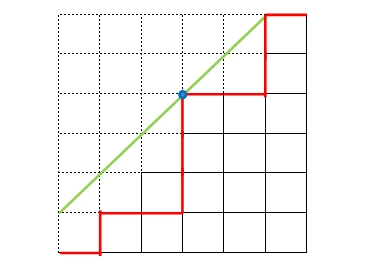
我们把对n个元素的n次进栈和n次出栈理解为在一个n * n的方格中向右走n次(代表进栈),向上走n次(代表出栈)。由于出栈次数不能大于进栈次数,我们可以得到这样一个方格:

每次沿着实线走,所以,只要求出从方格左下角到右上角路径的个数即可。
我们把表格补全,考虑每一条不合法的路径,如
在这条路径上,必然有一个地方连续两次向上,即从图上蓝点处开始,而且这个点必然在如图所示的绿线上。我们以这个点为起点,把到左上角整条路经取反,也就是对称上去,得到一条新路径,但是超出了表格。我们知道,这条路径包括n + 1次向上和n – 1次向下,也就是在一个(n + 1) * (n - 1)的方格中。由此我们知道,一条不合法路径必然对应一个(n + 1) * (n - 1)方格中的路径。同样地,对于(n + 1) * (n - 1)方格中任意一条路径,以这条路径与绿线的第一个交点为起点到方格的右上方全部取反,即可得到一个在n * n方格中的不合法路径。
我们通过这样的方法确定了每条不合法路径与一个(n + 1) * (n - 1)方格中路径的一一对应关系,因此,方格中不合法路径总数为C(2n, n - 1),而所有路径总数为C(2n, n),两式相减即为原组合等式。
2 2进制数
对于在n位的2进制中,有m个0,其余为1的catalan数为:C(n,m)-C(n,m-1)。证明可以参考标准catalan数的证明。[8] 问题1的描述:有n个1和m个-1(n>=m),共n+m个数排成一列,满足对所有0<=k<=n+m的前k个数的部分和Sk > 0的排列数。 问题等价为在一个格点阵列中,从(0,0)点走到(n,m)点且不经过对角线x==y的方法数(x > y)。 考虑情况I:第一步走到(0,1),这样从(0,1)走到(n,m)无论如何也要经过x==y的点,这样的方法数为(( n+m-1,m-1 )); 考虑情况II:第一步走到(1,0),又有两种可能: a . 不经过x==y的点;(所要求的情况) b . 经过x==y的点,我们构造情况II.b和情况I的一一映射,说明II.b和I的方法数是一样的。设第一次经过x==y的点是(x1,y1),将(0,0)到(x1,y1)的路径沿对角线翻折,于是唯一对应情况I的一种路径;对于情况I的一条路径,假设其与对角线的第一个焦点是(x2,y2),将(0,0)和(x2,y2)之间的路径沿对角线翻折,唯一对应情况II.b的一条路径。 问题的解就是总的路径数 ((n+m, m)) - 情况I的路径数 - 情况II.b的路径数。 ((n+m , m)) - 2*((n+m-1, m-1)) 或: ((n+m-1 , m)) - ((n+m-1 , m-1)) 问题2的描述:有n个1和m个-1(n>=m),共n+m个数排成一列,满足对所有0<=k<=n+m的前k个数的部分和Sk >= 0的排列数。(和问题1不同之处在于此处部分和可以为0,这也是更常见的情况) 问题等价为在一个格点阵列中,从(0,0)点走到(n,m)点且不穿过对角线x==y的方法数(可以走到x==y的点)。 把(n,m)点变换到(n+1,m)点,问题变成了问题1。 方法数为: ((n+m+1, m)) - 2*((n+m+1-1, m-1)) 或: ((n+m+1-1, m)) - ((n+m+1-1, m-1))
大部分参考自:http://baike.baidu.com/view/2499752.htm
http://blog.163.com/wangenze_black@126/blog/static/110710515200962110481040/