极大似然估计法是求点估计的一种方法，最早由高斯提出，后来费歇尔（Fisher）在1912年重新提出。它属于数理统计的范畴。
大学期间我们都学过概率论和数理统计这门课程。
概率论和数理统计是互逆的过程。概率论可以看成是由因推果，数理统计则是由果溯因。
用两个简单的例子来说明它们之间的区别。
由因推果（概率论）
例1：设有一枚骰子，2面标记的是“正”，4面标记的是“反”。共投掷10次，问：5次“正”面朝上的概率？
解：记 “正面”朝上为事件A，正面朝上的次数为x。
由题意可知 :
更一般的有：
例2: 设有一枚骰子，其中“正面”所占的比例为ω ω
。共投掷n n
次，问：k k
次“正”面朝上的概率？
解：记 “正面”朝上为事件A，正面朝上的次数为x。
有题意可知: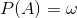
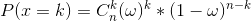
例3：设有一枚骰子，做了n n 次实验，其中k k 次“正面”朝上。问：这枚骰子中，“正面”所占的比例ω ω 是多少？
在例2中，因为我们对骰子模型了解的很透彻，即知道这类实验中ω ω 的具体数值。因此可以预测某一事件发生的概率。
在例3中，我们并不能完全了解模型精确参数。我们需要通过实验结果来估计模型参数。也就是由果溯因(数理统计)。
总结来看如下：
| 例2 | 已知 ω | 求事件发生的 k 次的概率 |
|---|---|---|
| 例3 | 已知事件发生了 k 次 | 估计 ω |
| Giving ω | Calculate the probability distribution of random variable | |
|---|---|---|
| LF | Giving random variable | Calculate the the probability distribution of ω |
由于事件发生的概率越大，就越容易发生。所以例3可理解为：ω是多大时，k次“正面”朝上发生的概率最大？
计算的时候，对表达式求最大值，得到参数值估计值。
这就是极大似然估计方法的原理：用使概率达到最大的那个ω ^ ω^
来估计未知参数ω。
这也把一个参数估计问题转化为一个最优化问题。
此外，我们甚至不知道一个系统的模型是什么。因此在参数估计前，先按照一定的原则选择系统模型，再估计模型中的参数。本文为了简单，模型设定为伯努利模型。
以上是对极大似然估计方法理论上的介绍，接下来介绍计算方法。
计算方法
为了表述规范，引入
概率密度函数：
通过调换“实验结果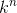
”与“模型参数
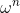”的位置有 似然函数：
通过例4 介绍概率密度函数与似然函数之间的区别：
例4.1 设有一枚骰子，1面标记的是“正”，4面标记的是“反”。共投掷10次，设“正面”的次数为k，求k的概率密度函数。
解：
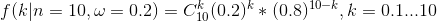
从图中可以看出，“正面”次数为2的概率最大。它是关于k的函数。
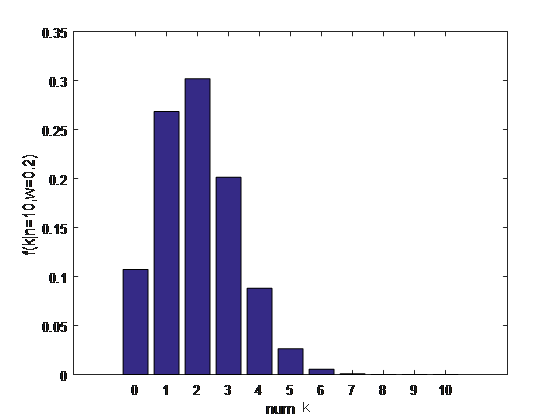
例4.2 设有一枚骰子。共投掷10次，“正面”的次数为2，求“正面”所占的比例，即ω的值。
似然函数：
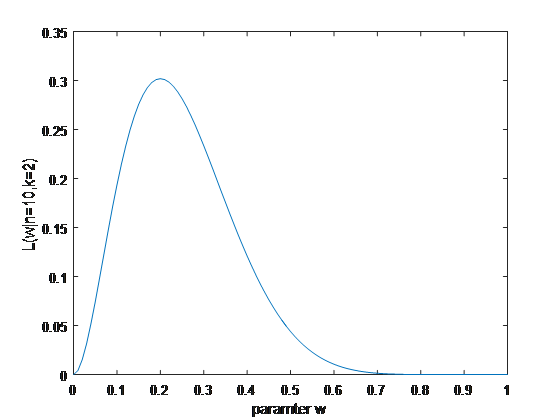
因此概率密度函数是指 在参数已知的情况下，随机变量的概率分布情况。
似然函数是指 在随机变量已知的情况下，参数取值的概率分布情况。
例5：设有一枚骰子，做了10次实验，其中3次“正面”朝上。问：这枚骰子中，“正面”所占的比例是多少？
解：
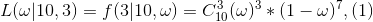
我们根据极大似然估计方法的原理：用使概率达到最大的那个ω ̂来估计未知参数ω
对于简单的连续函数，求最大值的方法为：函数表达式一阶导数等于0，二阶导数小于0。
为了计算简单，对上式两边取对数：
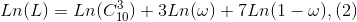
一阶条件：
将（2）式对ω求偏导数（导数）：
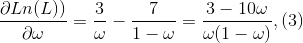
令（3）式为0，解得ω=0.3
二阶条件：
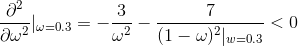
因此 ω=0.3时，（1）式取得最大值。根据极大似然估计理论，“正面”所占的比例为0.3
例6：设有一枚神奇的骰子，“正面”所占的比例为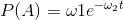
。t代表实验时间点。
已知：在t i =1,3,6,9,12,18共6个时刻做实验，每个时刻做n=100次实验。“正面”朝上的次数分别为：x i =94,77,40,26,24,16
求：参数ω=(ω 1 ，ω 2 )>0 的估计值，。
解：
求出“正面”朝上的概率密度函数：
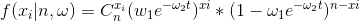
似然函数：
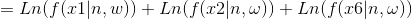
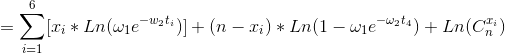
对于这样一个复杂的非线性约束优化问题，利用求导的方式不再可行。可借助matlab进行计算。
###代码如下： function f = objfun( x )
f = -(94*log(x(1)*exp(-x(2)*1))+6*log(1-(x(1)*exp(-x(2)*1))) + ...
77*log(x(1)*exp(-x(2)*3))+23*log(1-(x(1)*exp(-x(2)*3))) + ...
40*log(x(1)*exp(-x(2)*6))+60*log(1-(x(1)*exp(-x(2)*6))) + ...
26*log(x(1)*exp(-x(2)*9))+74*log(1-(x(1)*exp(-x(2)*9))) + ...
24*log(x(1)*exp(-x(2)*12))+76*log(1-(x(1)*exp(-x(2)*12))) + ...
16*log(x(1)*exp(-x(2)*18))+84*log(1-(x(1)*exp(-x(2)*18))));
end
sample5.m
x0 = [0.1,0.1]; %给定初值
lb = [0,0]; %给定下限
ub = []; %给定上限
[x,fval] = fmincon(@objfun,x0,[],[],[],[],lb,ub)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
解得：
x =
1.070111883136768 0.130825782195123
fval =
3.053055671586732e+02
本笔记参考https://blog.csdn.net/chenjianbo88/article/details/52398181
https://blog.csdn.net/saltriver/article/details/63681339
及李航的《统计学方法》第一章