【2017-03-23 这篇弃掉了,请看新笔记 】
参考资料:
[大部分还没看完,目前主要看了popoqqq那篇 orz]
http://wenku.baidu.com/link?url=Kzzxkk64CFU7sfDeJbGKNpZpFJzJY1ZwNoaPgGo7tPSpv4KJvGAkStkpzytG46gjQuqNX7NB0merxfS4knD2H5fw7s4oHu1o1-6p16_VbEm
http://wenku.baidu.com/view/77396ebb27d3240c8547ef2e.html?re=view
http://vfleaking.blog.uoj.ac/slide/87
【零】
什么是反演:
假设有两个函数 f 和 g 满足:
f(n)=∑k a[n,k]*g(k)
已知 f 求 g 的过程就称为反演。
【一】
- 若f(n)的定义域为正整数域,值域为复数,即f:Z+→C,则称f(n)为数论函数。
- 若f(n)为数论函数,且f(1)=1,对于互质的正整数p,q有f(p⋅q)=f(p)⋅f(q),则称其为积性函数。
- 若f(n)为积性函数,且对于任意正整数p,q都有f(p⋅q)=f(p)⋅f(q),则称其为完全积性函数。
- 积性函数的前缀和也是积性函数
【二】
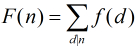 ---->
---->
形式二:

【莫比乌斯函数】
1.
- 莫比乌斯函数μ(n),在狄利克雷卷积的乘法中与恒等函数互为逆元,mu*1=e
- 积性函数. 证明:μ(n)=∏μ(pi^ei),每个pi^ei是互质的
- μ(1)=1
- μ(n)=(-1)^k 若n是k个不同prime之积 (质因子的次数都为1)
- 0 其他情况
2.性质:
(1)
证明:n!=1时,质因子次数都为1,i个质因子的有C(k,i)个,
列出来根据二项式定理
得证
就是容斥原理,奇数个质因子减,偶数个质因子加,
(2)
n=Σ{d|n | phi(d)}
证明:
i/n化为最简分数j/d,那么d|n且gcd(j,d)=1
以d为分母的最简分数有phi(d)个
一共n个分数
(3)
证明:用上面那个式子,裸上莫比乌斯反演 f(n)=n,g(n)=phi(n)
3.求莫比乌斯函数
线性筛
bool notp[N];
int p[N],mu[N];
void sieve(){
mu[1]=1;
for(int i=2;i<=N-1;i++){
if(!notp[i]) p[++p[0]]=i,mu[i]=-1;
for(int j=1;j<=p[0]&&i*p[j]<=N-1;j++){
int t=i*p[j];
notp[t]=1;
if(i%p[j]==0){
mu[t]=0;
break;
}
mu[t]=-mu[i];
}
}
}
【莫比乌斯反演的证明】
【一句话】
莫比乌斯反演就是偏序集上的容斥原理
用处:
来自popoqqq:
- 对于一些函数f(n),如果我们很难直接求出它的值,而容易求出倍数和或约数和F(n),那么我们可以通过莫比乌斯反演来求得f(n)的值
- 例:f(n)表示某一范围内(x,y)=n的数对的数量,F(n)表示某一范围内n|(x,y)的数对的数量
- 那么直接求f(n)并不是很好求,而F(n)求起来相对无脑一些,我们可以通过对F(n)进行莫比乌斯反演来求得f(n)


