说出来可能不信,这已经是我第三次入门DFS和BFS了,大佬都救不了我的那种,所以我打算自救,这里我会慢慢整理对于DFS和BFS自己的理解,我不想再拿到DFS和BFS的题目之后只能和他大眼瞪小眼,大家见笑了。
树也是一种无向无环图,所以DFS和BFS对于树的遍历也是适用的。
如果是树,那么对于树的DFS和DFS很简单,因为起点永远是根节点!
但是如果对于是别的二维数组或者图这样一个结构,得出所有可能的解法或者求解一个答案,我们可能就要考虑对于每一个点的DFS和BFS了!
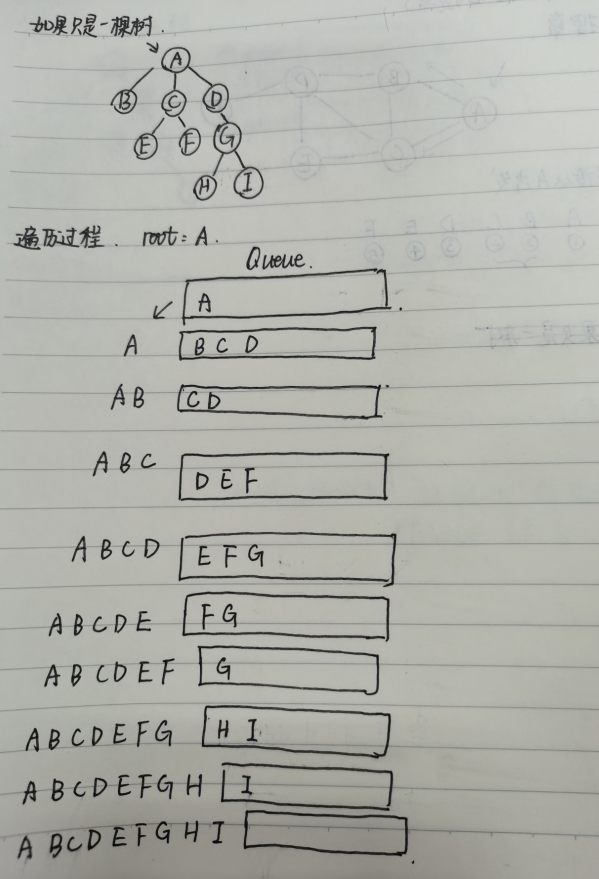
看一下树的层序遍历(BFS):
本质就是使用一个队列,初始化时,我们把根节点入队,队首用来pop()((如果是双端队列的话,那就leftpop()))出当前正在访问的节点,队尾用append()维护当前节点的左右子节点,将左右子节点加入队列:
我们首先来看一下图的上的BFS
1、图上的BFS(广度优先搜索):
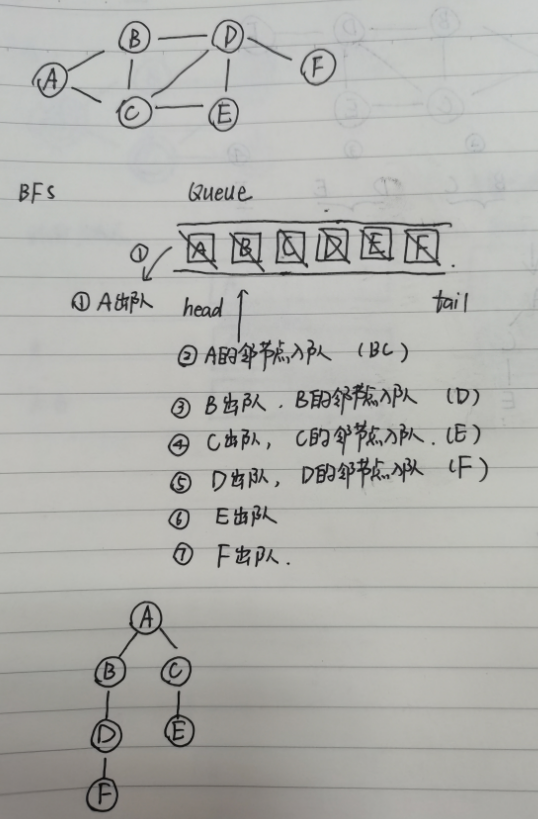
图和树的区别,就是图并没有根节点,因此我们需要选择一个节点作为我们的起始节点,以下图为例:
假设我们从A出发(距离指的是图的边的数量)
第一层为A
第二层的元素,是和A距离为1的点,B和C
第三层的元素,是和A距离为2的点,D和E
第四层的元素,是和A距离为3的点,F
那我我们可以得到一个顺序:ABCDEF
如果BC变为了CB,得到的结果还正确吗?
如果DE变为了ED,得到的结果还正确吗?
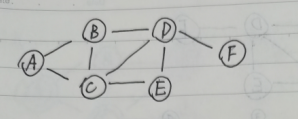
BFS,实际上是通过队列来实现的
队列初始化时,将A加入队列
遍历第一层时,将A从队首移出,和A直接相连的BC(邻接点入队)加入到队列中,假设先加入的是B,后加入的是C
遍历第二层时,此时B处于队首,那么我们也是先将B从队首移出,还要维护和B直接相连的三个点A,C,D,A已经被遍历过了,C已经在队列中了,D加入队列是没问题的,那么A和C又要怎么处理呢?
由此可见我们像树那样,找一条路径,仅仅只是用一个队列来维护我们的遍历是不够的,这里就可以看出,我们还需要一个很重要的东西来决定,我们当前是否需要对一个点进行搜索,我的理解是一个状态
状态,状态,状态!和使用BFS和DFS解题有很大的关系,对于我来说,暂时还是只可意会不可言传,晚点填坑,万一哪天我突然悟了我就能和你们讲清楚了
首先这个状态,可能是决定你是否要对当前的访问点进行搜索
其次,这个状态,可能是用来维护你访问到当前节点所产生的结果,用于得出你的答案
继续说我们把队首B移出,图上可见,E和B是不直接相连的,先不管我们的ACD要不要入队,如何入队,反正E肯定不会在D之前先入队
如果把和A相连的B和C的入队顺序变为CB,C出队时,D和E是C直接相连的,此时的DE和ED就没有区别,所以BC顺序相反,不会对后面的访问路径产生影响
如果维持了BC的顺序,那么就不可能是ED这样一个访问顺序,相应的结果也就是错误的
队列,是用来保证层的顺序,队列就是这样一种先进先出的数据结构
代码实现:
# 构造一个图 graph = { 'A': ['B', 'C'], 'B': ['A', 'C', 'D'], 'C': ['A', 'B', 'D', 'E'], 'D': ['B', 'C', 'E', 'F'], 'E': ['C', 'D'], 'F': ['D'], } # # 图上有多少个节点 # print(graph.keys()) # # 如何访问一个节点的相邻节点 # print(graph['E']) def BFS(graph, s): """ 用一个队列 queue = [] 存放所有需要被访问的节点,是一个动态数组 # queue.append(), 加入队尾 # queue.pop(0), 从队首移出 :param graph: :param s: :return: """ queue = [s] # 把起始点放入队列 seen = {s} # 用来维护当前已经被访问过的节点 res = [] # 用来存放访问的结果 while queue: # 只要队列中还存在节点, 每次循环就从里面拿一个节点 cur = queue.pop(0) # cur节点为从队首取出的当前节点 nodes = graph[cur] # 获取cur节点的邻接点 for node in nodes: # 对于所有的邻接点 if node not in seen: # 当这个节点没有被访问过 queue.append(node) # 就把这个节点入队 seen.add(node) # 维持这个节点已经被访问 res.append(cur) return res print(BFS(graph, 'A'))
2、图上的DFS(深度优先搜索)
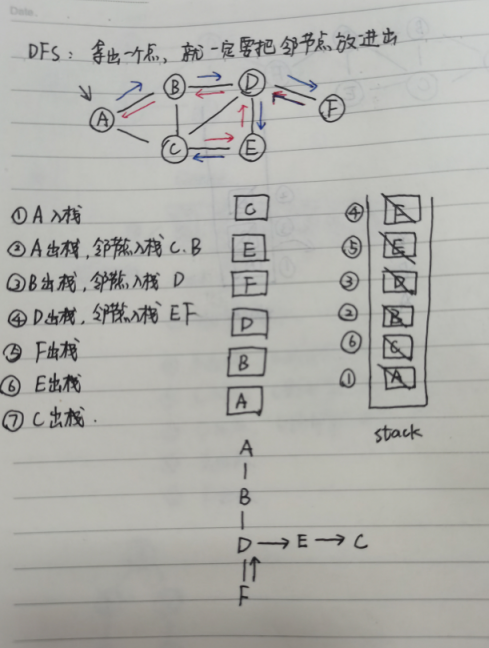
假设我们从A出发,DFS会随便找一条路(前提是有相邻路径的),一直走到底,走到不能走为止,在往回走
从A出发,有两条路可以走,一条是B,一条是C
走B,在B上往前走,可以走的路由A,C,D,A已经走过了,C和D中选一条
走D,在点D有B、C、E、F可以选择,B已经走过了,C、E、F中选一条,
走F,在点F,发现已经没有路可以走了,那么就只能往回在跳到上一个走的点D
回到点D,还是一样的选择,但是F走过了,B走过了,那没有哦走过点点就是C和E,那就在C和E之间选一条
走E,在点E有C、D可以选择,D已经走过了,那就只剩下C没有走过
走C
所以DFS真正的遍历顺序为:ABDF(D)EC(EDBA),括号中表示回退的点
DFS和递归一样都是栈结构,但是两者有很大的区别,递归是实现DFS的一个工具
DFS是通过栈来实现的
# 构造一个图 graph = { 'A': ['B', 'C'], 'B': ['A', 'C', 'D'], 'C': ['A', 'B', 'D', 'E'], 'D': ['B', 'C', 'E', 'F'], 'E': ['C', 'D'], 'F': ['D'], } def DFS(graph, s): """ 使用一个栈 stack 来模拟DFS对于每个节点访问 stack.pop() 从栈顶移除元素 stack.append() 把元素入栈(栈顶) :param graph: :param s: :return: """ stack = [s] seen = {s} res = [] while stack: cur = stack.pop() res.append(cur) nodes = graph[cur] for node in nodes: if node not in seen: stack.append(node) seen.add(node) return res print(DFS(graph, 'A'))
3、一点点扩展:
在遍历每个节点时,可以构造一个映射关系,表示这个点的前一个节点(parent)是谁,用来得出一个点到另一点的最短路径
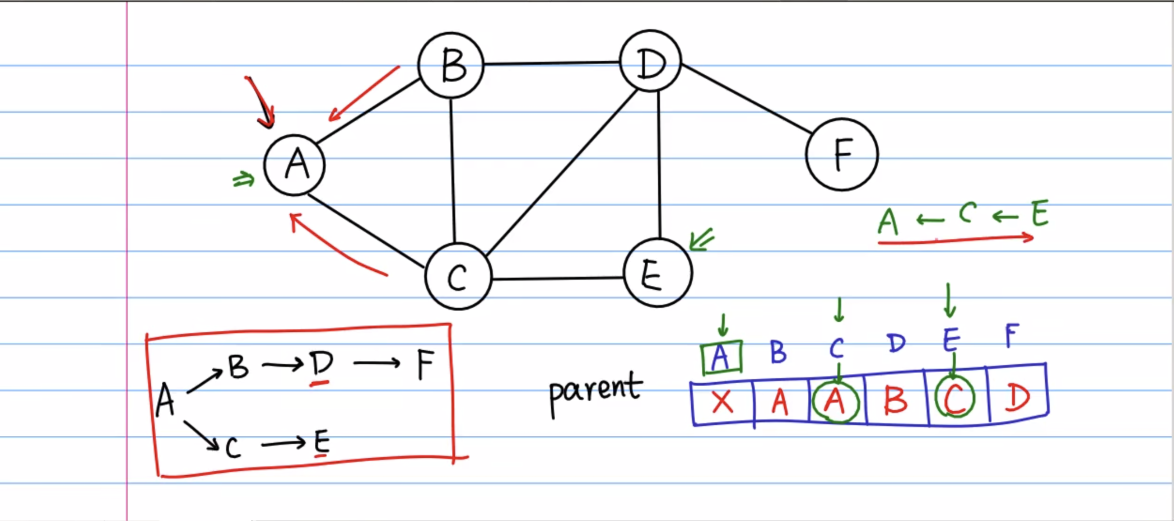
# 构造一个图 graph = { 'A': ['B', 'C'], 'B': ['A', 'C', 'D'], 'C': ['A', 'B', 'D', 'E'], 'D': ['B', 'C', 'E', 'F'], 'E': ['C', 'D'], 'F': ['D'], } # # 图上有多少个节点 # print(graph.keys()) # # 如何访问一个节点的相邻节点 # print(graph['E']) def BFS(graph, s): """ 用一个队列 queue = [] 存放所有需要被访问的节点,是一个动态数组 # queue.append(), 加入队尾 # queue.pop(0), 从队首移出 :param graph: :param s: :return: """ res = [] # 用来存放访问的结果 queue = [s] # 把起始点放入队列 seen = {s} # 用来维护当前已经被访问过的节点 parent = {s: None, } # 构造当前访问的节点的上一个节点是谁(parent) while queue: # 只要队列中还存在节点, 每次循环就从里面拿一个节点 cur = queue.pop(0) # cur节点为从队首取出的当前节点 nodes = graph[cur] # 获取cur节点的邻接点 for node in nodes: # 对于所有的邻接点 if node not in seen: # 当这个节点没有被访问过 queue.append(node) # 就把这个节点入队 seen.add(node) # 维持这个节点已经被访问 parent[node] = cur # 当前节点, 是它所有邻接点的前一个节点 res.append(cur) return parent # print(BFS(graph, 'A')) # for key, value in BFS(graph, 'A').items(): # print(key, value) node = 'B' while node: print(node) node = BFS(graph, 'A')[node]
4、再再再来亿点点的扩展!!!
一个BFS的应用:Dijkstra算法
同样也是在图上求一个最短的距离,不过现在每条边都会有一个权值,代表着距离。
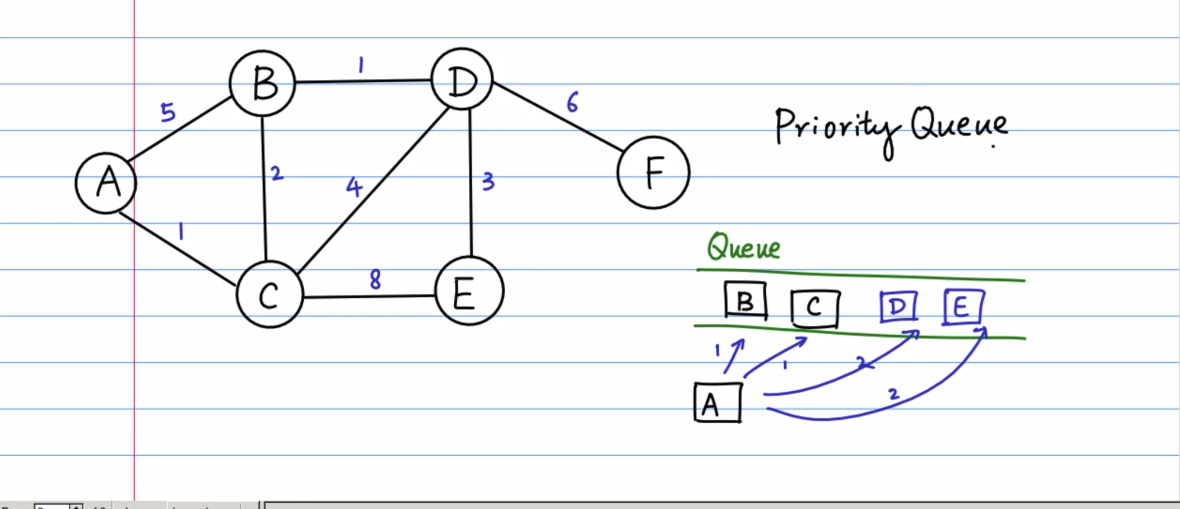

BFS本身还是通过队列来实现的,不过这里是使用了一种特殊的数据结构,堆(heap),也是最小堆,最小堆是一个什么样的东西,请移步我的另外另外一片文章,相信我已经很努力的再把它讲清楚了,一点浅薄的认知和使用,多包涵。
假设现在我们从A开始入队(A, 0),并且出队,他的领节点要进行入队,现在入队时同样也要带上一个权值(priority),这个priority就是与初始节点的距离
现在入队的两个领节点分别是(B, 5),(C, 1),这是,基于两个点所带的权值,最小堆会维护自身的性质,(C, 1)会自动调整到(B, 5)的前面
需要记住的一点是,这个priority,始终维持的是从点A出发到当前节点的距离
所以如果到D,那么入队的就是(D, 5),而不是(D, 4)
还有与普通队列非常非常有区别的一点,C的邻接点是A,B,E,在我们的普通队列中,访问到C之后,B已经存在与队列中了,那就不需要再对B做任何处理,但是,在这里不同,我们需要重新确认B通过当前出队的点C,到达A的距离,是不是比直接从A到达的那个priority要小
A -> C -> B:3
A-> B : 5
从图上的权值可知,我们对于B的的状态也是要重新更新的,并且还需要维护,到达B走过的前一个节点,不再是A,而变成了C
对于已经在队列中的(B, 5),不需要做任何改变,而是在队尾再入队一个(B, 3),根据最小堆的性质,这个新入队的(B, 3),会自动调整到队首
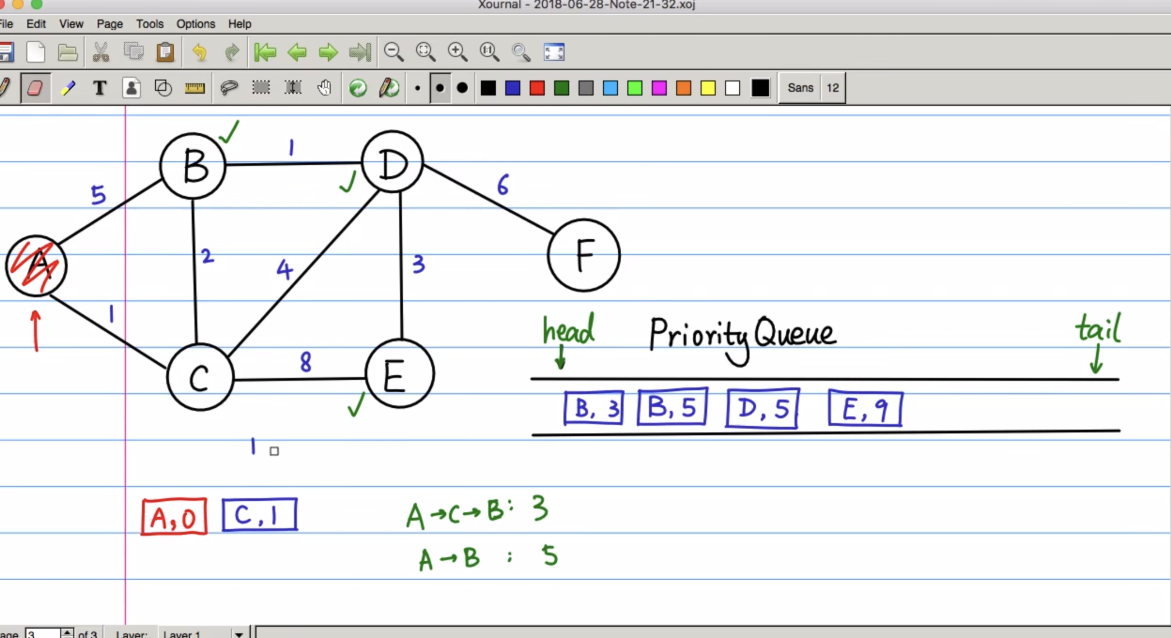
有资格出队的点(A和C)才是真正走过的点,而队列中的点,都是待处理的点
现在当B出队,那么和B直接相连的点A, C, D,其中A和C已经被访问过,就只剩下D还要被处理,那么(D, 4)入队,由于权值最小,自动调整到队首,准备下一个出队,并且出队时更新D的前一个parent为B
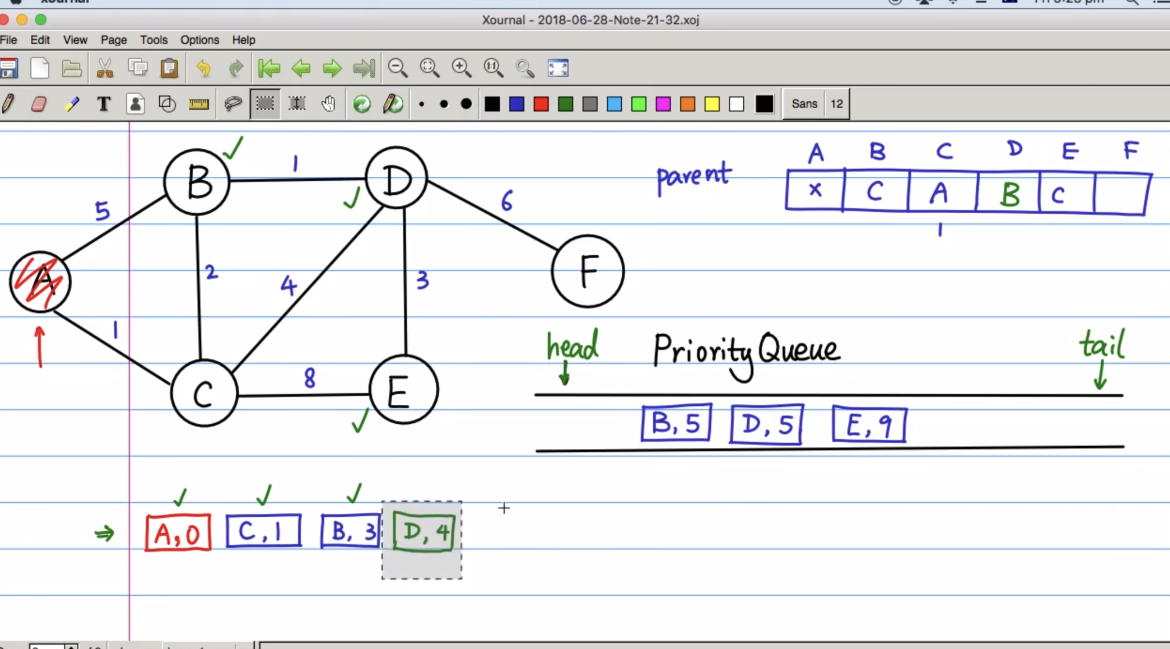
再次出队,入队,并且进行调整
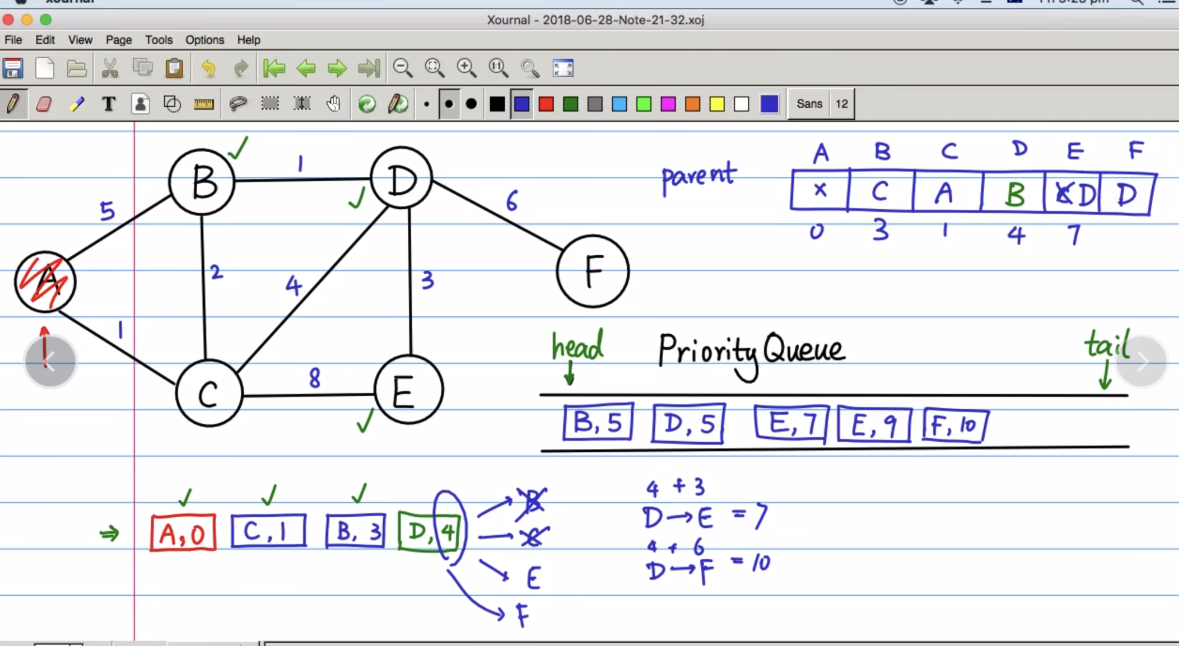
接下来出队的是B和D,但是B和D已经被访问过了,因此可以直接丢弃,然后到E出队
最后到F
最后队列为空时,最短路径也就确定了,去parent这个数据结构中去找
所以完成的访问结果如下:
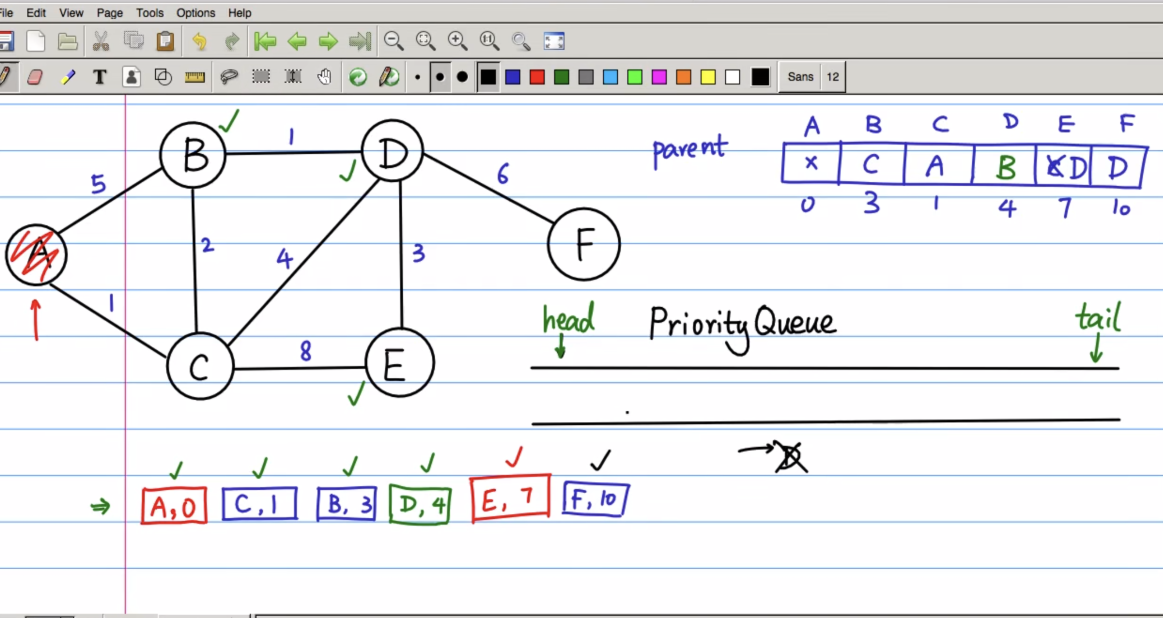
所以A到F的最短路径为:
ACBDF
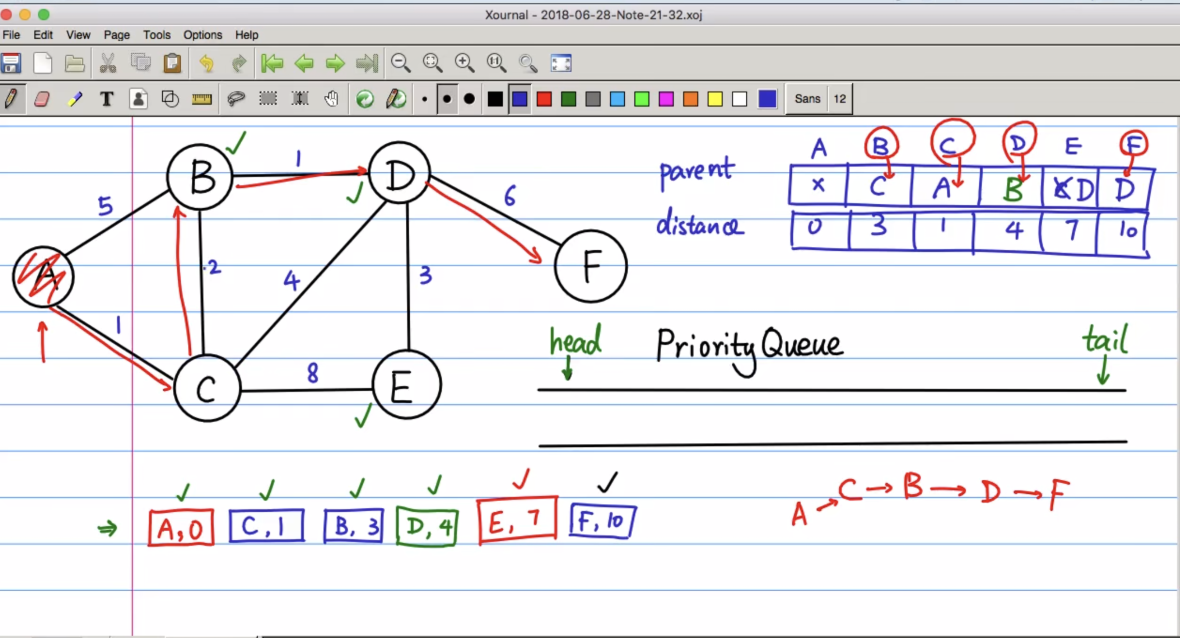
先来看一下堆
import heapq pqueue = [] heapq.heappush(pqueue, (1, 'A')) heapq.heappush(pqueue, (7, 'B')) heapq.heappush(pqueue, (3, 'C')) heapq.heappush(pqueue, (6, 'D')) heapq.heappush(pqueue, (2, 'E')) print(heapq.heappop(pqueue)) print(heapq.heappop(pqueue)) print(heapq.heappop(pqueue))
再来写一下代码,这里需要处理很多数据结构,并且数据的处理,队列的维护,都要做亿些些改变,并且,路径长度在进行初始化时,要设置为正无穷
这里的状态有[节点没有被访问过], [节点的有最短的路径]两个状态需要维护,并且这两个状态也是邻节点入队是需要维护的
import heapq # 因为要用到堆结构,所以需要import heapq # 修改一下图的结构, 增加priority graph = { 'A': {'B': 5, 'C': 1}, 'B': {'A': 5, 'C': 2, 'D': 1}, 'C': {'A': 1, 'B': 2, 'D': 4, 'E': 8}, 'D': {'B': 1, 'C': 4, 'E': 3, 'F': 6}, 'E': {'C': 8, 'D': 3}, 'F': {'D': 6}, } # # 查看一下'A'和'B'的距离 # print(graph['A']['B']) # # 仅仅拿到某一个节点的邻节点,不包括距离 # print(graph['A'].keys()) # 当A的邻节点C需要入栈时,会发现在原先distance中没有可以比较的值,因此需要对distance中所有的值进行初始化 def init_distance(graph, s): distance = {s: 0} for node in graph: if node != s: distance[node] = 1 << 60 return distance def dijkstra(graph, s): """ 使用最小堆来维持遍历每个点访问的先后顺序 import heapq hqueue = [] heapq.heappush(hqueue, (0, s)) :param graph: :param s: :return: """ hqueue = [] heapq.heappush(hqueue, (0, s)) # 准备一个堆用来遍历 seen = set() # 当一个点出队时(在最小堆调整之后), 才可以认为被访问过 parent = {s: None} # 同样,在出队之后,才会更新邻节点的上一个节点 distance = init_distance(graph, s) # 始终维护被访问过的节点到其它节点的最短距离, 需要进行初始化 while hqueue: pair = heapq.heappop(hqueue) # 此时拿出来的是一个元组,再去构造访问的点和距离 dis = pair[0] # 获取当前访问点的距离 cur = pair[1] # 获取当点被访问的节点 seen.add(cur) # 当有一个节点出队时,才认为被访问过,所以放放在这里进行初始化 nodes = graph[cur].keys() # 获取当前节点的邻节点 for node in nodes: # 如果当前节点没有被访问过,要做维护的状态有点多 # 首先如果从刚出队的节点的邻节点到当前节点的距离+dis(已知到当前节点的距离)的距离之和要比已知的距离短 # 那么需要更新, parent, distance if node not in seen: if dis + graph[cur][node] < distance[node]: # 如果 heapq.heappush(hqueue, (dis + graph[cur][node], node)) # 维护好距离之后,进行入队操作 parent[node] = cur # 根据最小的距离更新邻节点的上一个节点 distance[node] = dis + graph[cur][node] # 更新最短距离 return parent, distance if __name__ == "__main__": parent, distance = dijkstra(graph, 'A') print(parent) print(distance)
本文参考:B站UP主正月点灯笼