Sumsets
Time Limit : 4000/2000ms (Java/Other) Memory Limit : 400000/200000K (Java/Other)
Total Submission(s) : 4 Accepted Submission(s) : 3
1) 1+1+1+1+1+1+1
2) 1+1+1+1+1+2
3) 1+1+1+2+2
4) 1+1+1+4
5) 1+2+2+2
6) 1+2+4
Help FJ count all possible representations for a given integer N (1 <= N <= 1,000,000).
1) 模型和数据结构就不说了
2) 算法。以S(n)表示数n的表示方法数。虽然直觉告诉你很可能是动态规划,但第一步肯定是找规律,可能是动态规划,也可能只是普通的一个表达式而已。这里说一下找规律的感想:思维总是趋向于无序状态,所以处理问题一定要有原则,否则大脑就东想西想找不到入口(当然锻炼久了,思维习惯了有序思考就不觉得这是个很重要的问题),找规律的原则就是:一定要“动静结合”!静,就是枚举多个状态出来,直接找他们之间的规律;动,就是从当前状态,改变条件,体!会!状态是如何变化到下一种状态的,这对找规律很有帮助。往往只借助“静”的方法是“看”不出规律的,规律蕴含在变化之中。
首先,找到以例题那种方式枚举一个数的所有可能的表示方法的规律,这里略过。
其次,寻找两个数的表示方法数之间的规律。很明显可以发现n是奇数的时候,S(n)=S(n-1)
当n是偶数的时候呢?观察n从7到8的变化过程。 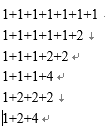
7到8,就是在7的基础上加一个1,现在把1加上去:注意,加上1之后就可以变化了! 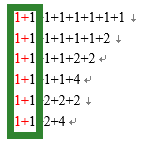
加的这个1,可以和原来奇数中单出来的1组合成2!整理下如下图所示: 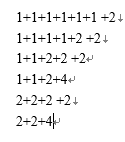
嗯,下一步该怎么办?应该找n=7和n=8的关系吧。但是这样好像不好找啊,有点乱,把合并成的2放到右边,似乎不对。例如第二到第三行的变化是不符合枚举规律的。那尝试一下不急着合并呢,不合并的话,为了满足枚举规律,只能将两个1放在最左边了。并且在枚举过程中,越靠近左边的元素是越靠后被合并的。也就是说加不加这个1上去,从开始一直合并到图二那个状态的过程是一样的,可以看到每一步都是符合枚举规律的,也就是说可以继续合并下去! 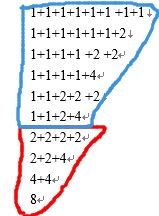
这就得到了n=8的枚举!关键是,它是从n=7的状态,通过改变条件(加1),得到的。所以,可以大胆假设当n是偶数的时候S(n)=S(n-1)+f(n)。f(n)就是下面的那个三角形。
下面考虑下面那个三角形。它的行数一定跟n有关系吗?大胆假设有,所以行数参数是n。当然,单独研究它的话,要想到把问题简单化。都除以2试一试。 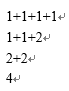
很容易发现,这是n=4的枚举。
因此,S(n)=S(n-1)+S(n/2)。
最后检验,正确。
1 #include <iostream> 2 #include <cstring> 3 #include <string> 4 #include <algorithm> 5 #define mod 1000000000 6 using namespace std; 7 long long dp[1000005]; 8 int main() 9 { 10 long long n; 11 cin >> n; 12 long long i; 13 memset(dp, 0, sizeof(dp)); 14 dp[0] = 1; 15 for (i = 1; i <= n; i++) 16 { 17 if (i * 2 == 1) dp[i] = dp[i - 1]%mod; 18 else dp[i] = (dp[i - 2] + dp[i / 2])%mod; 19 } 20 cout << dp[n] << endl; 21 return 0; 22 }