
这其实是道打表题……你看我代码就知道了……
咳咳来点严谨证明好了……
前方高能请注意
首先,正多边形近似于圆,可以看做在圆里内接多边形。圆内接多边形最多只有三个锐角。因为凸多边形的外角和为(360)度,如果有大于等于(4)个锐角,那么有大于等于(4)个外角大于(90)度,外角和肯定大于(360)度,矛盾(话说我当时只猜想出了结论不知道怎么证明……初中数学全还给老师了→_→)
那么分情况讨论(k=0,1,2,3)的情况就好了。顺便注意(n)为奇数,所以不可能存在直角的情况
k=3
此时,这个多边形肯定是三角形,所以如果(m
eq 3)无解。(因为我证不来所以就当做是显然好了)所以这里可以容斥,用总的三角形个数减去钝角三角形的个数
对于钝角三角形,三个点肯定在直径的同一侧,我们可以枚举两个点,然后第三个点肯定在这两个点在圆上较短的那条圆弧上,且上面任意一个点与这两个点组成的三角形都是钝角
从下图中不难看出,直径一边的点数最多为(leftlfloorfrac{n}{2}
ight
floor+1)

于是我们可以枚举每一个点然后逆时针枚举第二个点,那么当第二个点每逆时针走一格,第三个点能选的位置也相对应增加一个。而第三个点最多能选的位置是(leftlfloorfrac{n}{2}
ight
floor-1)(减去位于两端的第一第二个点),那么对于这一个点它能形成的钝角三角形就是(sum_{i=1}^{leftlfloorfrac{n}{2}
ight
floor-1}i),用等差数列求和公式求和,然后再乘上(n)就是总的钝角三角形个数,用总的三角形个数减去它就是锐角三角形个数了
k=2
首先,如果一个角是锐角,那么与这个点(i)相邻的两个点,他们不经过(i)的那段圆弧必定小于周长的一半。其次,不难发现如果(k=2),那么两个锐角相对应的点必定在多边形上相邻
于是我们可以枚举锐角相对应的点,设为(A,B),如果下图所示,剩下的点只有落在紫色区域才能使(A,B)都是锐角且不存在第三个锐角(如果(m>3)都行,如果(m=3)只能在上面那块紫色区域)
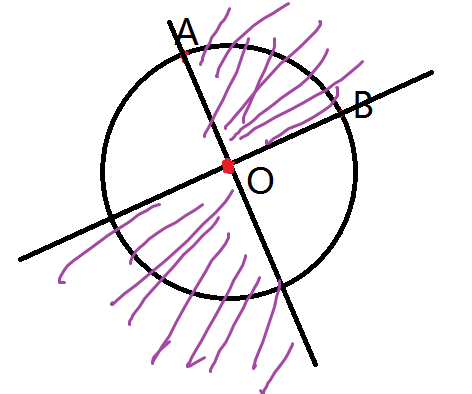
于是照例枚举(A)并逆时针枚举(B),设(AB)之间有(k)个点(不包括(A,B)),即上面那个紫色区域里可选的点有(k)个,易知下面那块紫色区域可选的点为(k+1)个(可选的点都是在正(n)边形上的)。上面那块紫色区域,(k)最大为(leftlfloorfrac{n}{2} ight floor-1),于是每一个(A)上面那块紫色区域的贡献就是(sum_{i=1}^{leftlfloorfrac{n}{2} ight floor-1}C_{i}^{m-2}=C_{leftlfloorfrac{n}{2} ight floor}^{m-1})。如果(m eq 3)就把下面那一块的贡献也加上去。最后将贡献乘上(n)就是每一个点的贡献了
这里顺便说一下形如(sum_{i=1}^nC_{i}^m)的东西怎么求和。把它拆出来,前面加上(C_{0}^m)和(C_{0}^{m+1})(这两个都等于(0))。于是原式为(C_0^{m+1}+C_0^m+C_{1}^m+C_2^m+...+C_n^m=C_1^{m+1}+C_1^m+...),然后不断合并前两项,得到(C_{n+1}^{m+1})
k=1
这种情况很麻烦,我们要保证除了枚举的点其它都不是锐角。可以按下图所示的方案来,枚举锐角(A),设(E,F)为剩下所有点的两个边界,那么(EF)不经过(A)的那段圆弧的长必定小于圆周长的一半。我们要保证(E,F)所对的两个角不是锐角,设(C,D)为与(E,F)相邻的第一个点,只有在(C)和(E),(F)和(D)都在如图直径的同一侧时,才能保证(E,F)都是钝角
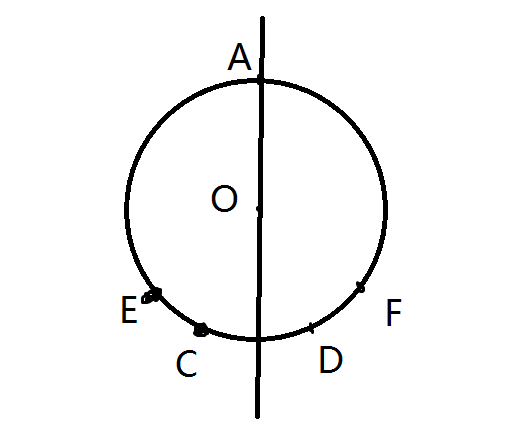
于是我们可以枚举(C,D),则(C,D)必在这条直径的两侧,我们可以枚举(C,D)之间的点数(k)(不包含(C,D)),设(T=leftlfloorfrac{n}{2} ight floor+1)(即直径的一边最多能有的点数),则(k)的上界为(T-4),对于每一个(k),考虑(C,D)的放法,共有(k+1)种,对于每一种(C,D)的放法,因为(E,F)之间包含(E,F)的点数最多为(T),所以当(E)逆时针移动时,(F)能放的位置也逆时针移动,且每次增加(1),当(E,C)在正(n)边形上相邻时,(F)能放的位置为(T-k-3),于是(E,F)放置的方案数为(sum_{i=1}^{T-k-3}i)(先别用等差数列求和公式化掉)
综上,对于每一个作为锐角的点,可行的方案数为$$Ans=sum_{k=0}^{T-4}C_{k}^{m-5}(k+1)sum_{i=1}^{T-k-3}i$$
然后答案乘上个(n)就是总的方案数。顺便从上式看出如果(m<5)无解
然而上式的计算是(O(n))的,太慢
考虑变换求和顺序,有$$Ans=sum_{i=1}^{T-3}isum_{k=0}^{T-i-3}C_{k}^{m-5}(k+1)$$
考虑形如(sum_{i=0}^n (i+1)C_i^m)的东西,有$$sum_{i=0}^n (i+1)C_i^m=sum_{i=0}^nfrac{(i+1)!}{(m+1)!(m-i)!}(m+1)$$
则这玩意儿等于((m+1)sum_{i=0}^nC_{i+1}^{m+1}),再按照(k=2)那个时候最下面说的化一下,又等于((m+1)C_{n+2}^{m+2})
于是$$sum_{k=0}^{T-i-3}C_{k}^{m-5}(k+1)=(m-4)C_{T-i-1}^{m-3}$$
原式变为$$Ans=(m-4)sum_{i=1}^{T-3}i imes C_{T-i-1}^{m-3}$$
当(T-i-1<m-3)时组合数为(0),所以可以写成$$Ans=(m-4)sum_{i=1}^{T-m+2}i imes C_{T-i-1}^{m-3}$$
考虑后面那一坨东西,令(M=m-3),展开之后为(C_{T-2}^M+2C_{T-3}^M+...+(T-M-1)C_M^M)
我们可以在后面加上一堆(C_{i}^M(i<M))反正都等于(0),于是上式可以化为(C_{T-1}^{M+1}+C_{T-2}^{M+1}+...+C_{M+1}^{M+1}=C_{T}^{M+2})
综上(k=1)时每一个点的答案为(Ans=(m-4)C_T^{m-1})
k=0
只要用所有的情况减去锐角分别为(1,2,3)的情况就好了
//minamoto
#include<cstdio>
#include<cmath>
#include<cstring>
#include<iostream>
#define R register
#define fp(i,a,b) for(R int i=a,I=b+1;i<I;++i)
#define fd(i,a,b) for(R int i=a,I=b-1;i>I;--i)
#define go(u) for(int i=head[u],v=e[i].v;i;i=e[i].nx,v=e[i].v)
char buf[1<<21],*p1=buf,*p2=buf;
inline char getc(){return p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++;}
int read(){
R int res,f=1;R char ch;
while((ch=getc())>'9'||ch<'0')(ch=='-')&&(f=-1);
for(res=ch-'0';(ch=getc())>='0'&&ch<='9';res=res*10+ch-'0');
return res*f;
}
char sr[1<<21],z[20];int K=-1,Z=0;
inline void Ot(){fwrite(sr,1,K+1,stdout),K=-1;}
void print(R int x){
if(K>1<<20)Ot();if(x<0)sr[++K]='-',x=-x;
while(z[++Z]=x%10+48,x/=10);
while(sr[++K]=z[Z],--Z);sr[++K]='
';
}
const int N=1e6,P=1000109107,inv2=500054554;
inline int add(R int x,R int y){return x+y>=P?x+y-P:x+y;}
inline int dec(R int x,R int y){return x-y<0?x-y+P:x-y;}
inline int mul(R int x,R int y){return 1ll*x*y-1ll*x*y/P*P;}
int ksm(R int x,R int y){
R int res=1;
for(;y;y>>=1,x=mul(x,x))if(y&1)res=mul(res,x);
return res;
}
int fac[N+5],inv[N+5];
int n,m,k,res;
inline int calc(R int n){return 1ll*n*(n/2)%P*(n/2-1)%P*inv2%P;}
inline int C(R int n,R int m){if(m>n)return 0;return 1ll*fac[n]*inv[m]%P*inv[n-m]%P;}
void init(){
inv[0]=fac[0]=1;fp(i,1,N)fac[i]=mul(fac[i-1],i);
inv[N]=ksm(fac[N],P-2);fd(i,N-1,1)inv[i]=mul(inv[i+1],i+1);
}
int calc3(){
if(m!=3)return 0;
int res=C(n,3);
res=dec(res,calc(n));
return res;
}
int calc2(){
int res=C(n/2,m-1);
if(m!=3)res=add(res,C(n/2+1,m-1));
res=mul(res,n);
return res;
}
int calc1(){
if(m<5)return 0;
int res=0,T=n/2+1;
res=C(T,m-1);
res=mul(res,m-4);
return mul(res,n);
}
int main(){
// freopen("testdata.in","r",stdin);
freopen("polygon.in","r",stdin);
freopen("polygon.out","w",stdout);
int T=read();init();
while(T--){
n=read(),m=read(),k=read();
switch(k){
case 3:res=calc3();break;
case 2:res=calc2();break;
case 1:res=calc1();break;
case 0:{
res=C(n,m);
res=dec(res,calc1()),res=dec(res,calc2()),res=dec(res,calc3());
break;
}
default:res=0;break;
}print(res);
}return Ot(),0;
}