1. 线积分
线积分的对象为数值量函数,用于计算诸如“非均匀曲线质量”这样的问题。解决办法是将曲线分割成无数小段,在每个小段上质量近似不变,于是总质量就是∑ρ(xi,yi)⊿s,ρ是线密度且表示为(x,y)的函数,s是曲线长度。再想想如何计算曲线长度并将问题一般化,就可以得到二维情形下的积分式子:
(假定曲线方程为y(x),线密度为f(x,y))
∫f(s)ds = ∫f(x,y(x))sqrt(1+y'2)dx
拓展到三维,将曲线使用向量式子表示,并使用参变量,就得到:

f(x,y,z)在曲线上取值,上式中假定曲线r可写为参变量t的形式<g(t), h(t), k(t)>,并利用了ds=|v(t)|dt。
实际计算时可由曲线向量式r(t)求导得到v(t)从而得到|v(t)|。
2. 向量场积分
同济《高等数学》教材称之为对坐标的曲线积分,因为积分式最终可化为对坐标积分形式。这里我们按《托马斯微积分》的名词称之为向量场积分。这种积分可用于计算变力在曲线上做的功。在计算时取函数在向量方向的分量,积分对象为向量函数(相比之下,线积分的对象为数值量函数)。

从上式中看出,向量场上的积分也可看作被积向量在曲线切方向上的(数值)线积分。
r是曲线(位置)向量,dr是沿曲线切线方向的向量,∫F·dr就是向量场积分。

对于已知F和r的情况,使用∫F·vdt最为直观。
另,上图中r是位置向量,但dr不是(?)。
后三个式子(...=∫Mdx+Ndy+Pdz)可以这么理解:分别在各个方向计算“力”和“运动距离”的乘积然后累加。例如,M是“力”(F)在x方向的分量,而dx是“运动轨迹”(r)在x方向的瞬时分量。
3. 流量积分与环流量
流量积分有两种:沿曲线方向和垂直曲线方向。这个小节先说第一种:沿曲线方向。如果曲线是直线,速度向量又沿着曲线方向且恒定,那么沿沿曲线方向的流量就是速率|v|乘上线长度。当然一般来说曲线非直线,速度也非恒定;此时流量积分(包括环流量)使用和向量场积分相同的式子:任意方向的“流”均可分解为沿曲线的切方向与法方向;只有切方向计入沿曲线的流量,法方向的“流”对流量的影响为0。
4. 通量
通量也称为“穿过曲线的流量”,是流出与进入某曲线围成区域流量的差,因此计算时使用垂直于曲线方向(法线方向)的速度分量。如果直接计算我们需要先算曲线的法向量n然后算F·n,好在一般来说我们不需要计算曲线的法向分量(对二维情况),而直接使用下述式子:
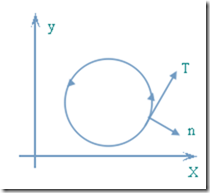
我们把一条平面曲线在某点的切分量和法分量都画一下:
上图中,法向量以小写n表示,避免与流速向量的N分量冲突。对于一个在x方向和y方向上的分量分别为dx和dy的小线段,从该线段的M方向上流出区域的量为Mdy,N方向流入区域的量为Ndx,综合起来在该线段上的总流出量就是Mdy-Ndx。上图中T和n的x分量同符号,y分量反符号,于是Mdy取正(M沿x方向),Ndx取负(N沿y方向)。
也许下面的图更加直观一点(注意环线上的箭头方向):

Mdy:流出矩形(M入左侧负向环线,出右侧正向环线)
Ndx:流入矩形(N入下侧正向环线,出上侧负向环线)
[附注:直接用F.n而不用Mdy-Ndx也是可以的;看哪个方便了。n是曲线方程标量形式f(x,y)梯度的单位化。]
5. 通量密度、散度;环量密度,旋度(k分量)
“散度”可理解为向量的“发散程度”,将x方向和y方向的发散程度(偏导)相加即得。
环量密度可以这样考虑:向量绕某点“旋转”的原因是内外流速差,N方向的内外流速差为dN/dx,M方向的流速差为-dM/dy。
6. 格林定理
[警告:以下两张图片复制自《托马斯微积分》中文版,不幸的是存在错误。当然,我相信对于你发现这个错误并不困难。]
散度是向量在区域某点的“发散”程度,在整个区域内积分就得到该区域上的通量;
旋度是向量绕区域某点的“旋转”程度,在整个区域内积分就得到该区域上的环量。
7. 积分路径无关条件
梯度场总是指向函数增长最快的方向,所以梯度场的旋度为0(既然指向增长最快方向,那么肯定“旋”不回来)。
如果某个场的旋度为0,那就表示沿该场内任意闭路径积分为0(路径无关)。
如果某个场的旋度不为0,假设这是个力场,那就表示质点可以在力总是做正功的情况下回到起点(?)。
即:旋度为0 <=> 是某标量场梯度 <=> 积分路径无关(保守场)
判断是否为保守场直接计算旋度即可。