前言
最近做的二分与三分的题目
做的好像都是板子 不是板子的题目用一种 很诡异 很巧妙的方法水了过去
1. 愤怒的牛
题意简化:
m头牛放入一条直线上的n间牛舍 最大化最小距离
思路:
二分板子
code:
/*
Time: 12.20
Worker: Blank_space
Source: #10011. 「一本通 1.2 例 1」愤怒的牛
*/
/*--------------------------------------------*/
#include<cstdio>
#include<algorithm>
using namespace std;
/*--------------------------------------头文件*/
const int A = 1e4 + 7;
const int B = 1e5 + 7;
const int C = 1e6 + 7;
const int D = 1e7 + 7;
const int mod = 1e9 + 7;
const int INF = 0x3f3f3f3f;
const int FFF = 0x8fffffff;
/*------------------------------------常量定义*/
int n, m, a[B], c[B], ans;
/*------------------------------------变量定义*/
inline int read() {
int x = 0, f = 1; char ch = getchar();
while(ch < '0' || ch > '9') {if(ch == '-') f = -1; ch = getchar();}
while(ch >= '0' && ch <= '9') {x = (x << 3) + (x << 1) + (ch ^ 48); ch = getchar();}
return x * f;
}
/*----------------------------------------快读*/
bool check(int x)
{
int sum = 0, num = 1;
for(int i = 2; i <= n; i++)
{
if(sum + c[i] < x) sum += c[i];
else {sum = 0; num++;}
}
return num >= m;
}
/*----------------------------------------函数*/
int main()
{
n = read(); m = read(); int l = 0, r = 0;
for(int i = 1; i <= n; i++) a[i] = read(), r = max(r, a[i]);
sort(a + 1, a + 1 + n);
for(int i = 1; i <= n; i++) c[i] = a[i] - a[i - 1];
while(l <= r)
{
int mid = (l + r) >> 1;
if(check(mid))
{
ans = mid;
l = mid + 1;
}
else r = mid - 1;
}
printf("%d", ans);
return 0;
}
2. Best Cow Fences
题意简化:
给定一个长度为 (n) 的非负整数序列(A) ,求一个平均数最大的,长度不小于 (L)的子段
思路:
二分平均数 将原序列中所有的数减去这个平均数 转换为判断一个子段非负 也可以说是求最大子段和
枚举到第 i 个数时 用第 i 数减去 第 1 ~ i - L 个数中最小值 统计最大值
因为已经减去了平均值 所以最后判断这个最大子段和是否非负
code:
/*
Time: 12.20
Worker: Blank_space
Source: #10012. 「一本通 1.2 例 2」Best Cow Fences
*/
/*--------------------------------------------*/
#include<cstdio>
#include<algorithm>
using namespace std;
/*--------------------------------------头文件*/
const int A = 1e4 + 7;
const int B = 1e5 + 7;
const int C = 1e6 + 7;
const int D = 1e7 + 7;
const int mod = 1e9 + 7;
const int INF = 0x3f3f3f3f;
const int FFF = 0x8fffffff;
/*------------------------------------常量定义*/
int n, L;
double a[B], b[B], sum[B];
/*------------------------------------变量定义*/
inline int read() {
int x = 0, f = 1; char ch = getchar();
while(ch < '0' || ch > '9') {if(ch == '-') f = -1; ch = getchar();}
while(ch >= '0' && ch <= '9') {x = (x << 3) + (x << 1) + (ch ^ 48); ch = getchar();}
return x * f;
}
/*----------------------------------------快读*/
bool check(double x)
{
double ans = -INF, minn = INF;
for(int i = 1; i <= n; i++) b[i] = a[i] - x, sum[i] = sum[i - 1] + b[i];
for(int i = L; i <= n; i++)
{
minn = min(minn, sum[i - L]);
ans = max(ans, sum[i] - minn);
}
return ans > 0;
}
/*----------------------------------------函数*/
int main()
{
n = read(); L = read();
for(int i = 1; i <= n; i++) a[i] = read();
double eps = 1e-5, l = -1e6, r = 1e6;
while(r - l > eps)
{
double mid = (l + r) / 2;
if(check(mid)) l = mid;
else r = mid;
}
printf("%d", int(r * 1e3));
return 0;
}
3. 曲线
题意简化:
求n个二次函数在区间[1, n]上的最大值
思路:
三分板子
code:
/*
Time: 12.20
Worker: Blank_space
Source: #10013. 「一本通 1.2 例 3」曲线
*/
/*--------------------------------------------*/
#include<cstdio>
#include<algorithm>
#include<string.h>
#define emm(x) memset(x, 0, sizeof x)
using namespace std;
/*--------------------------------------头文件*/
const int A = 1e4 + 7;
const int B = 1e5 + 7;
const int C = 1e6 + 7;
const int D = 1e7 + 7;
const int mod = 1e9 + 7;
const int INF = 0x3f3f3f3f;
const int FFF = 0x8fffffff;
/*------------------------------------常量定义*/
int T, n;
struct node {
double a, b, c;
}a[B];
/*------------------------------------变量定义*/
inline int read() {
int x = 0, f = 1; char ch = getchar();
while(ch < '0' || ch > '9') {if(ch == '-') f = -1; ch = getchar();}
while(ch >= '0' && ch <= '9') {x = (x << 3) + (x << 1) + (ch ^ 48); ch = getchar();}
return x * f;
}
/*----------------------------------------快读*/
double f(double x)
{
double _ans = -INF;
for(int i = 1; i <= n; i++) _ans = max(_ans, a[i].a * x * x + a[i].b * x + a[i].c);
return _ans;
}
void work()
{
n = read(); emm(a); double l = 0, r = 1000;
for(int i = 1; i <= n; i++) {a[i].a = read(); a[i].b = read(); a[i].c = read();}
while(l + 1e-10 < r)
{
double m1 = l + (r - l) / 3, m2 = r - (r - l) / 3;
if(f(m1) > f(m2)) l = m1;
else r = m2;
}
printf("%.4f
", f(l));
}
/*----------------------------------------函数*/
int main()
{
T = read();
while(T--) work();
return 0;
}
4. 数列分段II
题意简化:
长度为(n)的正整数数列 分为连续m段 最小化每一段的最大值
思路:
二分每一区间的最大值 进行检查
二分答案板子
code:
/*
Time: 12.20
Worker: Blank_space
Source: #10014. 「一本通 1.2 练习 1」数列分段 II
*/
/*--------------------------------------------*/
#include<cstdio>
#include<algorithm>
using namespace std;
/*--------------------------------------头文件*/
const int A = 1e4 + 7;
const int B = 1e5 + 7;
const int C = 1e6 + 7;
const int D = 1e7 + 7;
const int mod = 1e9 + 7;
const int INF = 0x3f3f3f3f;
const int FFF = 0x8fffffff;
/*------------------------------------常量定义*/
int n, m, a[B], s, ans, maxx;
/*------------------------------------变量定义*/
inline int read() {
int x = 0, f = 1; char ch = getchar();
while(ch < '0' || ch > '9') {if(ch == '-') f = -1; ch = getchar();}
while(ch >= '0' && ch <= '9') {x = (x << 3) + (x << 1) + (ch ^ 48); ch = getchar();}
return x * f;
}
/*----------------------------------------快读*/
bool check(int x)
{
int sum = 0, num = 1;
for(int i = 1; i <= n; i++)
if(sum + a[i] <= x) sum += a[i];
else {sum = a[i]; num++;}
return num <= m;
}
/*----------------------------------------函数*/
int main()
{
// freopen("divide_b4.in", "r", stdin);
n = read(); m = read();
for(int i = 1; i <= n; i++) a[i] = read(), s += a[i], maxx = max(a[i], maxx);
int l = maxx, r = s;
while(l <= r)
{
int mid = (l + r) >> 1;
if(check(mid))
{
ans = mid;
r = mid - 1;
}
else l = mid + 1;
}
printf("%d", ans);
return 0;
}
5. 扩散
题意简化:
在一个二维空间内 给定 n 个点 一个点每过一个单位的时间就会向4个方向扩散一个距离 两个点的扩散区域有重合时称两个点联通 求n个点形成一个连通块时的最小时间
思路:
当两个点中间没有其他点时 这两个点联通的最小时间就是这两个点的曼哈顿距离除以二
由此来判断二分出的时间是否合法
对于点与点之间的联通 采用并查集来实现
code:
/*
Time: 12.20
Worker: Blank_space
Source: #10015. 「一本通 1.2 练习 2」扩散
*/
/*--------------------------------------------*/
#include<cstdio>
#include<algorithm>
using namespace std;
/*--------------------------------------头文件*/
const int A = 1e4 + 7;
const int B = 1e5 + 7;
const int C = 1e6 + 7;
const int D = 1e7 + 7;
const int mod = 1e9 + 7;
const int INF = 0x3f3f3f3f;
const int FFF = 0x8fffffff;
/*------------------------------------常量定义*/
int n, maxx, maxy, minx = INF, miny = INF, fa[100], ans, cnt;
struct node {
int x, y;
}a[100];
/*------------------------------------变量定义*/
inline int read() {
int x = 0, f = 1; char ch = getchar();
while(ch < '0' || ch > '9') {if(ch == '-') f = -1; ch = getchar();}
while(ch >= '0' && ch <= '9') {x = (x << 3) + (x << 1) + (ch ^ 48); ch = getchar();}
return x * f;
}
/*----------------------------------------快读*/
int find(int x) { if(fa[x] != x) return fa[x] = find(fa[x]); return x;}
bool check(int x)
{
for(int i = 1; i <= n; i++) fa[i] = i; cnt = 0;
for(int i = 1; i <= n; i++)
for(int j = i + 1; j <= n; j++)
if(abs(a[i].x - a[j].x) + abs(a[i].y - a[j].y) <= x * 2)
{
int xx = find(i), yy = find(j);
if(xx != yy) fa[xx] = yy;
}
for(int i = 1; i <= n; i++)
if(fa[i] == i) cnt++;
return cnt == 1;
}
/*----------------------------------------函数*/
int main()
{
n = read();
for(int i = 1; i <= n; i++)
{
a[i].x = read();a[i].y = read();
maxx = max(maxx, a[i].x); maxy = max(maxy, a[i].y);
minx = min(minx, a[i].x); miny = min(miny, a[i].y);
}
int l = 0, r = maxx + maxy - minx - miny;
while(l <= r)
{
int mid = (l + r) >> 1;
if(check(mid))
{
ans = mid;
r = mid - 1;
}
else l = mid + 1;
}
printf("%d", ans);
return 0;
}
6. 灯泡
题目描述
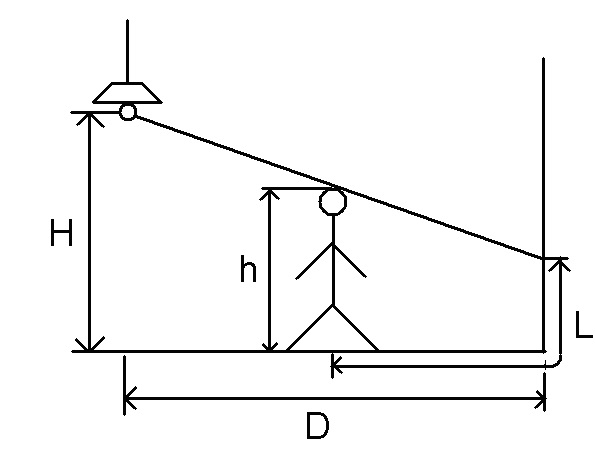
相比 wildleopard 的家,他的弟弟 mildleopard 比较穷。他的房子是狭窄的而且在他的房间里面仅有一个灯泡。每天晚上,他徘徊在自己狭小的房子里,思考如何赚更多的钱。有一天,他发现他的影子的长度随着他在灯泡和墙壁之间走到时发生着变化。一个突然的想法出现在脑海里,他想知道他的影子的最大长度。
思路:
我感觉这是个结论题
这是什么二分啊 这不就是一个数学题吗
所以用一种很 诡异 巧妙的方法水过
但我的复杂度是 (O(1)) 的
首先 根据题目:
灯高 H
人高 h
灯距墙壁的距离为 D
人的影子长度为 L
考虑表示人的影子长度
设:
人与灯的距离为 x
影子落在墙上(如果有的话)的部分为 y
墙上的那部分影子如果再落在地上所能产生的影子的长度为 t
如图:
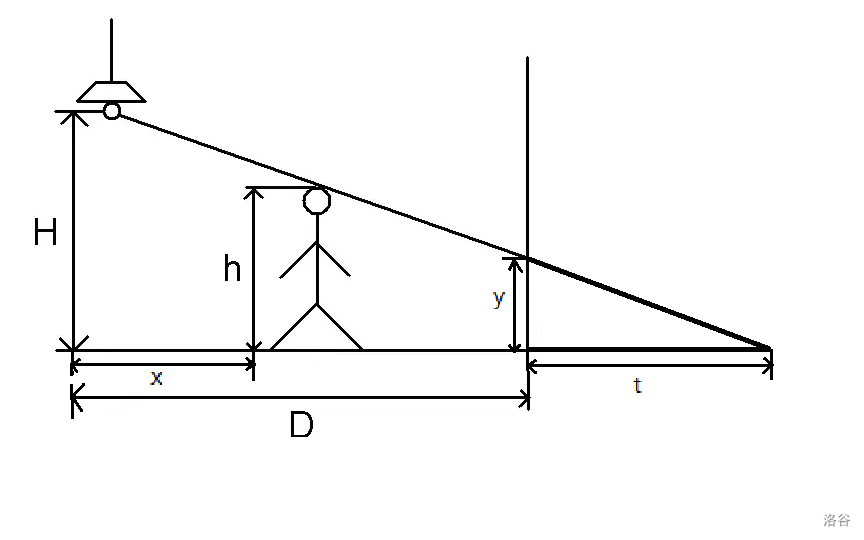
(下面的推导过程我建议把图画下来对着图理解)
然后 根据影子是否落在墙上分类讨论
一: 影子没有落在墙上
此时 根据相似三角形可以直接得出:
化简 得:
这个时候 因为要保证影子不会落在墙上 所以 有:
将 L 代入 得:
化简 得:
所以 x 的范围:
二: 影子有一部分落在墙上
由图 我们不难看出:
此时 根据相似三角形 有:
设出的为自变量 想办法让 x 进入这个式子
观察一下图 可以列出:
所以上面的式子又可以化为:
将式子拆开来看
首先是左边两个:
化简 得:
我们就有了 t 与 x 的关系
再看右边:
化简 得:
然后将 t 代入 得:
化简 得 :
x 与 y 的关系也有了
回到上面的式子:
代入 y 得:
化简 得:
结合上一种情况 此时 x 的范围为:
整理这两种情况 就有了L 关于 x 的函数:
所以有什么用呢?
上面的那个式子 很明显是单调递增的 所以最大值在右端点取到
下面的那个式子 再观察一下:
这就很明显了
后面那一坨东西就是对勾函数
那么:
所以:
当且仅当:
时 L 取到最大值
这时我们发现 这个 x 到底能不能取到是一个问题
对于这一问题 我们再次分类讨论
一:
当
时
因为前面的那个式子是单调的
所以此时的答案就为:
二:
当
时
将两个取值范围的最值进行比较 取较大值
即 比较:
的大小
三:
当
时
此时 ((0 , D]) 这一区间内 函数是单调递增的
所以最大值在 (x = D) 处取到
此时 最大值为:(h)
再与(frac{hD}{H}) 进行比较即可
至此 对于每一次的询问 则可以 (O(1)) 的进行回答
code:
/*
Time: 12.20
Worker: Blank_space
Source: #10016. 「一本通 1.2 练习 3」灯泡
要什么二分三分的 这就是个结论题
*/
/*--------------------------------------------*/
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cmath>
using namespace std;
/*--------------------------------------头文件*/
const int A = 1e4 + 7;
const int B = 1e5 + 7;
const int C = 1e6 + 7;
const int mod = 1e9 + 7;
const int INF = 0x3f3f3f3f;
const int FFF = 0x8fffffff;
/*------------------------------------常量定义*/
int T;
double H, h, D;
/*------------------------------------变量定义*/
void work()
{
cin >> H >> h >> D;
printf("%.3f
", (sqrt(D * (H - h)) < (H - h) * D / H) ? (D * h / H) : (max(h * D / H, (sqrt(D * (H - h)) > D) ? h : (D + H - 2 * sqrt(D * (H - h))))));
}
/*----------------------------------------函数*/
int main()
{
scanf("%d", &T);
while(T--) work();
return 0;
}