随机变量的分布
连续性随机变量
离散型随机变量
随机变量
实验中的各种统计的数值
离散型随机变量
随机变量并不是连续变化的
随机变量是有限个数的
连续型随机变量
随机变量是连续变化的
随机变量的个数是无限个的
概率函数
为离散型的随机变量定义的
本身为概率值, X是随机变量的取值,P为概率值
离散型随机变量的概率分布
找到的是离散型随机变量的所以可能的取值
得到的离散型随机变量的取值的概率
离散型随机变量的概率函数
连续型随机变量 概率密度
连续型的随机变量,因为其随机变量的值是连续的无法给出具体的值的概率,即无法画出概率的 分布表
故此,使用密度表示概率的分布
概率密度函数
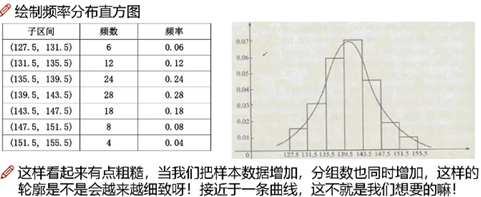
将连续值分区段,离散化,
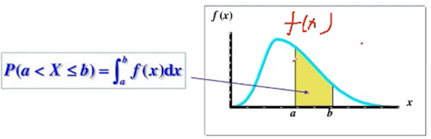
X为离散随机变量,X再任意区间的(a,b) 上的概率表示为(对该区间积分求该区域面积):
简单随机抽样 要求
抽取的样本满足:
1 样本之间是相互独立互不影响的随机变量
2 样本与总体同分布
联合分布函数:
使用累乘
联合概率密度:
似然函数
给定的联合样本值x服从关于参数θ的函数
其中x是随机变量的x的取值, θ是未知参数
似然函数的密度函数, 表示给定的θ的联合密度函数
似然函数:
有一部分观测值,会产生不同的结果, 使用θ作为参数,进行结果拟合
最终,找出参数θ
离散情况下的似然函数
即,找出在θ什么样的情况下,θ参数使得某个事件发生的概率更大

连续情况下的似然函数

概率是给定θ概率
似然是给定x求θ在什么条件下概率最大
极大似然估计

离散连续下的极大似然估计
离散样本:
连续样本:
极大似然估计:

求解的θ使得概率最大最好
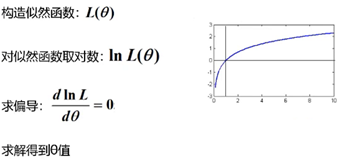
极大似然估计的求解
使用对数似然,将累乘转换为累加,求解到θ值