【转载】重新理解函数空间

重新理解函数空间(上)

读论文时遇到了可再生核希尔伯特空间。尽管之前在雁栖湖上课学习SVM时听郭嘉丰老师讲过一嘴，但还是被这个名词吓得不敢动弹。张颢老师曾说，对一些经常用到的知识要有“小脑反应”，看待这些名词都不需要经过大脑，这才是最高境界。于是下决心花一天的时间深入理解它。万幸发现了几个非常好的教程，总算是能够较为直观的理解了，这里把自己的感想写下来。

这部分内容包括一些常见的空间的定义，包括欧几里得空间，巴纳赫空间，希尔伯特空间，可再生核希尔伯特空间。理解他们以后，我们再用新的视角重新看待函数内积，傅里叶变换，小波变换和kernel SVM。

读到这里有没有觉得很害怕。在三个小时之前，我也很害怕，而理解了以后发现无非是些唬人的东西。希望看完这篇笔记，大家也可以把它们写到自己的周报或者论文里唬一下自己的老师和同学。

线性空间，距离，范数，欧几里得空间，希尔伯特空间

首先什么是空间？我们生活就在一个空间内。空间一定是由元素和他们之间的规则组成的。数学中的空间也是如此。组成空间的元素是一个个的向量，而向量之间的相互关系就是空间内的规则。我们接下来要讨论的空间无外乎都由这个基础展开，无非是规则越来越具体。

线性空间的概念相信大家已经耳熟能详了。即定义了加法和数乘的空间就是线性空间。

关于加法和数乘要满足的性质这里不予讨论。慢慢人们发现，我们需要度量V$V$中元素的相似程度，也就是需要一个距离。这个距离该满足什么条件呢？首先，自身和自身的距离应该是0，而自身和其他的距离应大于0。第二，A和B的距离与B和A的距离应该是相同的。第三，A和B的距离与B和C的距离之和要大于等于A和C的距离。满足上面这三条后才符合我们心中对距离的直观感受。

在现实世界中，最常见的距离当然是直线距离。但在地球仪上，我们往往会使用两点之间的大圆作为实际距离。因此距离的定义是多种多样的。只要满足距离的三条性质，就可以被认为是一种距离。而定义了距离以后的空间又被叫做度量空间。

有了度量空间后还不够，我们需要知道向量本身的大小。于是我们引入了范数的概念。范数同样需要满足非负性和三角不等式，但范数还有一个条件，即∥αx∥=|α|∥x∥$\Vert \alpha x\Vert =|\alpha |\Vert x\Vert$。要注意的是，第三条性质是距离所不具备的，因此范数比距离更加具体。对于构建了范数的空间，可以通过d(x,y)=∥x−y∥$d(x,y)=\Vert x-y\Vert$来导出距离，但定义了距离的空间却无法导出范数。

定义了范数的空间被称为赋范空间，也就是逼格很高的巴纳赫空间。我们自己写文章的时候也要这样，能写巴纳赫空间就绝对不要写赋范空间，这样才能吓住审稿人，提高自己的录用概率。

有了范数以后还是少了点什么，那就是夹角。对呀，我们没有定义两个向量的夹角啊。高中数学已经学习了夹角和内积的关系，因此，引入内积就可以定义夹角。内积函数需要<script type="math/tex" id="MathJax-Element-4">

</script>具有对称性，对第一变元线性和正定性。对第一变元的线性性的要求是范数所不具备的，因此内积空间比
赋范空间更具体。

定义了内积的线性空间就是欧几里得空间，我们生活的世界大概就是一个欧几里得空间了。因此欧几里得空间中的很多运算和操作都能够给我们非常直观的感受。

将欧几里得空间扩展到无穷维向量上，再加上完备性就是希尔伯特空间了。

到这里总算把这些空间的相关关系讲完了。你可能会想，无穷维向量的空间有什么用呢？一会儿你就知道，它的用处大的很。

函数空间

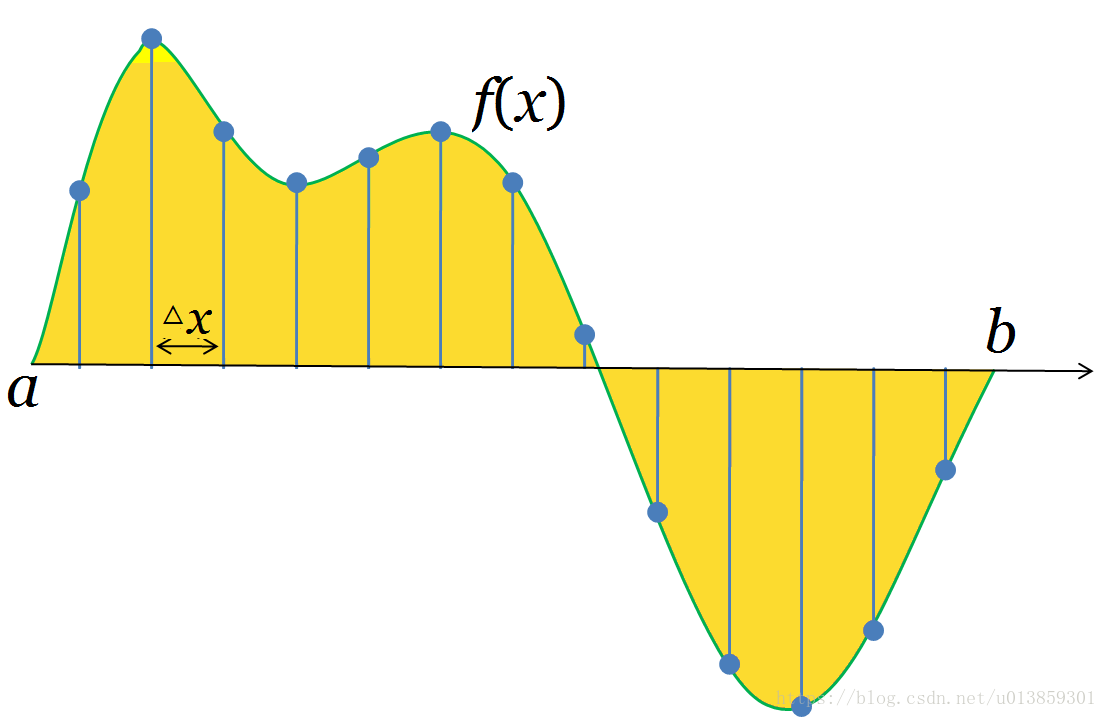
对于任意函数f(x)$f(x)$，我们都可以将其看作是一个无穷维向量。如上图所示，只要我们在函数上面以dx$dx$为间隔进行均匀采样，就可以得到一个向量。Δx$\mathrm{\Delta }x$取得越小，这个向量就越接近函数本身。当Δx$\mathrm{\Delta }x$取到无穷小时，这个无穷维向量就已经能够完全代表这个函数了。

看到了吧？我们研究的函数都可以看成是希尔伯特空间中的向量。这样一来，内积的定义也就很明确了。考虑欧几里得空间中的内积定义，

<x,y>=∑ixiyi$$<x,y>=\sum _i{x}_i{y}_i$$

函数内积可定义为

<f,g>=limΔx→0∑if(xi)g(xi)Δx=∫f(x)g(x)dx$$<f,g>=\underset{\mathrm{\Delta }x\to 0}{lim}\sum _{i}f(x_i)g(x_i)\mathrm{\Delta }x=\int f(x)g(x)dx$$

多了的 dx$dx$是因为欧几里得中的向量都是整数维，而希尔伯特空间中的维度被切割成了以 dx$dx$为单位的小片，因此需要 dx$dx$来归一化。

再回到欧几里得空间中。我们知道对于n维空间，只要确定了n个线性无关的基向量，其他向量可以由这组向量线性表出。而在希尔伯特空间中依然如此。希尔伯特空间是无穷维的，只要我们能找到无穷个线性无关的函数作为基底，其他任何函数都可以由这组函数线性表出。如果这组基之间相互正交，就构成正交基。中学时也知道，正交基的相互运算可以消掉交叉项，非常方便。所以才有了傅里叶变换和小波变换。

函数基的实例——傅里叶变换

傅里叶函数的基函数为{hp}+∞p=−∞$\{h_p{\}}_{p=-\mathrm{\infty }}^{+\mathrm{\infty }}$，其中p$p$为正整数

hp(x)=ei2πpx/T$$h_p(x)=e^{i2\pi px/T}$$

当p,q$p,q$不同时，基函数两两之间的内积为

<hp,hq>=∫T0hp(x)h¯q(x)dx=∫T0ei2πpx/Te−i2πqx/Tdx=0$$<h_p,h_q>={\int }_0^T{h}_p(x){\overline{h}}_q(x)dx={\int }_0^T{e}^{i2\pi px/T}{e}^{-i2\pi qx/T}dx=0$$

p,q$p,q$相同时

|hp|2=<hp,hp>=T$$|h_p{|}^2=<h_p,h_p>=T$$

因此任意函数 f$f$可以由这组正交基线性表出，即

f(x)=∑pcphp(x)=∑pcpei2πpx/T$$f(x)=\sum _p{c}_p{h}_p(x)=\sum _p{c}_p{e}^{i2\pi px/T}$$

而其坐标 cp$c_p$也可以由向量点积求出

cp=1T<f,hp>=1T∫f(x)h¯p(x)dx=1T∫T0f(x)e−i2πpxdx$$c_p=\frac{1}{T}<f,h_p>=\frac{1}{T}\int f(x){\overline{h}}_p(x)dx=\frac{1}{T}{\int }_0^{T}f(x)e^{-i2\pi px}dx$$

这就是傅里叶变换。

函数基的实例——小波变换

小波变换和傅里叶变换相似，只不过基底换成了

ψn,k(x)=2n/2ψ(2nx−k),x∈R$${\psi }_{n,k}(x)=2^{n/2}\psi (2^{n}x-k),x\in \mathbf{R}$$

其中，

ψ(x)=⎧⎩⎨⎪⎪1−100≤x<12,12≤x<1otherwise$$\psi (x)=\{\begin{array}{ll}1& 0\le x<\frac{1}{2},\\ -1& \frac{1}{2}\le x<1\\ 0& \text{otherwise}\end{array}$$

这组基底之间的正交性证明如下

<ψn1,k1,ψn2,k2>=∫ψn1,k1(x),ψn2,k2(x)dx={10n1=n2,k1=k2otherwise$$<{\psi }_{n_1,k_1},{\psi }_{n_2,k_2}>=\int {\psi }_{n_1,k_1}(x),{\psi }_{n_2,k_2}(x)dx=\{\begin{array}{ll}1& n_1=n_2,k_1=k_2\\ 0& \text{otherwise}\end{array}$$

篇幅所限，上半部分写到这里。后半部分将会继续介绍 可再生核希尔伯特空间以及其在SVM中的应用。

参考文献

1. songcy的博客：http://songcy.net/posts/story-of-basis-and-kernel-part-1/
2. 上海交通大学公开课《数学之旅——函数空间》：http://open.163.com/movie/2013/3/T/0/M8PTB0GHI_M8PTBUHT0.html

转载自： https://blog.csdn.net/u013859301/article/details/81710985