极限
引入极限
简单点就是趋近的数值。
比方说有 \(f(x) = \frac{x^2-1}{x-1}\),如何知道 \(f(1)\) 的值?
显然我们不能直接求,于是可以换一种方法:
趋近法。
假设我们让 \(x\) 从小到大趋近 \(1\),那么:
| \(x\) | \(f(x)\) |
|---|---|
| \(0.5\) | \(1.5\) |
| \(0.9\) | \(1.9\) |
| \(0.99\) | \(1.99\) |
| \(0.999\) | \(1.999\) |
可以知道 \(f(1)=2\) 的事实。但是我们不能说“当 \(x=1\) 时,\(f(x)=2\)”,因为 \(x\) 无法取到 \(1\).
于是我们可以这样说:
不能说 \(x=1\) 是多少,我们应说“不管那个值具体是什么,\(x\) 趋近于 \(1\) 时答案就趋近于 \(2\)”,正确理解等于号的含义。
事实上我们犯了一个错误。求极限是不能只从一边的,因为有的时候两边趋近的答案不一样。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-7FN7U9dJ-1624976567074)(https://www.shuxuele.com/calculus/images/discontinuous-function.svg)]](https://img2020.cnblogs.com/blog/1972529/202111/1972529-20211121171943085-213310698.png)
一般的极限不存在的,可见。
还有说明一个误区:哪怕那个点明确可以取到,只要符合极限的定义,就可以。你也可以说:
这没有任何问题。
无穷大
\(\infty\) 表示无穷大。但是我们需要注意一些事项。
无穷大
\(\frac{1}{\infty} = 0\),这是对的吗?
这是错的。\(\infty\) 不是数,不可以参与运算,这是无意义的。
但是我们知道一个事实:
当 \(x\) 越来越大时,\(\frac{1}{x}\) 越来越趋近于 \(0\).
但是我们无法描述“越来越大”是趋近于多少,于是引进了 \(\infty\) 来表示。
因此:
一个特殊的公式
求极限
一、代入法
很显然,对于一些函数是生效的,但是对于一大部分函数不生效。
二、因式分解法
\(\lim \limits_{x \rightarrow 1} \frac{x^2-1}{x-1} = \lim \limits_{x \rightarrow 1} (x+1)\)
再用代入法可知为 \(2\).
判断函数趋近
考虑对于 \(f(x)\),如何判断 \(x \rightarrow \infty\) 时,\(f(x)\) 趋近于 \(0,-\infty,\infty\)(也有可能是别的值)?
形如 \(\frac{1}{x}\) 的趋近于 \(0\),很好判断。
剩下的,直接看最高次系数的正负。正则趋近无穷大,负则趋近负无穷大。
如果有分母,最高次次数一致时,把分子分母最高次的系数相除就可以,这个值就是函数的趋近值(\(x\) 无穷大时)。
因此:
如果不一致,那么看系数相除的正负,同理判断趋近正(负)无穷大即可。
因此:
其实原因很简单,\(x\) 趋近无穷时,因为系数是常数,最后整式的值一定是最高次项,所以仅考虑最高次项就可以判断函数的趋近值。
严格的证明
现在我们需要考虑,如何严格证明极限的大小?先前我们给出极限的定义并不官方,而多是口语化。大家理解了之后,我们来考虑真正的极限。
数学中的“极限”指:某一个函数中的某一个变量,此变量在变大(或者变小)的永远变化的过程中,逐渐向某一个确定的数值A不断地逼近而“永远不能够重合到A”(“永远不能够等于A,但是取等于A‘已经足够取得高精度计算结果)的过程中,此变量的变化,被人为规定为“永远靠近而不停止”、其有一个“不断地极为靠近A点的趋势”。极限是一种“变化状态”的描述。此变量永远趋近的值A叫做“极限值”(当然也可以用其他符号表示)。——百度百科
假设我们现在想要描述:
- 当 \(x\) 趋近于 \(a\) 时,\(f(x)\) 趋近于 \(L\).
考虑用作差法表示“趋近”的含义。也就是:
当 \(|x-a|<\delta\) 时,\(|f(x)-L| < \epsilon\)
严格表示趋近(极限)的方式:
对于任何 \(\delta > 0\),有 \(\epsilon>0\),从而使得当 \(|x-a|<\delta\) 时,\(|f(x)-L| < \epsilon\).
看起来很复杂,实际上核心就是那一句:
- 当 \(x\) 趋近于 \(a\) 时,\(f(x)\) 趋近于 \(L\).
来个例题:证明 \(\lim \limits_{x \rightarrow 3} 2x=6\).
我们已知 \(|x-3| < \delta\).
可以得到 \(|2x-6|< 2 \delta\).
因此 \(\epsilon = 2 \delta\) 时成立,于是原式成立。
连续函数
一个函数在某点连续的判定是:
于是 \(f(x)\) 在 \(c\) 点连续。
也就是说,出现断点、非连续(渐近线)都是非连续函数。
如果一个函数对于所有 \(c\) 都满足上述式子,则为连续函数。如:
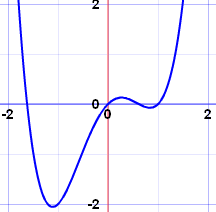
而非连续函数的例子(不连续的):
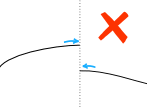
导数(微分)
导数可以被认为是函数一部分的“坡度”。
假设在某函数的某一部分 \(x\) 共增加 \(\triangle x\),\(y\) 增加 \(\triangle y\),于是该部分的导数为 \(\frac{\triangle x}{\triangle y}\). 根据这个定义还是比较好求的。用 \(\frac{d}{dx}\) 表示。
考虑一个问题:如何对函数上的某一个点求导?
\(\frac{0}{0} = ?\)
求导入门
假设对 \(f(x) = x^2\) 求导。考虑:
于是:
你发现对于一个点,\(\triangle x =0\),于是可得:
同理我们计算 \(\frac{d}{dx} x^3 = 3x^2\).
现在我们可以计算一些简单函数的导数啦!
求导进阶
现在考虑一个问题:一些函数的导数似乎不是很好求,计算相当繁琐。另外一些如:
\(\frac{d}{dx} \sin(x)\)?
就必须背公式了。
王牌公式:
| 常见函数 | 函数(\(f(x)=\)) | 导数 |
|---|---|---|
| 常数 | \(c\) | \(0\) |
| 直线 | \(ax\) | \(a\) |
| 平方 | \(x^2\) | \(2x\) |
| 平方根 | \(\sqrt{x}\) | \(\frac{1}{2} x^{-\frac{1}{2}}\) |
| 指数 | \(e^x\) | \(e^x\) |
| 指数 | \(a^x\) | \(\operatorname{In}(a) a^x\) |
| 对数 | \(\log_a x\) | \(\frac{1}{x \operatorname{In}(a)}\) |
| 对数 | \(\operatorname{In}(x)\) | \(\frac{1}{x}\) |
| 三角 | \(\sin(x)\) | \(\cos(x)\) |
| 三角 | \(\cos(x)\) | \(-\sin(x)\) |
| 三角 | \(\tan(x)\) | \(\sec^2(x)\) |
导数法则:
(用 \(f',g'\) 表示其导数)
| 法则 | 函数(\(f(x)=\)) | 导数 |
|---|---|---|
| 乘以常数 | \(cf\) | \(cf'\) |
| 幂次法则 | \(x^n\) | \(nx^{n-1}\) |
| 加(减)法法则 | \(f \pm g\) | \(f' \pm g'\) |
| 乘法法则 | \(fg\) | \(fg'+f'g\) |
| 除法法则 | \(\frac{f}{g}\) | \(\frac{f'g-fg'}{g^2}\) |
| 倒数法则 | \(\frac{1}{f}\) | \(\frac{-f'}{f^2}\) |
| 链式法则 | \(f 。g\) | \((f' 。g) g'\) |
链式法则一会儿我们会单独讲。
只要熟练运用这些法则和(王牌)公式,求导数的题就不成问题了。
复合函数
这也就是上一个表格中的最后一条:链式法则适用的范围。
考虑 \(f(g(x))\),这样的就叫复合函数。表示为 \(f。g\).注意是空心点,实心就成相乘了。
还要注意顺序。\(f(g(x)) \not = g(f(x))\),易知。因此求导时一定要注意不要搞反,否则全错!
导数应用
说一个非常常见的应用吧,比如求二次函数极值。
你只需要求出导数为 \(0\) 的那个点,然后判断是极小还是极大就行了。
比方说求 \(y=-5x^2+14x+3\) 的极值,其导数为 \(-10x+4\).
因此极值横坐标为 \(1.4\),坐标为 \((1.4,12.8)\),不难理解。
但是有的时候你会发现这不对,比方说:
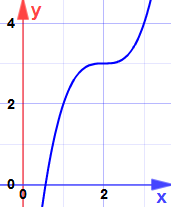
\(x=2\) 的时候导数可以为 \(0\),但是这?不对吧?
因此这也是“二次导数”的运用了。一会儿讲。
另外有个注意事项:函数一定要是可微分的,像 \(y=|x|\) 就不行,下面也有介绍!
二次导数
二次导数就是对导数再求导数。不多说。
运用就是在你求出导数为 \(0\) 要判断其是否为极值点时,应求此横坐标对应二次导数的值。为正,则极小。为 \(0\) 么,就是上图的情况了。
可微分
一个函数可以被微分的前提是其有导数。
考虑 \(y=|x|\) 在 \(x=0\) 时是否有导数?从左右两边趋近:
\(+\) 表示 \(x\) 为正,\(-\) 表示 \(x\) 为负。
你会发现两边趋近的答案不同,因此该点没有导数。
可以想象:对于任何一个函数,放大无穷倍后,会得到一条直线。
而 \(y=|x|\) 则仍然是折线。
但是我们可以定义一个范围使其可微分。比如:
\(f(x) = |x|\) 在域 \((0,\infty)\) 内可微分。(即 \(x>0\))
这才引入了我们的中心:微积分。
积分
积分入门
求积分和求导数是相反的过程。我们知道 \(\frac{d}{dx} x^2 = 2x\),因此 \(x^2\) 就是 \(2x\) 的积分!
这样子表示:
\(C\) 称为积分常数。原因很简单:形如 \(x^2+C\)(\(C\) 为常数)都可以是 \(2x\) 的积分。
我们需要更好的理解积分。一个小小的例子:
假设现在有一个无限大的水箱,有一个水龙头在注入水。则:
- 已知 \(x\) 时流速为 \(2x\),则 \(x\) 时水的总体积为?
- 已知 \(x\) 时水的总体积为 \(x^2\),则 \(x\) 时流速为?
但是这种题目对于一个新手似乎并不是特别容易。你可以做如下错误的尝试(对于第一问):
然后后面那个求和怎么求呢?根本求不出来吧。你硬说它是 \(\frac{n^2}{2}\) 未免太过偏见了。(平均为 \(\frac{n}{2}\)?)
其实可以用面积去理解: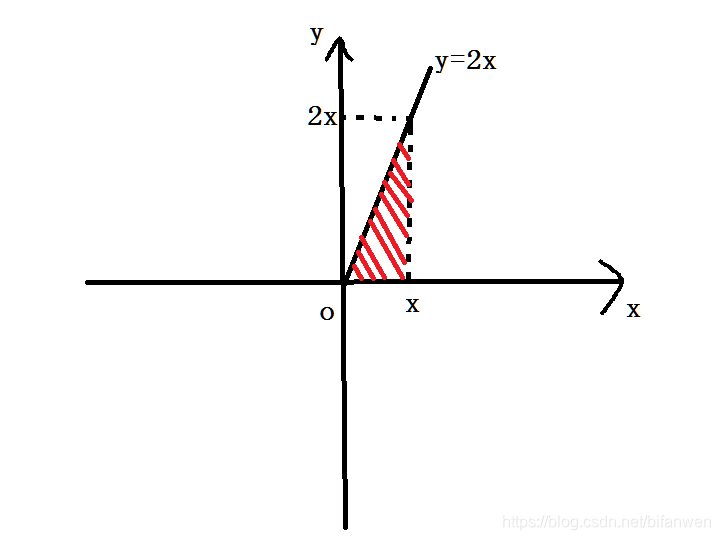
当然不是所有的面积都是这样简单,那样就是积分了。第二问也大概。一个求导一个积分,重点掌握。
求导数是很简单的。但有时求积分会非常困难,逆过来的过程就不那么容易。比方说你随便拿两个 \(10^{30}\) 级别的大素数相乘,然后让别人分解质因数一样。
因此,我们首先需要:
积分进阶
老规矩。
王牌公式:
| 常见函数 | 函数 | 积分 |
|---|---|---|
| 常数 | \(\int a \space dx\) | \(ax + C\) |
| 变量 | \(\int x \space dx\) | \(\frac{x^2}{2}+C\) |
| 平方 | \(\int x^2 \space dx\) | \(\frac{x^3}{3}+C\) |
| 指数 | \(\int x^n \space dx\) | \(\frac{x^{n+1}}{n+1}+C\) |
| 倒数 | \(\int \frac{1}{x} \space dx\) | \(\operatorname{In} \operatorname{abs}(x)+C\) |
| 指数 | \(\int e^x \space dx\) | \(e^x + C\) |
| 指数 | \(\int a^x \space dx\) | \(\frac{a^x}{\operatorname{In}(a)}+C\) |
| 指数 | \(\int \operatorname{In}(x) \space dx\) | \(x \operatorname{In} x - x + C\) |
| 三角函数 | \(\int \cos(x) \space dx\) | \(\sin(x)+C\) |
| 三角函数 | \(\int \sin(x) \space dx\) | \(-\cos(x)+C\) |
| 三角函数 | \(\int \sec^2(x) \space dx\) | \(\tan(x)+C\) |
积分法则:
| 法则 | 函数 | 积分 |
|---|---|---|
| 乘以常数 | \(\int cf(x) \space dx\) | \(c \int f(x) \space dx\) |
| 幂次数法则(\(n \not=-1\)) | \(\int x^n \space dx\) | \(\frac{x^{n+1}}{n+1}+C\) |
| 和(差)法则 | \(\int (f \pm g) \space dx\) | \(\int f \space dx \pm \int g \space dx\) |
积分再进阶
积分不是那么简单,于是我们再进阶。
现在我们补上两个法则:
乘法则
\(\int uv \space dx = u∫v \space dx −∫u' (∫v \space dx) \space dx\)
\(u'\) 表示 \(u\) 的积分。
注意选择 \(u,v\) 的时候一定要注意:
- \(u,v\) 的积分必须要好计算,否则会越来越复杂。
- \(u' (∫v \space dx)\) 是乘法,尽量是能消掉的那种,否则再次调用乘法则会繁琐(有时是不可避免的)。
定积分入门
积分用来表示曲线下方与 \(x\) 轴交出的面积 。而定积分指的就是确定区间 \([a,b]\) 的积分,表示为:
个人来讲,表示 \(x=a,x=b\),\(x\) 轴与 \(f(x)\) 上 \(x \in[a,b]\) 时 \(y\) 的曲线所构成。图:
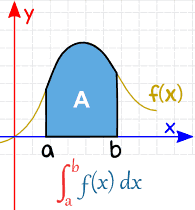
而不定积分其实也就是不确定的,比如:
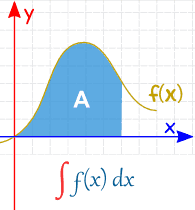
而定积分像是区间和,不定积分像是前缀和,因此可以计算定积分。比如 \(f(x)=2x\) 时:
\(\int_1^2 f(x) dx = (2^2+C) - (1^2+C) = 3\)
利用 \(2\) 点的积分减掉 \(1\) 点的积分即可。因此常数 \(C\) 通常不参与定积分运算。
再比如
这些也都还算基础。来道有点小坑的:
看起来是负数,但实际上 \(\cos(0) = 1\),因此
很小,但并非负数。
但也真的存在负数的情况,比方说搞到 \(x\) 轴下面:
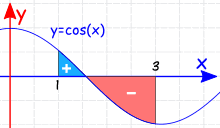
这也就是最基础的部分了。
好了,反正感觉高联上大学知识对于积分的要求也就这么多了吧。
如果以后上了大学可能会更。
\(\uparrow\) 扯。
微分方程
微分方程即存在至少 \(1\) 个导数的方程。
基础概念
-
阶数:即最高的导数阶数(一阶?二阶?)
-
次数:最高导数的指数。注意 “最高导数”,即使阶次低的导数指数更大我们也只计最高导数的指数。
-
常微分方程(ODE):只有一个自变量。
-
偏微分方程(PDE):有 \(\geq 2\) 个自变量。
比方说:
就是一个 三阶一次常微分方程。
- 线性微分方程:变量(和其导数)没有指数或与其他函数相乘的微分方程。即不会有 \(x \sin(x) , dx \log_{10} x\) 这种东西出现。
解一阶线性微分方程
标准形式:
一个小插曲。
是否记得解一元三次方程的时候,对于 \(x^3 + px + q = 0\),有这样一种解法:
就是把 \(x = u + v\) 代入,得到一个关于 \(u,v\) 的式子。
由于 \(u,v\) 还可以再满足一个条件(而这个条件是否满足是要看 \(\triangle\)),于是我们直接搞掉了一个系数。
然后方程解完。
所以我们是否也可以对微分方程进行类似的操作?
五步走。
-
设 \(y = uv\),由于导数法则,\(dy = u \space dv + v \space du\).
-
将含 \(v\) 的部分因式分解
-
设 \(v\) 的项为零,得到关于 \(u,x\) 的微分方程,并用分离变量法解 \(u\).
-
带回第二步得到一个方程,同样解 \(v\).
-
\(y=uv\) 即可。
举一个例子。
\(c\) 是一个常数,也就是说只要满足 \(y = x \operatorname{In}(cx)\) 的,都满足原方程,也就是其解。
然而有的时候分离常数法并不是那么靠谱。
求解微分方程
你还是按照上述方法一步步走,可以顺利地解出 \(u = \frac{e^{-x^2}}{k}\),\(k\) 为常数。
然后解 \(v\) 的时候,你发现你要解一个积分:
你就不得不动用积分的乘法则,然后你发现乘法则似乎特别适合这道题。
然后可以知道这个积分的结果是 \(ke^{x^2}(1-x^2) + D\),\(D\) 为常数。
然后你就能解出
一阶线性微分方程是不是很简单!!!