在一个差分约束系统中,线性规划矩阵A的每一行包括一个-1 和一个 1 ,其余所有项皆为0, 因此,由Ax <= b所给出的约束条件变为m个涉及n个变量的差额限制条件,其中的每个约束条件是一个简单的线性不等式:xj - xi <= bk;这里(1 <= i, j <= n, i != j, 1 <= k <= m);
例如我们考虑寻找满足下列条件的一个5维向量x = (xi)的问题:

这个问题与寻找满足下列的8个差分约束的变量x1, x2, x3, x4, x5的取值范围等价:
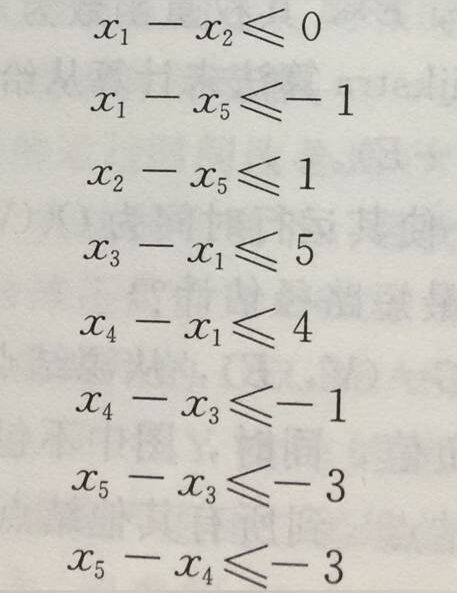
这个问题的答案是x = (-5, -3, 0, -1, -4)。
引理:设向量A = (x1, x2...xn)是差分约束系统Ax <= b的一个解,那么B = (x1 + d, x2 + d, ... xn + d)也是满足该约束系统的一个解。
给定差分约束系统Ax <= b,其对应的约束图是一个带权重的有向图G = (V, E),这里
V = {V0, V1 ... Vn}
E = {(vi, vj):xj - xi <= bk 是一个约束条件}U {(vo, v1), (v0, v2).....(v0, vn)};
图中包含一个额外的结点v0,用来保证图中至少存在一个结点,从其出发可以到达所有的目的地。
下面是上述不等式的图:
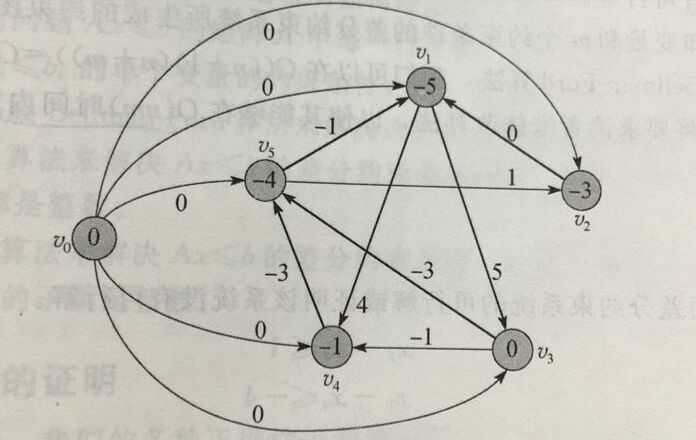
利用Bellman-Ford算法可以求解一个向量使得其满足约束条件,如果不存在解则函数返回false。
后续会跟进差分约束相关题目。