先插入代码
1 import numpy as np 2 import matplotlib.pyplot as plt 3 import pandas as pd 4 from sklearn.model_selection import train_test_split 5 from sklearn.linear_model import Lasso, Ridge 6 from sklearn.model_selection import GridSearchCV 7 8 9 if __name__ == "__main__": 10 # pandas读入 11 data = pd.read_csv('8.Advertising.csv') # TV、Radio、Newspaper、Sales 12 x = data[['TV', 'Radio', 'Newspaper']] 13 # x = data[['TV', 'Radio']] 14 y = data['Sales'] 15 print x 16 print y 17 18 x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=1) 19 # print x_train, y_train 20 model = Lasso() 21 # model = Ridge() 22 23 alpha_can = np.logspace(-3, 2, 10) 24 lasso_model = GridSearchCV(model, param_grid={'alpha': alpha_can}, cv=5) 25 lasso_model.fit(x_train, y_train) 26 print '验证参数: ', lasso_model.best_params_ 27 28 y_hat = lasso_model.predict(np.array(x_test)) 29 mse = np.average((y_hat - np.array(y_test)) ** 2) # Mean Squared Error 30 rmse = np.sqrt(mse) # Root Mean Squared Error 31 print mse, rmse 32 33 t = np.arange(len(x_test)) 34 plt.plot(t, y_test, 'r-', linewidth=2, label='Test') 35 plt.plot(t, y_hat, 'g-', linewidth=2, label='Predict') 36 plt.legend(loc='upper right') 37 plt.grid() 38 plt.show()
代码解析(以行号为基准)
11行:读取csv数据,n行4列,(4列分别为TV、Radio、Newspaper、Sales)
12行:选取(TV、Radio、Newspaper)这三个数据为特征量,
14行:sales为对应的数值(公式:y(sales) =θ0x0 + θ1x(tv) + θ2x(radio) + θ3x(np))
18行:对x,y随机做采样,一部分做测试数据,一部分做训练数据,random_state=1是为了确保每次的数据都一致
20行:lasso 又称 L1正则化,通过最小二乘法去计算满足J(θ)最小的条件的θ的值,(Ridge又称L2正则化)
线性回归 --》最大似然估计 --》 最小二乘法的推理( )
)

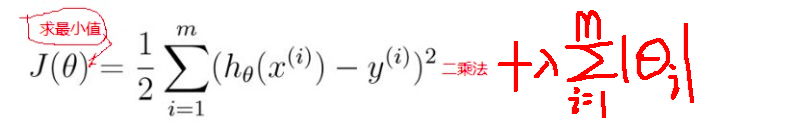
Lasso(), 或Ridge() 是为了防止过拟合的有效操作
23,24行:利用交叉验证寻找最优的alpha_can值
25行:lasso_model.fit(x_train, y_train)利用训练数据进行学习
28行:y_hat是x_test的一个预测值,x_text的实际值是y_text,lasso_model.predict()是我们学好了的一个模型
29行:以均方误差作为一个度量值
30行:将均方误差进行开根号
线性回归数学原理解析:
注:具体的数学推导公式就不写了上面的博客有,另外实际中勘用的模型和数学中严禁的思维逻辑要有差别。
其次,如要错误请无情指出。。。博主的求生欲还是很强哒。
正文:
首先以一元的线性回归为例 Y = θ0Xo + θ1X1 其实Y可以看做 两个向量相乘的结果 θ=(θ0, θ1 ......) 和 X=(X0, X1 ......) ----> Y = θT.X,在实际预测中 y_hat 总会存在与实际值的误差ε,当数据 足够大是 ε会服从高斯分布,我们假设ε是独立的 满足其概率密度函数的条件,此时 因为x,和y是样本数据所以是已知的,那此时我们只需要满足条件的参数的θ的值。
我们 假定样本是独立分布的,则样本的联合概率是各自边缘概率的乘积得出:
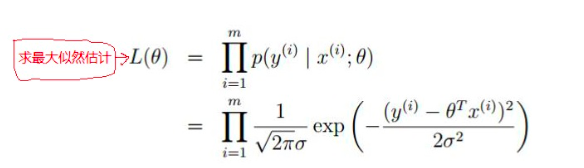
对L(θ)取对数得到最小二乘法的损失函数J(θ)
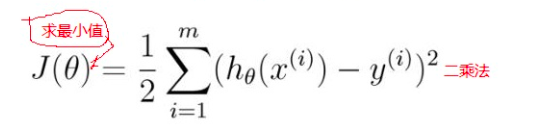
线性模型评价指标
均方误差: sklearn.metrics.mean.squared_error(y, pred_y),
均方误差是反应 真实值和预测值直接误差的一种度量,既然是误差那当然是越小越好,均方误差是指参数估计值与参数真值之差平方的期望值; MSE可以评价数据的变化程度,MSE的值越小,说明预测模型描述实验数据具有更好的精确度。

平均绝对值误差:sklearn.metrics.mean_absolute_error(y, pred_y)
平均绝对误差能更好地反映预测值误差的实际情况.

中值绝对误差:sklearn.metrics.median_absolute_error(y, pred_y)
中值绝对误差,先计算出数据与中位数之间的偏差,然后获得所有偏差中的中位数
R2 决定系数(拟合优度)sklearn.metrics.r2_score(y, pred_y)
得分越接近1 说明拟合程度越好,