题目描述
经过千辛万苦小 A 得到了一块切糕,切糕的形状是长方体,小 A 打算拦腰将切糕切成两半分给小 B。出于美观考虑,小 A 希望切面能尽量光滑且和谐。于是她找到你,希望你能帮她找出最好的切割方案。
出于简便考虑,我们将切糕视作一个长 P、宽 Q、高 R 的长方体点阵。我们将位于第 z层中第 x 行、第 y 列上(1≤x≤P, 1≤y≤Q, 1≤z≤R)的点称为(x,y,z),它有一个非负的不和谐值 v(x,y,z)。一个合法的切面满足以下两个条件:
与每个纵轴(一共有 P*Q 个纵轴)有且仅有一个交点。即切面是一个函数 f(x,y),对于所有 1≤x≤P, 1≤y≤Q,我们需指定一个切割点 f(x,y),且 1≤f(x,y)≤R。
切面需要满足一定的光滑性要求,即相邻纵轴上的切割点不能相距太远。对于所有的 1≤x,x’≤P 和 1≤y,y’≤Q,若|x-x’|+|y-y’|=1,则|f(x,y)-f(x’,y’)| ≤D,其中 D 是给定的一个非负整数。 可能有许多切面f 满足上面的条件,小A 希望找出总的切割点上的不和谐值最小的那个。
输入输出格式
输入格式:
第一行是三个正整数P,Q,R,表示切糕的长P、 宽Q、高R。第二行有一个非负整数D,表示光滑性要求。接下来是R个P行Q列的矩阵,第z个 矩阵的第x行第y列是v(x,y,z) (1<=x<=P, 1<=y<=Q, 1<=z<=R)。 100%的数据满足P,Q,R<=40,0<=D<=R,且给出的所有的不和谐值不超过1000。
输出格式:
仅包含一个整数,表示在合法基础上最小的总不和谐值。
输入输出样例
输入样例#1:
2 2 2
1
6 1
6 1
2 6
2 6
输出样例#1:
6
题解
题目要求就是在一个(n imes m)的矩阵中填数
每个位置都是一个数轴,数轴上每一格都代表了一个数,相邻两点间所选择的数轴上的位置的距离不超过(D)
,问将矩阵填成(n imes m)的最小花费
可以发现每个点的贡献最多只能被计算一次
那么可以用最小割来解决
用(v_{i,j,k})表示第(i)行,第(j)列,数轴上选择第(k)个点的值
我们可以把每个位置上的数轴的相邻点(v_{i,j,k-1} o v_{i,j,k})之间连边,流量就是(v_{i,j,k})
这样如果选择了数轴上的第(k)个点就要割掉这条边并花费(v_{i,j,k})
然后我们还需要考虑一个限制就是相邻的点在数轴上选择的距离不超过(D)
那么我们对于点((i,j)),只需满足(f(i,j)-f(x,y)le d)即可
因为如果(f(i,j) - f(x,y) < -d)
那么在点((x,y))的限制中就成了(f(x,y)-f(i,j) > d)
那么这显然不满足条件
所以只连((i,j,k) o (i,j,k-d))的边,流量为(INF),表示这条限制不会被割掉
有一位(dalao)的图画的肥肠形象
盗用一下以便理解==
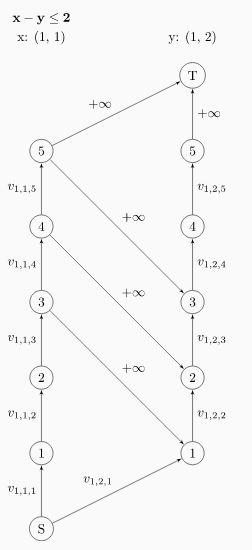
代码
/*
对于光滑的限制:
只需要考虑f(i,j) - f(x,y) <= d 即可
因为如果存在 f(i,j) - f(x,y) < -d
那么换做f(x,y)的限制就成了f(x,y) - f(i.j) > d
也自然就不符合条件了
*/
#include<queue>
#include<cstdio>
#include<cstring>
#include<algorithm>
const int N = 45 ;
const int M = 100005 ;
const int INF = 1e9 ;
const int dx[] = {-1 , 0 , 1 , 0} ;
const int dy[] = {0 , -1 , 0 , 1} ;
using namespace std ;
inline int read() {
char c = getchar() ; int x = 0 , w = 1 ;
while(c>'9'||c<'0') { if(c=='-') w = -1 ; c = getchar() ; }
while(c>='0'&&c<='9') { x = x*10+c-'0' ; c = getchar() ; }
return x*w ;
}
int n , m , h , d , S , T , cnt , num = 1 ;
int id[N][N][N] , val[N][N][N] , hea[M] , dep[M] ;
struct E { int nxt , to , dis ; } edge[M * 10] ;
inline void Insert_edge(int from , int to , int dis) {
edge[++num].nxt = hea[from] ; edge[num].to = to ;
edge[num].dis = dis ; hea[from] = num ;
}
inline void add_edge(int u , int v , int w) {
Insert_edge(u , v , w) ;
Insert_edge(v , u , 0) ;
}
inline bool bfs() {
queue < int > q ; q.push(S) ;
memset(dep , 0 , sizeof(dep)) ; dep[S] = 1 ;
while(!q.empty()) {
int u = q.front() ; q.pop() ;
for(int i = hea[u] ; i ; i = edge[i].nxt) {
int v = edge[i].to ;
if(!dep[v] && edge[i].dis > 0) {
dep[v] = dep[u] + 1 ;
q.push(v) ;
}
}
}
return dep[T] ;
}
int dfs(int u , int dis) {
if(u == T || !dis) return dis ;
int sum = 0 ;
for(int i = hea[u] ; i ; i = edge[i].nxt) {
int v = edge[i].to ;
if(dep[v] == dep[u] + 1 && edge[i].dis > 0) {
int diss = dfs(v , min(dis , edge[i].dis)) ;
if(diss > 0) {
edge[i].dis -= diss ; edge[i ^ 1].dis += diss ;
sum += diss ; dis -= diss ; if(!dis) break ;
}
}
}
if(!sum) dep[u] = -1 ; return sum ;
}
inline int dinic() {
int ans = 0 ;
while(bfs())
ans += dfs(S , INF) ;
return ans ;
}
int main() {
n = read() ; m = read() ; h = read() ; d = read() ;
S = 0 ; T = n * m * h + 1 ;
for(int k = 1 ; k <= h ; k ++)
for(int i = 1 ; i <= n ; i ++)
for(int j = 1 ; j <= m ; j ++) {
id[i][j][k] = ++ cnt ;
val[i][j][k] = read() ;
}
for(int i = 1 ; i <= n ; i ++)
for(int j = 1 ; j <= m ; j ++) {
for(int k = 1 ; k <= h ; k ++)
add_edge(id[i][j][k - 1] , id[i][j][k] , val[i][j][k]) ;
add_edge(id[i][j][h] , T , INF) ;
}
for(int i = 1 ; i <= n ; i ++)
for(int j = 1 ; j <= m ; j ++)
for(int k = d + 1 ; k <= h ; k ++)
for(int t = 0 , x , y ; t < 4 ; t ++) {
x = i + dx[t] , y = j + dy[t] ;
if(x < 1 || y < 1 || x > n || y > m) continue ;
add_edge(id[i][j][k] , id[x][y][k - d] , INF) ;
}
printf("%d
",dinic()) ;
return 0 ;
}