§4-2 方差
一.方差的概念
1、定义4.3:设 随机变量X的数学期望为E(X),若E(X-E(X))2存在,则称它为X的方差(此时,也称X的方差存在),记为D(X)或Var(X),即
随机变量X的数学期望为E(X),若E(X-E(X))2存在,则称它为X的方差(此时,也称X的方差存在),记为D(X)或Var(X),即
D(X)=E(X-E(X))2
称D(X)的算术平方根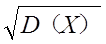 为X的标准差或均方差,记为
为X的标准差或均方差,记为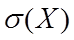 ,即
,即
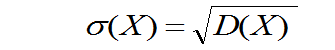
由数学期望的性质5知,若随机变量X的方差D(X)存在,则D(X)³0。简言之,方差是一个非负实数。
当X服从某分布时,我们也称某分布的方差为D(X)。
2、计算方差
(1)若X是离散型随机变量,其分布律为pi=P(X=xi),i=1,2,...,且D(X)存在,则
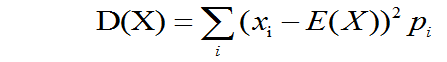
(2)若X是连续型随机变量,其概率密度为f(x),且D(X)存在,则
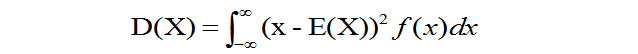
(第一版)
例1:设X~B(1,p),求D(X)
例2:设X~N(m,s2),求D(X)
例3:设X~U[a,b],求D(X)
(3)D(X)=E(X2)-(EX)2
证明:P112.
- P112
- P112
(第一版)
例4:设X~p(l),求D(X)
例5:已知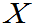
 ,求
,求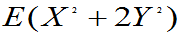
二.方差的性质
性质1:若C为常数,则
D(C)=0
性质2:若C为常数,随机变量X的方差存在,则CX的方差存在,且
D(CX)=C2D(X)
证明由自己完成
性质3:若随机变量X,Y相互独立,它们的方差都存在,则X±Y的方差也存在,且
D(X±Y)=D(X)+D(Y)
证明:P113
推论:若随机变量X1,X2,…,Xn相互独立,它们的方差都存在,则X1+X2+...+Xn的方差存在,且

性质4:若随机变量X的方差存在,对任意的常数C¹E(X),则
D(X)= <E(X-C)2
<E(X-C)2
即函数g(C)=E(X-C)2在C=E(X)处达到最小值D(X)。
性质5若D(X)存在,则D(X)=0的充要条件是:
P(X=E(X))=1
例3 P113
第一版例:
例6:X服从 B(n,p),求D(X).
例7:某种商品每件表面上的疵点数X服从泊松分布,平均每件上有0.8个疵点。若规定表面不超过一个疵点的为一等品,价值十元,表面疵点数大于1不多于4的为二等品,价值8元。某件表面疵点数是4个以上着为废品,求产品价值的均值和方差。
已知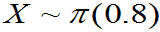
设产品价值为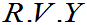
|
|
0 |
8 |
10 |
|
X |
(X>4) |
( |
(X |
|
P( |
P(X>4= 1-0.8088 -0.1898 |
P( =P( P( =[1-P( -[1-P( =0.1898 |
P(X =1- P(X =0.8088 |
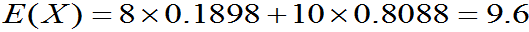 元
元


例 :设随机变量X的方差D(X)存在,且D(X)>0令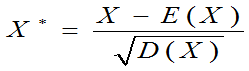 ,其中E(X)是X的数学期望,求
,其中E(X)是X的数学期望,求 。
。
三.契比雪夫不等式(Chebyshev)
契比雪夫不等式:设随机变量X的方差D(X)存在,则对任意的e>0,均有
P{êX-E(X)ï³e} £
或等价地
P{êX-E(X)ï<e}³1-
例:P{êX-E(X)ï<3σ}³0.8889
P{êX-E(X)ï<4σ}³0.9375
解:P{êX-E(X)ï<3σ}³1-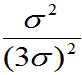
=1-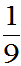
P{êX-E(X)ï<4σ}³1-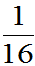
Data;
A=8/9; put a=;
A=15/16; put a=;
Run;
A=0.8888888889
A=0.9375
§4.3 几种生要随机变量的数学期望与方差
P115
这部分结果很重要,要牢记。
P117, 关于正态随机变量的三个重要数据:
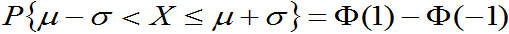
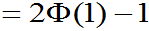
=0.6826894921
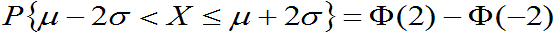
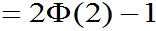
=0.9544997361
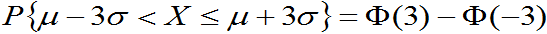
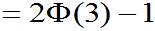
=0.9973002039
SAS的两种计算公式:
data;
p1=PROBNORM(1)-PROBNORM(-1); put p1=;
p2= PROBNORM(2)-PROBNORM(-2); put p2=;
p3= PROBNORM(3)-PROBNORM(-3); put p3=;
run;
p1=0.6826894921
p2=0.9544997361
p3=0.9973002039
data;
p1=2*PROBNORM(1)-1; put p1=;
p2=2*PROBNORM(2)-1; put p2=;
p3=2*PROBNORM(3)-1; put p3=;
run;
p1=0.6826894921
p2=0.9544997361
p3=0.9973002039
也可以验证数据,即以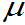 为中心,需要几倍的标准差
为中心,需要几倍的标准差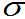 距离所构成的区间,其区间内的概率为上述所示。
距离所构成的区间,其区间内的概率为上述所示。
Data;
q1=abs(probit((1-0.6826894921)/2));put q1=;
q2=abs(probit((1-0.9544997361)/2));put q2=;
q3=abs(probit((1-0.9973002039)/2));put q3=;
run;
q1=0.9999999999
q2=2
q3=2.9999999959
data;
q1=probit(1-(1-0.6826894921)/2);put q1=;
q2=probit(1-(1-0.9544997361)/2);put q2=;
q3=probit(1-(1-0.9973002039)/2);put q3=;
run;
q1=0.9999999999
q2=2
q3=2.9999999959
注意: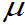 为中心,概率为90%,95%,98%,99%的区间,需要几倍的标准差
为中心,概率为90%,95%,98%,99%的区间,需要几倍的标准差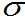 距离。
距离。
Data;
q1=abs(probit((1-0.9)/2));put q1=;
q2=abs(probit((1-0.95)/2));put q2=;
q3=abs(probit((1-0.98)/2));put q3=;
q3=abs(probit((1-0.99)/2));put q3=;
run;
q1=1.644853627
q2=1.9599639845
q3=2.326347874
q3=2.5758293035
比如,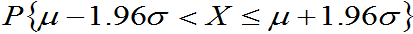
=0.95
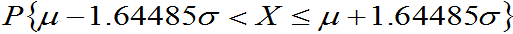
=0.9
等的结论也是常用的。几乎都成常识了。
书示附表1中列出了多种常用的随机变量的数据期望和方差。

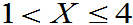 )
)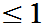 )
) Y=k)
Y=k) )
) 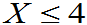 )-
)- 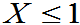 )
) 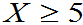 )]
)] 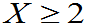 )]
)]  )
)  )
) 