第十讲 矩阵的三角分解
一、 Gauss消元法的矩阵形式
n元线性方程组
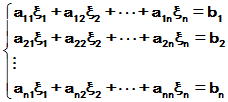

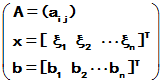
设 ,设A的k阶顺序主子式为
,设A的k阶顺序主子式为 ,若
,若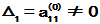 ,可以令
,可以令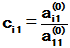
并构造Frobenius矩阵

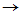
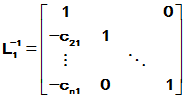
计算可得

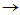
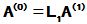
该初等变换不改变行列式,故 ,若
,若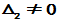 ,则
,则 ,又可定义
,又可定义
 ,并构造Frobenius矩阵
,并构造Frobenius矩阵

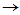
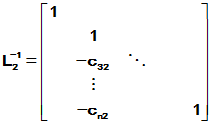
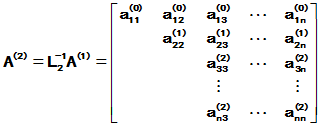
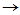
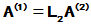
依此类推,进行到第(r-1)步,则可得到
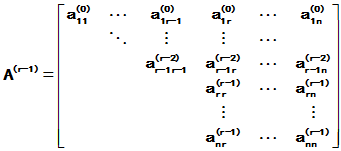 (r=2,3,
(r=2,3,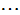 ,n-1)
,n-1)
则A的r阶顺序主子式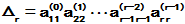 ,若
,若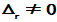 ,则
,则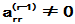 可定义
可定义 ,并构造Frobenius矩阵
,并构造Frobenius矩阵
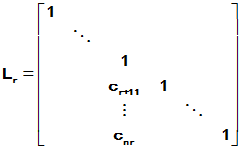
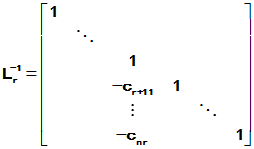

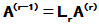
(r=2,3, ,n-1)
,n-1)
直到第(n-1)步,得到
 则完成了消元的过程
则完成了消元的过程
而消元法能进行下去的条件是 (r=1,2,
(r=1,2, ,n-1)
,n-1)
二、 LU分解与LDU分解
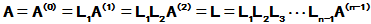
容易求出
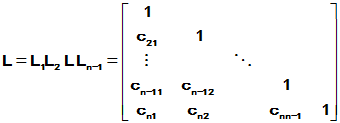 为下三角矩阵
为下三角矩阵
令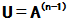 为上三角矩阵,则
为上三角矩阵,则
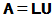 (L: lower U: upper L: left R: right)
(L: lower U: upper L: left R: right)
以上将A分解成一个单位下三角矩阵与上三角矩阵的乘积,就称为LU分解或LR分解。

 两个三角方程回代即可
两个三角方程回代即可
LU分解不唯一,显然,令D为对角元素不为零的n阶对角阵,则
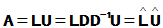
可以采用如下的方法将分解完全确定,即要求
- L为单位下三角矩阵
- U为单位上三角矩阵
- 将A分解为LDU,其中L、U分别为单位下三角、单位上三角矩
阵,D为对角阵D=diag[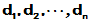 ],而
],而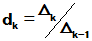 (k=1,2,…n),
(k=1,2,…n),
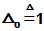 。
。
n阶非奇异矩阵A有三角分解LU或LDU的冲要条件是A的顺序主子式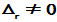 (r=1,2,
(r=1,2,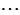 ,n)
,n)
n个顺序主子式全不为零的条件实际上是比较严格的,特别是在数值计算中,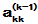 很小时可能会带来大的计算误差。因此,有必要采取选主元的消元方法,这可以是列主元(在
很小时可能会带来大的计算误差。因此,有必要采取选主元的消元方法,这可以是列主元(在 ,
,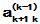 ,…
,…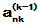 中选取模最大者作为新的
中选取模最大者作为新的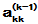 )、行主元(在
)、行主元(在 ,
,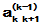 ,…
,…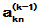 中选取模最大者作为新的
中选取模最大者作为新的 )全主元(在所有
)全主元(在所有 (
( )中选模最大者作为新的
)中选模最大者作为新的 )。之所以这样做,其理论基础在于对于任何可逆矩阵A,存在置换矩阵P使得PA的所有顺序主子式全不为零。
)。之所以这样做,其理论基础在于对于任何可逆矩阵A,存在置换矩阵P使得PA的所有顺序主子式全不为零。
列主元素法:在矩阵的某列中选取模值最大者作为新的对角元素,选取范围为对角线元素以下的各元素。比如第一步:找第一个未知数前的系数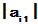 最大的一个,将其所在的方程作为第一个方程,即交换矩阵的两行,自由项也相应变换;第二步变换时,找
最大的一个,将其所在的方程作为第一个方程,即交换矩阵的两行,自由项也相应变换;第二步变换时,找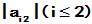 中最大的一个,然后按照第一步的方法继续。
中最大的一个,然后按照第一步的方法继续。
行主元素法:在矩阵的某行中选取模值最大者作为新的对角元素,选取范围为对角线元素以后的各元素,需要记住未知数变换的顺序,最后再还原回去。因此需要更多的存储空间,不如列主元素法方便。
全主元素法:若某列元素均较小或某行元素均较小时,可在各行各列中选取模值最大者最为对角元素。与以上两种方法相比,其计算稳定性更好,精度更高,计算量增大。
三、其他三角分解
1. 定义 设A具有唯一的LDU分解
- 若将D、U结合起来得
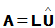 (
(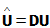 ),则称为A的Doolittle分解
),则称为A的Doolittle分解
- 若将L、D结合起来得
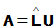 (
(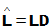 ),则称为A的Crout分解
),则称为A的Crout分解
2. 算法
- Crout分解,设
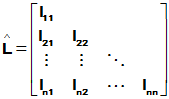 ,
,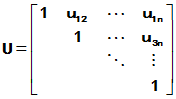
由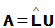 乘出得
乘出得
① 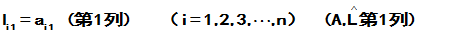
② 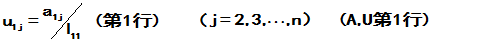
③ 
④ 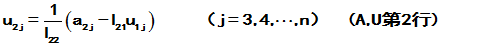
⑤ 一般地,对A,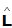 的第k列运算,有
的第k列运算,有
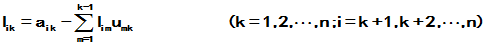
⑥ 对A,U的第k行运算,有
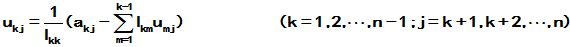
直至最后,得到的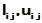 恰可排成
恰可排成
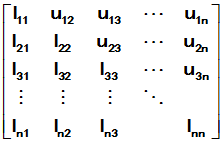 先算列后算行
先算列后算行
3. 厄米正定矩阵的LU分解(Cholesky分解)
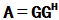
其中G为下三角矩阵,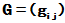
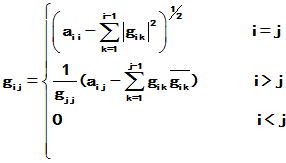
理论上,Cholesky具有中间量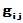 可以控制(
可以控制(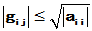 )的好处,应较稳健,但实际计算中发现,对希尔伯特矩阵问题,不如全主元方法。
)的好处,应较稳健,但实际计算中发现,对希尔伯特矩阵问题,不如全主元方法。
作业:p195 2、3
