Heap

Heap is a special case of balanced binary tree data structure where the root-node key is compared with its children and arranged accordingly.
If 'a' has child node 'b' then -
key(a) >= key(b)
As the value of parent is greater than that of child, this property generates Max Heap.
Based on the criteria, a heap can be of two types -

For Input -> 35 33 42 10 44 19 27 44 26 31
Min-Heap - Where the value of the root node is less than or equal to either of its children.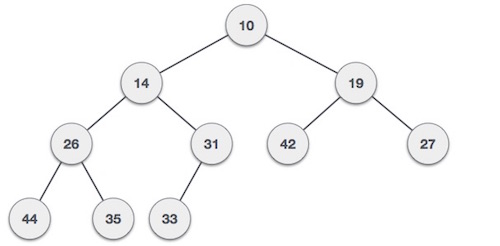

Max-Heap - Where the value of the root node is greater than or equal to either of its children.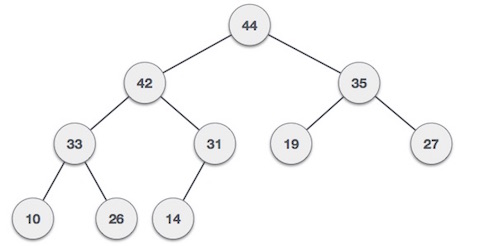

Max Heap Construction
We shall use the same example to demonstrate how a Max Heap is created.
The procedure to create Min Heap is similar but we go for min values instead of max values.

We are going to derive an algorithm for max heap by inserting one element at a time.
At any point of time, heap must maintain its property. while insertion, we also assume that we are inserting a node in an already heapified tree.

Step 1 - Create a new node at the end of heap and assign new value to the node.
Step 2 - Compare the value of this child node with its parent.
Step 3 - If value of parent is less than child, then swap them.
Step 4 - Repeat step 2 & 3 until Heap property holds.

Note - In Min Heap construction algorithm, we expect the value of the parent node to be less than that of the child node.

Let's understand Max Heap construction by an animated illustration.
We consider the same input sample that we used earlier.

Max Heap Deletion Algorithm

Let us derive an algorithm to delete from max heap.
Deletion in Max (or Min) Heap always happens at the root to remove the Maximum ( or minimum) value.

Step 1 - Remove root node.
Step 2 - Move the last element of last level to root.
Step 3 - Compare the value of the child node with its parent
Step 4 - If value of parent is less than child, then swap them(swap with the max of the left child and the right child)
Step 5 - Repeat step 3 & 4 until Heap property holds.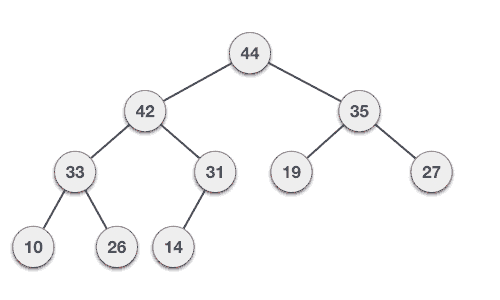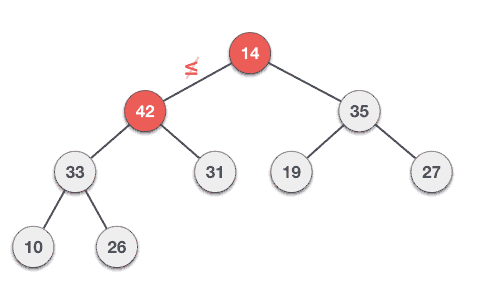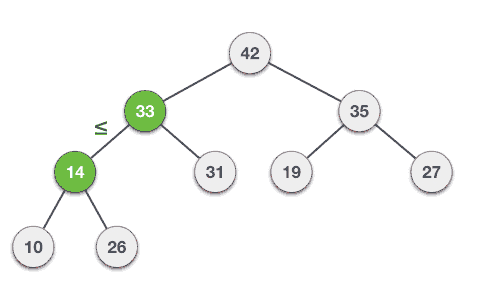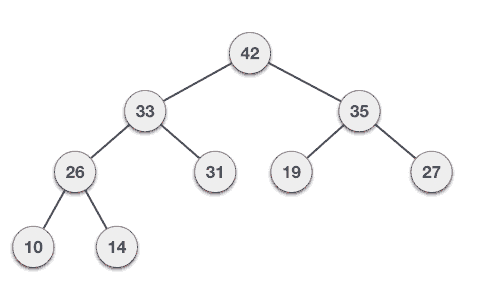

Heap Sort

堆排序，通常来说堆排序是以数组来存储堆结构的。

比如一个有n个节点的heap, 其存储数组 heap[n+1]， heap[0]不使用，使用 heap[1]到 heap[n] 这些数组元素。

这样做是为了对应堆中数据从下标1开始，经过这样处理，一个节点 (下标为 i )的：

.父节点的下标为 i / 2 i = 1，2， ... n

.左孩子下标为 i * 2

.右孩子下标为 i * 2 + 1

排序的过程:

1. 对于一个最大堆，其根节点(就是数组的第[1]个，即heap[1]，不是heap[0], [0]从不使用）是整个堆中最大节点，将它和最后一个节点交换

这样最大的节点就放在数组的最后一个。

2. 将去掉(不是真正的去掉,只是它不再参与排序了，因为它是最大的)最后一个元素的数组，视作一个新的Max-Heap，然后按Max-Heap的要求，将剩下的 heap[1] 到 heap[n-1] 之间的所有节点，

重新转换成Max-Heap（和上面的删除节点的算法一样), 这样剩下的仍是一个Max-Heap.

3. 重复 1 & 2，这样每次将最大根节点(也就是heap[1])移到新Max-Heap的最后一个。

直到只剩下heap[1],heap[2], 此时这个两个节点仍是一个最大堆，也就是说， heap[1] > heap[2] (为什么这么肯定？因为Max-Heap就这特性，父结点就大于子结点)

此时只要交换heap[1],heap[2]即可，这也是递归结束的条件。

简单点说，每次把heap[1]和数组最后一个交换。交换后不管最后那个元素，将最后元素之前的所有元素再视作一个新的，但要重新处理的堆。

处理后，就变成比最开始的堆少一个元素的新Max-Heap。然后再把heap[1]和新的Max-Heap的最后一个换，然后再处理成新的Max-Heap,

再换，再处理，...

最后原数组变为一个升序的数组.

其实图片最直观，懒得画了。

Golang:

package binary_search_tree

import (
    "fmt"
)

type Heap struct {
    Data     []int
    Size     int
    Capacity int
}

func CreateEmptyMaxHeap(capacity int) *Heap {
    heap := &Heap{Size: 0, Capacity: capacity}
    heap.Data = make([]int, capacity+1) // Data[0] not used.
    return heap
}

// i is array index, from 0
func (h *Heap) swap(i int) {
    if i == 1 { // root
        return
    }
    parent := i / 2
    if h.Data[i] > h.Data[parent] {
        h.Data[i], h.Data[parent] = h.Data[parent], h.Data[i]
    } else {
        return
    }
    h.swap(parent)
}

// swap with the max of the left child and the right child
func (h *Heap) swap2(i int) {
    lefti := i * 2
    righti := i*2 + 1

    // get max of left and right
    max := 0
    if lefti <= h.Size {
        max = lefti
    }
    if righti <= h.Size && h.Data[righti] > h.Data[lefti] {
        max = righti
    }

    if h.Data[i] < h.Data[max] {
        h.Data[i], h.Data[max] = h.Data[max], h.Data[i]
        h.swap2(max)
    }
}

func (h *Heap) Insert(data int) {
    h.Size = h.Size + 1
    i := h.Size
    h.Data[i] = data
    h.swap(i)
}

// delete root node, i.e. Data[1]
func (h *Heap) Delete() {
    h.Data[1], h.Data[h.Size] = h.Data[h.Size], h.Data[1]
    h.Print()
    h.Size = h.Size - 1
    h.swap2(1)
}

func (h *Heap) Sort() {
    size := h.Size
    for i := h.Size; i >= 2; i-- {
        h.Data[1], h.Data[h.Size] = h.Data[h.Size], h.Data[1]
        h.Size = h.Size - 1
        if i == 2 {
            break
        }
        h.swap2(1)
        h.Print()
    }
    h.Size = size
}

func (h *Heap) Print() {
    for i := 1; i <= h.Size; i++ {
        fmt.Printf(" %d", h.Data[i])
    }
    fmt.Println("")
}

test:

package main

import (
    bst "binary_search_tree"
)

func testMaxHeap() {
    data1 := []int{35, 33, 42, 10, 14, 19, 27, 44, 26, 31}
    heap1 := bst.CreateEmptyMaxHeap(20)
    for i := 0; i < len(data1); i++ {
        heap1.Insert(data1[i])
    }
    heap1.Print()
    heap1.Sort()
    heap1.Print()
}

func main() {
    testMaxHeap()
}

output:

 44 42 35 33 31 19 27 10 26 14
 42 33 35 26 31 19 27 10 14
 35 33 27 26 31 19 14 10
 33 31 27 26 10 19 14
 31 26 27 14 10 19
 27 26 19 14 10
 26 14 19 10
 19 14 10
 14 10
 10 14 19 26 27 31 33 35 42 44