自己开发了一个股票智能分析软件,功能很强大,需要的点击下面的链接获取:
https://www.cnblogs.com/bclshuai/p/11380657.html
1.1 偏差方差分解
拟合能力强的模型复杂度比较高,但是容易导致过拟合,泛化能力差。如果降低模型的复杂度,降低拟合能力,又会导致欠拟合。所以需要在过拟合和欠拟合之间找到一个平衡。这个很好理解,以多项式拟合为例,多项式的阶数越高,拟合的误差越小,但是如果用于计算拟合数据以外的数据,就会出现很大的偏差,泛化能力差。如果阶数越小,泛化能力很强。
在实际训练中,通过采样样本集进行训练,不同的样本集D上训练得到不同的模型参数fD(x)。有个最优的模型参数,使得平方损失函数最小的模型f*(x)。
偏差:指样本训练值平均值与最优模型值之间的差距;衡量模型的拟合能力。
方差:指的是一个模型在多个训练样本集上的差异,反映为多个样本训练值之间的集中程度;如果越集中则方差越小。泛化能力越强,能够适应不同的样本集。
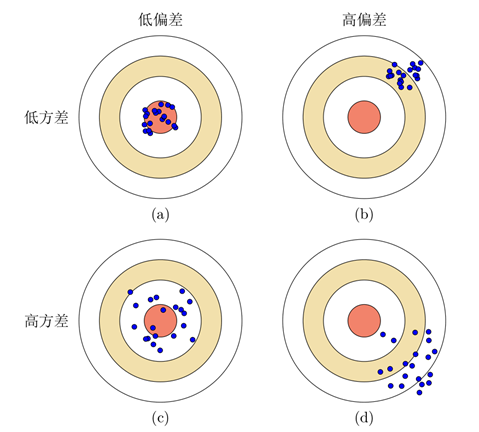
复杂度高的模型拟合能力强,容易过拟合,在训练集上偏差小,但是在验证集上偏差大。我们需要通过降低模型复杂度来增强泛化能力,使其在验证集上的偏差也能减小。如果模型在训练集上的偏差比较大,说明模型欠拟合,可以通过增加复杂度来提高拟合能力,减小偏差。以结构风险最小化为例,我们可以增大正则化系数降低模型的复杂度,增强泛化能力,减小过拟合引起的偏差.也可以减小正则化系数,提高拟合能力.因此,一个好的正则化系数需要在偏差和方差之间取得比较好的平衡.下图给出了机器学习模型的期望错误、偏差和方差随复杂度的变化情况,其中红色虚线表示最优模型.最优模型并不一定是偏差曲线和方差曲线的交点。
