其实问题就是给定y方向的视域角(alpha),和视域的宽高比(r),求投影矩阵。
我们首先假设投影平面距离摄像机的距离为(d),视域的宽为(w),高为(h),近剪裁面距离摄像机的距离为(n),远剪裁面距离摄像机的距离为(f),那么首先有:
[r= frac{w}{h}
]
[tanfrac{alpha}{2} = frac{h}{d}
]
假设观察坐标系中的任一点(P),坐标为((x,y,z)),通过投影变换到投影平面的坐标为((x',y',z')),由相似三角形,得到:
[dfrac{x'}{x} = dfrac{d}{z}
]
[dfrac{y'}{y} = dfrac{d}{z}
]
综合上式,求出(x')和(y'):
[x'= dfrac{h x}{tandfrac{alpha}{2} z}
]
[y'= dfrac{h y}{tandfrac{alpha}{2} z}
]
位于视锥体中的(x')和(y')满足(-w leq x' leq w),(-h leq y' leq h),那么将其归一化有:
[x'= dfrac{x}{r tandfrac{alpha}{2} z}
]
[y'= dfrac{y}{tandfrac{alpha}{2} z}
]
注意到上述求得的(x')和(y')里的分母中均包含(z),为了用矩阵形式来表达投影变换,必须要借助齐次坐标,有:
[[x, y, z, 1] cdot egin{bmatrix} dfrac{1}{rtandfrac{alpha}{2}} & 0 & 0 & 0 \ 0 & dfrac{1}{tandfrac{alpha}{2}} & 0 & 0 \ 0 & 0 & A & 1 \ 0 & 0 & B & 0 end{bmatrix} = [x'cdot z, y' cdot z, Az+B, z]
]
因而可得到(z'=dfrac{Az+B}{z})。同时,我们希望(z')满足:
- (0 leq z' leq 1)
- 对于原始的(z_1,z_2),如果满足(z_1 < z_2),那么(z'_1 < z'_2)
因为原始的(z)范围为(n leq z leq f),所以有:
[egin{cases}
dfrac{An+B}{n} = 0 \
dfrac{Af+B}{f} = 1
end{cases}
]
解方程组,得到:
[egin{cases}
A = dfrac{f}{f - n} \
B = dfrac{nf}{n - f}
end{cases}
]
综上,得到最终的投影矩阵为
[egin{bmatrix} dfrac{1}{rtandfrac{alpha}{2}} & 0 & 0 & 0 \ 0 & dfrac{1}{tandfrac{alpha}{2}} & 0 & 0 \ 0 & 0 & dfrac{f}{f - n} & 1 \ 0 & 0 & dfrac{nf}{n - f} & 0 end{bmatrix}
]
所以,投影变换后的(z' = dfrac{f}{f - n} + dfrac{nf}{(n - f)z})。
让我们观察下不同情况下(n)和(f)的取值变换(z')的函数曲线。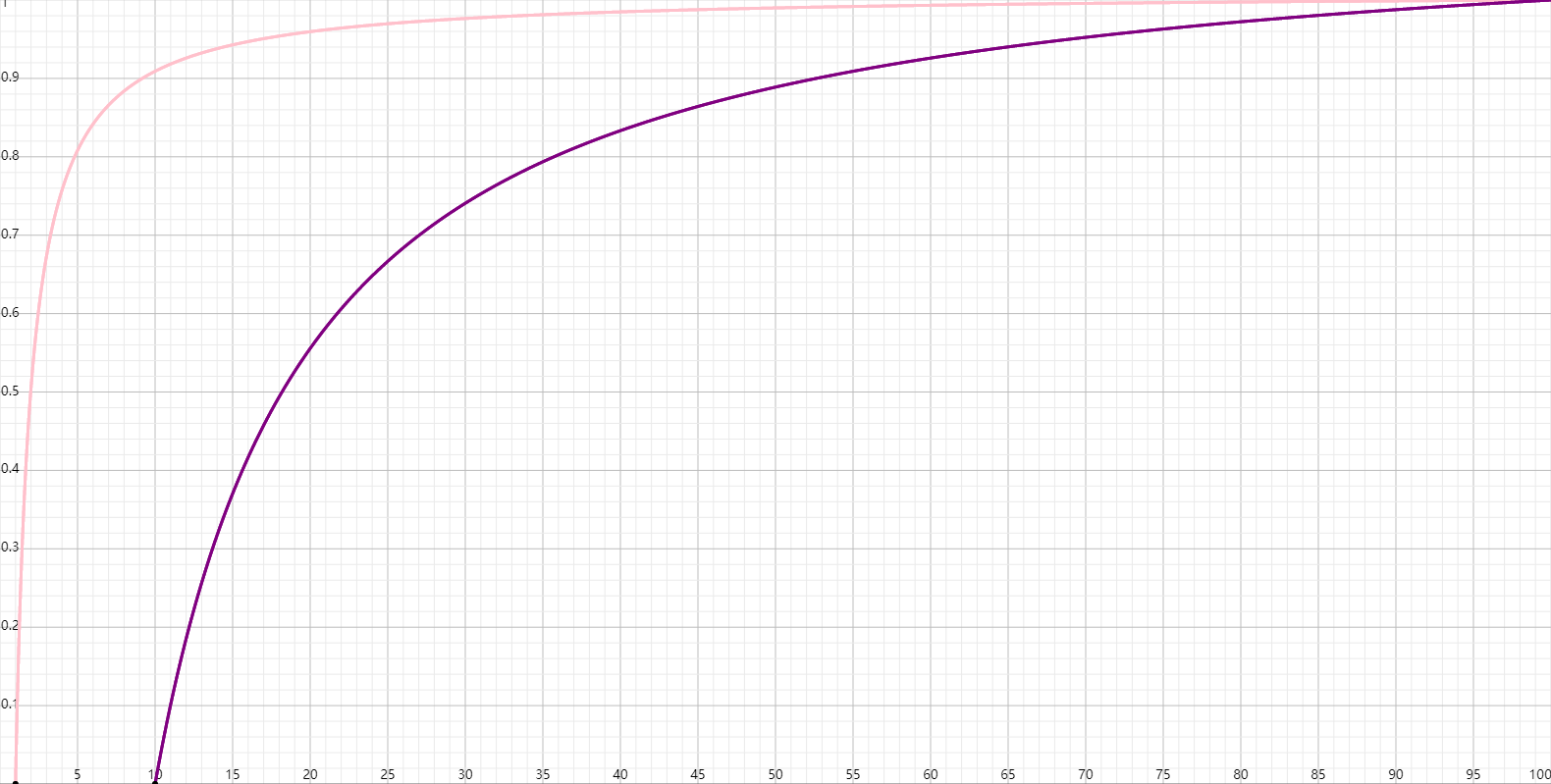
左边的曲线是((n=1,f=100)),右边的曲线是((n=10,f=100))。不难看出,当(n)和(f)的差距越小时,变换后的(z')精度更高。
在进行投影变换之后,透视除法之前,这时候坐标系称作齐次剪裁空间或者投影空间。在透视除法之后,被称作标准设备坐标系。