100+70+0=170。这套题早就被上传到BZOJ上了,可惜我一到都没做过。
BZOJ4765 普通计算姬
小G的计算姬可以解决这么个问题:给定一棵n个节点的带权树,节点编号为1到n,以root为根,设sum[p]表示以点p为根的这棵子树中所有节点的权值和。计算姬支持下列两种操作:
- 给定两个整数u,v,修改点u的权值为v。
- 给定两个整数l,r,计算sum[l]+sum[l+1]+....+sum[r-1]+sum[r]
尽管计算姬可以很快完成这个问题,可是小G并不知道它的答案是否正确,你能帮助他吗?
N<=10^5,M<=10^5
题解
分块。
查询就整块答案+边角余料,对于边角余料我直接树状数组。
我对每个元素维护他到根的链上每个块中的元素出现了多少次,这样修改就扫一遍所有块就行了。
这样空间会很卡,还必须开 unsigned long long,这出题人真的毒。
#include<bits/stdc++.h>
using namespace std;
template<class T> T read(){
T x=0;char c=getchar();
while(!isdigit(c)) c=getchar();
for(;isdigit(c);c=getchar()) x=x*10+c-'0';
return x;
}
template<class T> T read(T&x){
return x=read<T>();
}
#define co const
#define il inline
typedef unsigned long long LL;
co int N=100000+1,M=599+1;
int n,m,val[N];
vector<int> to[N];
int pos[N],dfn,lst[N];
namespace T{
LL sum[N];
il void change(int p,int v){
for(int i=p;i<=n;i+=i&-i) sum[i]+=v;
}
il LL query(int p){
LL ans=0;
for(int i=p;i;i-=i&-i) ans+=sum[i];
return ans;
}
}
int blo,num,bel[N];
int L[M],R[M],cnt[N][M];
LL sum[M];
void dfs(int x,int fa){
pos[x]=++dfn,T::change(pos[x],val[x]);
copy(cnt[fa]+1,cnt[fa]+num+1,cnt[x]+1),++cnt[x][bel[x]];
for(int i=1;i<=num;++i) sum[i]+=(LL)val[x]*cnt[x][i]; // edit 1:long long
for(int i=0;i<(int)to[x].size();++i){
int y=to[x][i];
if(y==fa) continue;
dfs(y,x);
}
lst[x]=dfn;
}
int main(){
freopen("common.in","r",stdin),freopen("common.out","w",stdout);
read(n),read(m);
blo=ceil(sqrt(n)/1.9),num=(n+blo-1)/blo;
for(int i=1;i<=num;++i) L[i]=R[i-1]+1,R[i]=min(i*blo,n);
for(int i=1;i<=n;++i){
read(val[i]);
bel[i]=(i+blo-1)/blo;
}
int root;
for(int i=1;i<=n;++i){
int x=read<int>(),y=read<int>();
if(!x) {root=y;continue;}
to[x].push_back(y),to[y].push_back(x);
}
dfs(root,0);
while(m--){
if(read<int>()==1){
int x=read<int>(),v=read<int>();
T::change(pos[x],v-val[x]);
for(int i=1;i<=num;++i) sum[i]+=(LL)(v-val[x])*cnt[x][i]; // edit 1
val[x]=v;
}
else{
int l=read<int>(),r=read<int>();
LL ans=0;
if(bel[l]==bel[r]){
for(int i=l;i<=r;++i) ans+=T::query(lst[i])-T::query(pos[i]-1);
}
else{
for(int i=bel[l]+1;i<=bel[r]-1;++i) ans+=sum[i];
for(int i=l;i<=R[bel[l]];++i) ans+=T::query(lst[i])-T::query(pos[i]-1);
for(int i=L[bel[r]];i<=r;++i) ans+=T::query(lst[i])-T::query(pos[i]-1);
}
printf("%llu
",ans);
}
}
return 0;
}
实际上可以不用树状数组,对 DFS 序再次分块,维护前缀和即可 O(1)。
BZOJ4766 文艺计算姬
文艺计算姬能计算一个带标号完全二分图的生成树个数。更具体地,给定一个一边点数为n,另一边点数为m,共有n*m条边的带标号完全二分图K_{n,m},计算姬能快速算出其生成树个数。小W不知道计算姬算的对不对,你能帮助他吗?
1 <= n,m,p <= 10^18
题解
考试的时候手玩70分巨爽。
回想起来我学习矩阵树还是初中的时候,那时我还不会在BZOJ上面找题做。不然我绝对会把这道经典题做了。
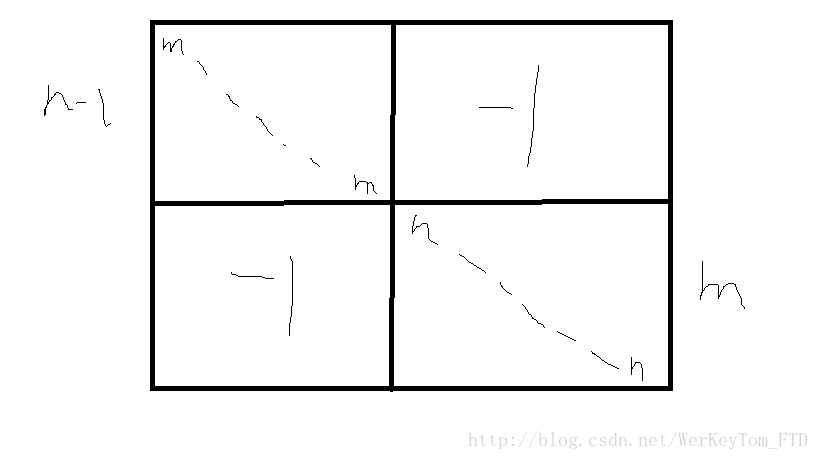
先把上面 n-1 行每一行都加到第 n 行去。 然后第 n 行变成 n-1 个 m-1 然后一个 1 再来 m-1 个 1-n。
把下面 m-1 行每一行都加到第 n 行去。 然后第 n 行变成只有后 m 个位置是 1。
把第 n 行加到前 n-1 行去,就把后面那堆-1消掉了。
然后变成下三角矩阵,行列式就是主对角线的乘积。 (ans=n^{m-1}m^{n-1})。
#include<bits/stdc++.h>
using namespace std;
template<class T> T read(){
T x=0,w=1;char c=getchar();
for(;!isdigit(c);c=getchar())if(c=='-') w=-w;
for(;isdigit(c);c=getchar()) x=x*10+c-'0';
return x*w;
}
template<class T> T read(T&x){
return x=read<T>();
}
#define co const
#define il inline
#define int long long
int mod;
il int mul(int a,int b){
int ans=0;
for(;b;b>>=1,a=(a+a)%mod)
if(b&1) ans=(ans+a)%mod;
return ans;
}
il int fpow(int a,int b){
int ans=1;
for(;b;b>>=1,a=mul(a,a))
if(b&1) ans=mul(ans,a);
return ans;
}
signed main(){
int n=read<int>(),m=read<int>();read(mod);
printf("%lld
",mul(fpow(n,m-1),fpow(m,n-1)));
return 0;
}
BZOJ4767 两双手
老W是个棋艺高超的棋手,他最喜欢的棋子是马,更具体地,他更加喜欢马所行走的方式。老W下棋时觉得无聊,便决定加强马所行走的方式,更具体地,他有两双手,其中一双手能让马从(u,v)移动到(u+Ax,v+Ay)而另一双手能让马从(u,v)移动到(u+Bx,v+By)。
小W看见老W的下棋方式,觉得非常有趣,他开始思考一个问题:假设棋盘是个无限大的二维平面,一开始马在原点(0,0)上,若用老W的两种方式进行移动,他有多少种不同的移动方法到达点(Ex,Ey)呢?两种移动方法不同当且仅当移动步数不同或某一步所到达的点不同。
老W听了这个问题,觉得还不够有趣,他在平面上又设立了n个禁止点,表示马不能走到这些点上,现在他们想知道,这种情况下马有多少种不同的移动方法呢?
答案数可能很大,你只要告诉他们答案模(10^9+7)的值就行。
保证Ax*By-Ay*Bx≠0
|Ax|,|Ay|,|Bx|,|By| <= 500, 0 <= n,Ex,Ey <= 500
题解
题面保证了给出的两个向量叉积为 0,就是说它们不平行。不平行的两个向量可以作为一组基底,根据向量唯一分解定理,原先平面上的所有点就获得了一个新坐标。于是问题变成了:从 (0,0) 走到 (n,m) ,中间不能经过指定的 k 个点,求方案数。
这是个简单的容斥 DP。记 (f[i]) 表示从 (0,0) 走到 i 号障碍点,中间不经过其它障碍点的方案数,这可以用组合数减去不合法的方案数求得。而不合法的方案必然存在第一个遇到的非 i 号障碍点 j ,于是有
其中 (g(i,j)) 表示第 (i) 个点到第 (j) 个点的方案数。这个就是个简单的组合数。
看到这个 DP 式,我觉得很熟悉。我大概做过这道题的简化版。
#include<bits/stdc++.h>
using namespace std;
template<class T> T read(){
T x=0,w=1;char c=getchar();
for(;!isdigit(c);c=getchar())if(c=='-') w=-w;
for(;isdigit(c);c=getchar()) x=x*10+c-'0';
return x*w;
}
template<class T> T read(T&x){
return x=read<T>();
}
#define co const
#define il inline
typedef long long LL;
co int mod=1000000000+7;
il int add(int a,int b){
return (a+=b)>=mod?a-mod:a;
}
il int mul(int a,int b){
return (LL)a*b%mod;
}
il int fpow(int a,int b){
int ans=1;
for(;b;b>>=1,a=mul(a,a))
if(b&1) ans=mul(ans,a);
return ans;
}
struct Vector {int x,y;};
il int cross(co Vector&a,co Vector&b){
return a.x*b.y-a.y*b.x;
}
bool trans(co Vector&A,co Vector&B,Vector&E){
int s=cross(A,B),x=cross(E,B);
if(x%s) return 0;
int t=cross(B,A),y=cross(E,A);
if(y%t) return 0;
E=(Vector){x/s,y/t};
return 1;
}
il bool operator<(co Vector&a,co Vector&b){
return a.x!=b.x?a.x<b.x:a.y<b.y;
}
co int N=501,M=1000000+1;
Vector E,A,B,S[N];
int fac[M],ifac[M],f[N];
il int binom(int n,int m){
return mul(fac[n],mul(ifac[m],ifac[n-m]));
}
int main(){
read(E.x),read(E.y);
int n=read<int>();
read(A.x),read(A.y),read(B.x),read(B.y);
if(!trans(A,B,E)) {puts("0");return 0;}
for(int i=1;i<=n;++i){
read(S[i].x),read(S[i].y);
if(!trans(A,B,S[i])||S[i].x<0||S[i].x>E.x||S[i].y<0||S[i].y>E.y) --n,--i;
}
sort(S+1,S+n+1),S[++n]=E;
// for(int i=1;i<=n;++i) cerr<<i<<" = "<<S[i].x<<" "<<S[i].y<<endl;
fac[0]=1;
for(int i=1;i<M;++i) fac[i]=mul(fac[i-1],i);
ifac[M-1]=fpow(fac[M-1],mod-2);
for(int i=M-2;i>=0;--i) ifac[i]=mul(ifac[i+1],i+1);
for(int i=1;i<=n;++i){
f[i]=binom(S[i].x+S[i].y,S[i].x);
for(int j=1;j<i;++j){
int dx=S[i].x-S[j].x,dy=S[i].y-S[j].y;
if(dx<0||dy<0) continue;
f[i]=add(f[i],mod-mul(f[j],binom(dx+dy,dx)));
}
}
printf("%d
",f[n]);
return 0;
}
说一下如何向量分解。假设两个基向量是 (i,j),新向量分解的结果是 (xi+yj),考虑以下式子
这样就不用解方程了,虽然效果都一样。