P1587 [NOI2016]循环之美
题目描述
牛牛是一个热爱算法设计的高中生。在他设计的算法中,常常会使用带小数的数进行计算。牛牛认为,如果在 $k$ 进制下,一个数的小数部分是纯循环的,那么它就是美的。现在,牛牛想知道:对于已知的十进制数 $n$ 和 $m$,在 $k$ 进制下,有多少个数值上互不相等的纯循环小数,可以用分数 $frac xy$ 表示,其中 $1≤x≤n,1≤y≤m$,且 $x,y$是整数。一个数是纯循环的,当且仅当其可以写成以下形式:
$a.dot{c_1} c_2 c_3 dots c_{p - 1} dot{c_p}$
其中,$a$ 是一个整数,$p≥1$;对于 $1≤i≤p$,$c_i$ 是 $k$ 进制下的一位数字。
例如,在十进制下,$0.45454545……=0.dot {4} dot {5}$是纯循环的,它可以用 $frac {5}{11}$、$frac{10}{22}$ 等分数表示;在十进制下,$0.1666666……=0.1dot6$则不是纯循环的,它可以用 $1/6$ 等分数表示。需要特别注意的是,我们认为一个整数是纯循环的,因为它的小数部分可以表示成 $0$ 的循环或是 $k-1$ 的循环;而一个小数部分非 $0$ 的有限小数不是纯循环的。
输入输出格式
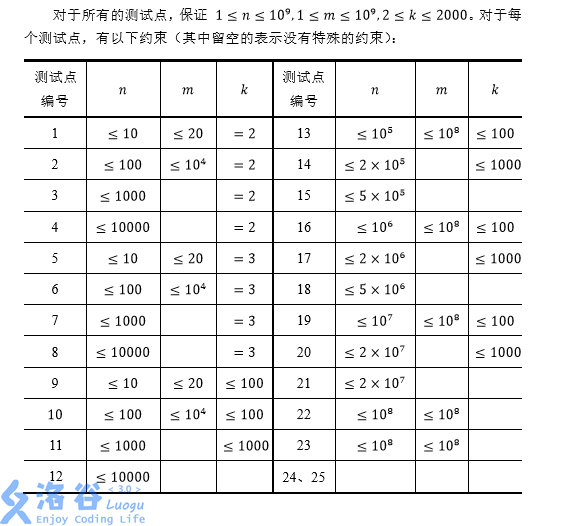
输入格式:只有一行,包含三个十进制数N,M,K意义如题所述,保证 1≤n≤10^9,1≤m≤10^9,2≤k≤2000
输出格式:一行一个整数,表示满足条件的美的数的个数。
输入输出样例
说明
满足条件的数分别是:
1/1=1.0000……
1/3=0.3333……
2/1=2.0000……
2/3=0.6666……1/1 和 2/2 虽然都是纯循环小数,但因为它们相等,因此只计数一次;同样,1/3 和 2/6 也只计数一次。
这部分将提供一个将分数化为对应的小数的方法,如果你已经熟悉这个方法,你不必阅读本提示。
分数可以通过除法,用分子除以分母化为对应的小数。有些分数在除法过程中无法除尽,这样的分数在不断进行的除法过程中余数一定会重复出现。从商数的个位所对应的余数起,设第一次重复出现的余数前两次出现的位置所对应的商数位分别是小数点后第 a位和小数点后第 b 位(特殊地:如果其中一个对应的商数位是个位,则认为 a=0;不妨设 a<b),则其循环部分可以用小数点后第 a+1位到小数点后第 b位的循环来表示。
例如:在十进制下,将 511转化为小数时,个位开始的商数依次为 4,5,4,…,对应的余数分别为 6,5,6,…。余数第一次重复出现的位置是个位和小数点后第 2 位,那么 a=0,b=2
a=0,b=2即其循环部分可以用小数点第 1位到第 3位来表示。表示为:511=0.45454545…=0.4˙5˙。
在十进制下,将 16 转化为小数时,个位开始的商数依次为 1,6,6,…,对应的余数分别为 4,4,4,…。余数第一次重复出现的位置是小数点后第 1 位和小数点后第 2 位,即其循环部分可以用小数点后第 2 位来表示。表示为:16=0.1666……=0.16˙。
需要注意的是:商数重复出现并不代表进入了循环节。
Kelin的题解
题意:求(sum_{x=1}^nsum_{y=1}^mfrac{x}{y})在(k)进制下能表示成循环节从第一位小数开始的无限循环小数或整数的最简分数个数
假设(frac{x}{y})的循环节长度为(l),则$ {frac{xk^l}{y}}={frac{x}{y}}$。
这里大括号表示其小数部分,意思就是把小数点往后挪(l)位,小数部分还是相同。比如(1.123123ldots)小数点往后挪3位变成(1123.123ldots)
参照10进制下小数点往后挪 (l) 位就是乘以 (10^l),那么 (k) 进制下小数点往后挪 (l) 位就是乘以 (k^l)
题目要求最简分数,所以 (gcd(x,y)=1)
-
考虑处理 ([gcd(i,j)=1])
观察式子,后面那个部分很支持整除分块,所以往这方面考虑。
设(f(n)=sum_{i=1}^n[gcd(i,k)=1]=lfloorfrac nk floorvarphi(k)+f(n mod k))。可以(O(klog k))预处理(f(1sim k))。
-
考虑分析式子
我们可以把(k)表示成(p^aq),假设(p)是(k)最小的质因子。对于1到(k)中每一个数可以预处理出他的(p,q)。设
因为(p)是质数,所以(gcd(d,p)=1)或(p)。考虑容斥,在满足 (gcd(d,q)=1)的(mu(d))中减去也满足((d,p)=p)的。即
当(gcd(d,p) eq 1)时(mu(dp)=0),所以(d)要满足((d,p)=1)
因为(mu)是积性函数,所以拆开得
边界是(g(0,k)=0),以及(g(n,1)=sum_{d=1}^nmu(d))直接杜教筛。
复杂度是 (O) (( (k) 的质因子个数) (sqrt n+n^{frac{2}{3}}) )
#include<bits/stdc++.h>
#define il inline
#define co const
template<class T>T read(){
T data=0,w=1;char ch=getchar();
for(;!isdigit(ch);ch=getchar())if(ch=='-') w=-w;
for(;isdigit(ch);ch=getchar()) data=data*10+ch-'0';
return data*w;
}
template<class T>il T read(T&x) {return x=read<T>();}
typedef long long LL;
using namespace std;
co int N=1e6+1,K=2001;
int n,m,k;
int pri[N],tot,mu[N];
int f[K],p[K],q[K];
int gcd(int a,int b){
return b==0?a:gcd(b,a%b);
}
void init(){
pri[1]=mu[1]=1;
for(int i=2;i<N;++i){
if(!pri[i]) pri[++tot]=i,mu[i]=-1;
for(int j=1;j<=tot&&i*pri[j]<N;++j){
pri[i*pri[j]]=1;
if(i%pri[j]==0){
mu[i*pri[j]]=0;
break;
}
mu[i*pri[j]]=-mu[i];
}
}
for(int i=2;i<N;++i) mu[i]+=mu[i-1];
for(int i=1;i<=k;++i) f[i]=f[i-1]+(gcd(i,k)==1);
// cerr<<"fk="<<f[k]<<endl;
for(int i=2;i<=k;++i){
for(int j=1;j<=tot;++j)
if(i%pri[j]==0) {p[i]=pri[j];break;}
for(q[i]=i/p[i];q[i]%p[i]==0;) q[i]/=p[i];
// if(k-i<=20) cerr<<i<<" p="<<p[i]<<" q="<<q[i]<<endl;
}
}
il int F(int n){
return n/k*f[k]+f[n%k];
}
typedef pair<int,int> pii;
map<pii,int> sg;
int G(int n,int k){
if(!n||n<N&&k==1) return mu[n];
if(sg.count(pii(n,k))) return sg[pii(n,k)];
if(k==1){
int ans=1;
for(int l=2,r;l<=n;l=r+1){
r=n/(n/l);
ans-=(r-l+1)*G(n/l,1);
}
return sg[pii(n,k)]=ans; // edit 1
}
return sg[pii(n,k)]=G(n,q[k])+G(n/p[k],k);
}
int main(){
read(n),read(m),read(k);
init();
// cerr<<"gnk="<<G(n,k)<<endl;
// cerr<<"fm="<<F(m)<<endl;
LL ans=0;
for(int l=1,r;l<=min(n,m);l=r+1){
r=min(n/(n/l),m/(m/l));
ans+=(LL)(G(r,k)-G(l-1,k))*(n/l)*F(m/l); // edit 2:(n/l)
}
printf("%lld
",ans);
return 0;
}
这题我n/k忘带括号然后WA了。现在想想下取整除法只有分母具有结合律。