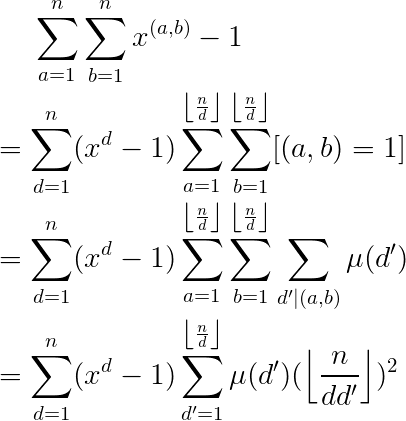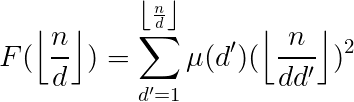题目简洁明了
给定(x,n),多组询问,求
[sum_{i=1}^nsum_{j=1}^n gcd(x^i-1,x^j-1)
]
对(1e9+7)取模,(x,n<=1e6)
首先先化一下里面这个东西
[(x^i-1,x^j-1)
]
我们用更相减损术来做
[(x^i-1,x^j-1)
]
[=(x^j-1-x^i+1,x^i-1)
]
[=(x^j-x^i,x^i-1)=(x^ix^{j-i}-x^i,x^i-1)
]
[=(x^i(x^{j-i}-1),x^i-1)
]
非常显然的是(x^i)和(x^i-1)是互质的,又因为((a imes c,b)=(a,b)[(b,c)=1])
所以上面那个东西就是
[(x^{j-i}-1,x^i-1)
]
发现指数上符合(gcd)的性质,于是我们可以知道这个式子迭代下去就是
[x^{(i,j)}-1
]
所以我们现在要求的是
[sum_{i=1}^nsum_{j=1}^nx^{(i,j)}-1
]
这肯定是要反演了,有两种做法,一种是我自己(yy)的(O(Tn^{frac{2}{3}})),还有就是(O(n+Tsqrt{n}))的正解
先来看看我(yy)的做法,我们可以把(-1)提出来,只需要求
[sum_{i=1}^nsum_{j=1}^nx^{(i,j)}
]
设
[f(d)=sum_{i=1}^nsum_{j=1}^n[(i,j)=d]
]
于是
[ans=sum_{i=1}^nf(i)x^i
]
[=sum_{i=1}^nsum_{i|d}mu(frac{d}{i})left lfloor frac{n}{d}
ight
floor^2x^i
]
[=sum_{d=1}^nleft lfloor frac{n}{d}
ight
floor^2sum_{i|d}mu(frac{d}{i})x^i
]
设(F(d)=sum_{i|d}mu(frac{d}{i})x^i)
[ans=sum_{d=1}^nleft lfloor frac{n}{d}
ight
floor^2F(d)
]
我们需要快速求(F)函数的前缀和,之后就可以愉快的整除分块了
考虑一下杜教筛
我们再设一个函数(h(i)=x^i)
于是
[F=mu imes h
]
反演得
[F imes I=h
]
往杜教筛的套路里一放
[S(n)=sum_{i=1}^nh(i)-sum_{i=2}^nI(i)S(left lfloor frac{n}{i}
ight
floor)
]
前面的(h)的前缀和就是一个等比数列求和,(I)也很好算
于是可以杜教筛直接硬上了
但是感觉这个复杂度有点感人啊
再来看看正解
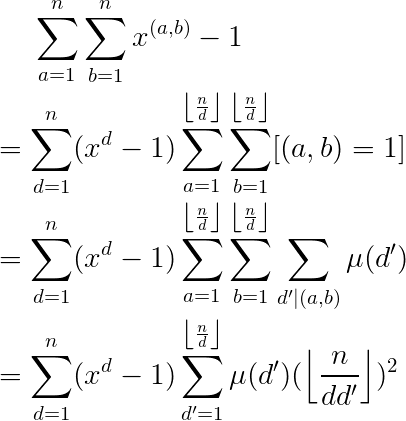
我们完全可以把后面的搞成一个函数
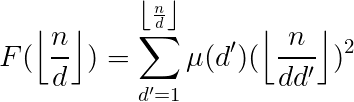
把(left lfloor frac{n}{d}
ight
floor)换成(x),就惊奇的发现
[F(x)=sum_{d=1}^xmu(d)left lfloor frac{x}{d}
ight
floor^2
]
发现(F)函数和(n)没什么关系,于是我们可以提前预处理(F)啊
但是(F)看起来不好求的样子
先抄结论
[F(x)=2 imes (sum_{i=1}^xvarphi(i))-1
]
这一步证明就先咕咕咕了
至于代码,肯定也是要咕咕咕的
因为我就根本不准备写
(upd)
感受到了慎老师和成爷爷的强大
先来看看慎老师的神仙做法
那就是不反演
发现我们化式子化到了这一步
[sum_{d=1}^n x^dsum_{i=1}^{left lfloor frac{n}{d}
ight
floor}sum_{j=1}^{left lfloor frac{n}{d}
ight
floor}[(i,j)=1]
]
看到后面那个东西就想用反演求真实思维僵化
其实最开始还学过一种叫做欧拉函数强行搞的东西
后面那个不就是
[2 imes sum_{i=1}^{left lfloor frac{n}{d}
ight
floor}varphi(i)-1
]
啊啊啊啊啊啊啊
你看我连这个都不会了,真是退役预定了
(upd)
又来更成爷的做法了
成爷的做法非常暴力就是直接搞上面的式子
[F(x)=sum_{d=1}^xmu(d)left lfloor frac{x}{d}
ight
floor^2
]
这个式子看起来确实不是很好求,因为单次求一下是(O(sqrt{n}))的
所以需要考虑从(F(x))推到(F(x+1))