1.定义:
如果一个系统由n个变量和m个约束条件组成,形成m个形如ai-aj≤k的不等式(i,j∈[1,n],k为常数),则称其为差分约束系统(system of difference constraints)。亦即,差分约束系统是求解关于一组变量的特殊不等式组的方法。
求解差分约束系统,可以转化成图论的单源最短路径(或最长路径)问题。
2. 数形结合
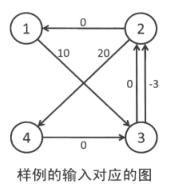
若一个系统由 n 个变量和 m 个不等式组成,并且这 m 个不等式对应的系数矩阵中每一行有且仅有一个 1 或 -1 ,其它的都为 0,这样的系统称为差分约束(difference constraints)系统。例如:
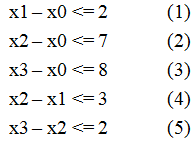
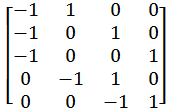
观察 x [ i ] - x [ j ] <= a [ k ], 将 x [ j ] 移至不等号的右边,即 x [ i ] <= x [ j ] + a [ k ].再进行同等的形式变换 d [ u ] + w (u, v) >= d [ v ]. 这时候联想到 SPFA 的松弛操作:
if (d[u] + w(u, v) < d[v) { d[v] = d[u] + w(u, v); }
对比上面的两个不等式,发现两个不等式的不等号正好相反,但思考一下其实它们的逻辑是一致的,这是因为SPFA的松弛操作是在满足小于的情况下进行的松弛,最后力求达到 d [ u ] + w (u, v) >= d [ v ] 的效果。所以我们可以将每个不等式转化为图上的有向边。
对于每个不等式 x [ i ] - x [ j ] <= a [ k ], 从结点 j 到 i 建立一条 j -> i 的有向边,边的权值为 a [ k ], 求 x [ n - 1 ] - x [ 0 ] 的最大值就是求 0 -- n - 1 的最短路。
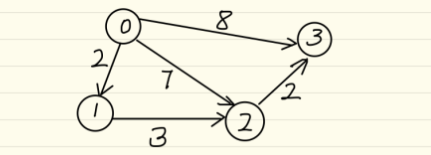
3. 解的存在性
在最短路的问题中,会出现负圈或者不可达的情况,所以在不等式转化到图上时也可能出现上述问题。如果路径中出现了负圈,则表示最短路无限小,即不存在最短路,那么 x [ t ] - x [ s ] <= T , T 无限小, 那么 x [ t ] - x [ s ] 的最大值不存在。
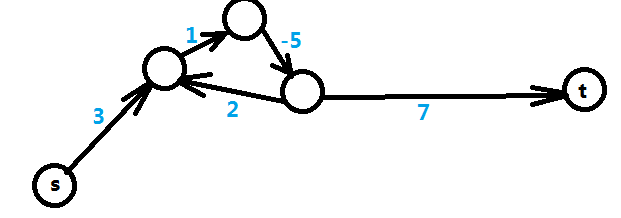
如果是从起点 s 无法到达 t 的情况,则表明 x [ t ] 和 x [ s ] 之间并没有约束条件,这种情况下 x [ t ] - x[ s ] 的最大值是无限大,解有无穷个。
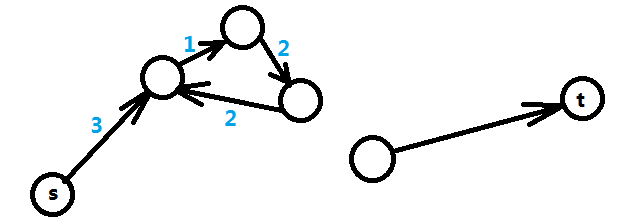
综上所述:差分约束系统的解有三种情况:有解, 有无穷多解,无解。
4. 最大值 --> 最小值
当我们把上面的不等式组中 “ <= ” 全部变为 " >= ", 则就变为求 0 -- n - 1 的最长路。
5. 不等式的标准化
首先统一不等号的方向,如果求最大值,将不等号全部变为 “ <= ”,建图后求最短路;
如果求最小值,将不等号全部变为 " >= ",建图后求最长路。
如果有形如 A - B = C 这样的等式,则将其转化为:
A - B >= C
A - B <= C
再将其中的一种不等号反向,建图即可。
如果变量都是定义在整数域上, 那么遇到 A - B < C 这样的不带等号的不等式, 我们需要将其转化为 “ <= ” 或 “ >= ”, 即 A - B <= C - 1。
6. 差分约束的经典应用
(1) 线性约束
线性约束一般是在一维空间中给出一些变量(一般是定义位置),然后告诉你某两个变量的约束关系求两个变量 a 和 b 的差值的最大值或最小值。
例题: N 个 人编号为 1 - N,并按照编号排成一列,任何两个人的位置不重合。给定一些约束条件:
X 组约束条件 Ax 和 Bx 的距离不大于 Cx 。
Y组约束条件 Ay 和 By 的距离不小于 Cy。
如果这样的排列存在,求1 - N 的最长可能距离,如果不存在输出 -1,如果无限长输出 -2.
令 d [ x ] 为第 x 个人的位置,根据题意有如下的约束条件:
对于X组,有d[ Bx ] - d[ Ax ] <= Cx;
对于Y组,有d[ By ] - d[ Ay ] >= Cy;
任意两人位置不重合,有 d[ x ] - d [ x - 1] >= 1
我们要求的是 d[ N ] - d[ 1 ] 的最大值,即表示为 d[ N ] - d[ 1 ] <= T. 将所有的不等式转化为 “ <= ” 的形式:
d[ Bx ] - d[ Ax ] <= Cx;
d[ Ay ] - d[ By ] <= -Cy;
d[ x - 1 ] - d[ x ] <= -1;
对于 d[ x ] - d[ y ] <= z ,令 z = w(x, y),那么有 d[ x ] <= d[ y ] + w(x, y) ,所以当 d[ x ] > d[ y ] + w(x, y)时,更新 d[ x ] 的值,这就对应了最短路的松弛操作,于是问题就转化成了求 1 到 N 的最短路。
对于所有不等式 d[ x ] - d[ y ] <= z,从 y 向 x 建立一条权值为 z 的有向边。然后从 1 出发,利用SPFA求到各个点的最短路,如果 1 到 N 不可达,说明最短路无限长; 如果某个点进入队列的次数 >= N 次,则必定存在负圈,即没有最短路,否则 最后的的 d[ N ] 就是最短路。
(2) 区间约束
例题:POJ-1201 Intervals
给定 n 个整数闭区间 和 每个区间中至少有多少整数需要被选中,每个区间的范围为 [ a, b ],(0 <= a <= b <= 50000) 并且至少 c 个点被选中, 求 [0, 50000] 中至少需要多少点被选中。例如 : 3 6 2 表示[ 3, 6]区间里至少选择 2 个点,有C24种情况。
这类问题没有线性约束那么明显,需要将问题转化一下。考虑到最后需要求的是一个完整区间内至少有多少点被选中,我们试着用 d [ i ] 表示 [0, i]区间至少有多少点能被选中,显然 d[ - 1 ] = 0.对于每个区间描述,可以表示成 d[ b ] - d[ a ] >= c,即 d[ b ] >= d[ a ] + c, 而我们的目标是 d[ 50000 ] - d[ - 1 ] >= T 这个不等式中的 T,将所有区间描述转化成图后求 -1 到 50000 的最长路。
这里忽略了一些要素,因为 d[ i ] 描述了一个求和函数,所以对于 d[ i ] 和 d[ i - 1 ] 是有限制的。考虑到每个点都有选和不选两种情况,所以 d[ i ] 和 d[ i - 1 ] 需要满足 0 <= d[ i ] - d[i - 1] <= 1 (即第 i 个数是选或不选)。
这样一来,还需要加入 50000 * 2 = 100000 条边,由于数据较大需要用 SPFA 优化,由于 -1 不能映射到小标,所以可以将所有点右移一位。
(3) 未知条件约束
未知条件约束是指在不等式的右边不一定是一个常数,可能是个未知数,通过枚举这个未知数,然后对不等式转化为差分约束进行求解。
例题:POJ-1275 Cashier Employment
在一家超市里,每个时刻都需要有营业员看管, R(i) (0 <= i <= 24)表示从 i 时刻开始到 i + 1 时刻结束需要的营业员的数目,现在有 N 个人申请这项工作,并且每个申请者都有一个起始工作时间 ti ,如果第 i 个申请者被录用,那么他会连续工作 8 小时。现在要求选择一些申请者录用,使得任一时刻 i ,营业员数目都能 ≥ R(i)。
i = 0,1,...,23,分别对应时刻[i, i + 1],特别的,23 表示的是[23, 0],并且有些申请者的工作时间可能会跨天。
a[ i ] 表示第 i 时刻开始工作的人数 -- 未知量
b[ i ]表示第 i 时刻能够开始工作的人数上限 -- 已知量
R[ i ]表示第 i 时刻必须值班的人数 -- 已知量
那么第 i 时刻到第 i + 1 时刻还在工作的人满足下面两个不等式(每人工作8小时)
a[i - 7] + a[ i - 6] + ... + a[ i ] ≥ R[ i ] i ≥ 7
(a[ 0 ] + ... + a[ i ]) + (a[ i + 17 ] + ... + a[ 23 ]) ≥ R[ i ] 0 ≤ i < 7
对于从第 i 时刻开始工作的人,满足以下不等式:
0 ≤ a[ i ] ≤ b[ i ] 0 ≤ i < 24
令 s[ i ] = a[ 0 ] + .. + a[ i ],特别的,s[ - 1 ] = 0,上面三个式子用 s[ i ] 来表示,如下:
s[ i ] - s[ i - 8 ] ≥ R[ i ] i ≥ 7 (1)
s[ i ] + s[ 23 ] - s[ i + 16 ] ≥ R[ i ] 0 ≤ i < 7 (2)
0 ≤ s[ i ] - s[ i - 1 ] ≤ b[ i ] 0 ≤ i < 24 (3)
仔细观察不等式(2),有三个未知数,这里的 s[ 23 ] 就是未知量,所以还无法转化成差分约束求解,但是和 i 相关的变量只有两个,对于s[ 23 ]的值可以进行枚举,令 s[ 23 ] = T, 则有以下几个不等式:
s[ i ] - s[ i - 8 ] ≥ R[ i ]
s[ i ] - s[ i + 16 ] ≥ R[ i ] - T
s[ i ] - s[ i - 1 ] ≥ 0
s[ i - 1 ] - s[ i ] ≥ -b[ i ]
对于所有的不等式 s[ y ] - s[ x ] ≥ c,建立一条权值为 c 的边 x -> y,于是问题就转化成了求从原点 -1 到终点 23 的最长路。
我们还少了一个条件,即 s[ 23 ] = T,我们需要把它转化为不等式,由于设定 s[ -1 ] = 0,所以 s[ 23 ] - s[ -1 ] = T,转化为不等式:
s[ 23 ] - s[ 1 ] ≥ T
s[ -1 ] - s[ 23 ] ≥ -T
将这两条边补到原图中,求出的最长路 s[ 23 ] = T,表示 T 就是满足条件的一个解,由于 T 的值是从小到大枚举的 (0 ≤ T ≤ N),所以第一个满足条件的解就是答案。
最后观察申请者的数量,当 i 个申请者能够满足条件的时候, i + 1 个申请者必定可以满足条件,所以申请者的数量是单调的,可以对 T 进行二分枚举,将枚举复杂度从 0(N)降为 0(log N)
补题:
1. Layout( POJ 3169 )



很明显的差分约束,所要求的是 N 到 1 的最大距离,即 d[ N ] - d[ 1 ] ≤ T, 根据题意得出不等式:
BL - AL ≤ DL
AD - BD ≤ DD
转化为求图的最短路

int N, ML, MD; int AL[MAX_ML], BL[MAX_ML], DL[MAX_ML]; int AD[MAX_MD], BD[MAX_MD], DD[MAX_MD]; int d[MAX_N]; //SPFA typedef pair<int, int> P; struct edge{ int to; int cost; }; vector<edge> G[MAX_N]; //int d[MAX_N]; int vis[MAX_N]; //被访问的次数 bool inq[MAX_V]; //结点 i 是否在队列中 void Bellman_Ford() { fill(d, d + N, INF); d[0] = 0; for (int k = 0; k < N; k++) { // 从 i+1 到 i 的权值为 0 for (int i = 0; i + 1 < N; i++) if (d[i + 1] < INF) d[i] = min(d[i], d[i + 1]); // 从AL到BL的权值为DL for (int i = 0; i < ML; i++) if (d[AL[i] - 1] < INF) d[BL[i] - 1] = min(d[BL[i] - 1], d[AL[i] - 1] + DL[i]); // 从BD到AD的权值为 -DD for (int i = 0; i < MD; i++) if (d[BD[i] - 1] < INF) d[AD[i] - 1] = min(d[AD[i] - 1], d[BD[i] - 1] - DD[i]); } int res = d[N - 1]; if (d[0] < 0) res = -1; // 存在负圈,无解 else if (res == INF) res = -2; printf("%d ", res); } int SPFA(int s) { memset(d, INF, sizeof(d)); memset(vis, 0, sizeof(vis)); memset(inq, false, sizeof(inq)); queue<P> q; q.push(P(d[s], s)); d[s] = 0; inq[s] = true; while (!q.empty()) { P p = q.front(); q.pop(); int v = p.second; inq[v] = false; if (vis[v]++ > N) return -1; for (int i = 1; i < G[v].size(); i++) { edge e = G[v][i]; if (d[e.to] > d[v] + e.cost) { d[e.to] = d[v] + e.cost; if (!inq[e.to]) { inq[e.to] = true; q.push(P(d[e.to], e.to)); } } } } if (d[N] == INF) return -2; else return d[N]; } int main() { cin >> N >> ML >> MD; for (int i = 0; i < ML; i++) { int AL, BL, DL; cin >> AL >> BL >> DL; G[AL].push_back((edge){BL, DL}); } for (int i = 0; i < MD; i++) { int AD, BD, DD; cin >> AD >> BD >> DD; G[BD].push_back((edge){AD, -DD}); } printf("%d ",SPFA(1)); return 0; }
本篇学习自:夜深人静写算法(四) - 差分约束
