转自:https://www.cnblogs.com/ECJTUACM-873284962/p/6880199.html 高斯消元模板
https://www.cnblogs.com/baiyi-destroyer/p/9473064.html 例题1
https://blog.csdn.net/lianai911/article/details/48464007?biz_id=102&utm_term=Flip%20Game%20%E9%AB%98%E6%96%AF%E6%B6%88%E5%85%83%E6%B3%95&utm_medium=distribute.pc_search_result.none-task-blog-2~all~sobaiduweb~default-0-48464007&spm=1018.2118.3001. 4187 例题2
https://blog.csdn.net/u011815404/article/details/88897724 例题3
https://blog.csdn.net/bless924295/article/details/53575836 例题4
高斯消元法
一 理论基础
① 定义:解 一个 线性方程组,对方程组的增广矩阵 施行初等行变换,变换后的矩阵所对应的方程组与原方程组同解,
这种解法称为 高斯消元法
② 需要用到的理论知识有:增广矩阵,初等行变换,行阶梯形矩阵,矩阵的秩
二,代码实现
① 首先我们需要根据题意列出方程组,然后根据方程组构造增广矩阵
② 根据初等行变换构造行阶梯形矩阵
③ 根据矩阵的秩,判断解的情况
具体解释我在代码中写的很清楚,这里提一下一点:k, 与矩阵的秩,与 COL
k:
在循环中,我们是通过 col 循环每一列,再用 k 去试探 主元的位置,
所以 k 在循环时,指向 上一列中主元所在行的下一行,即 当前列主元可能出现的位置。
k 在循环结束时,指向 行阶梯线的最下面一个台阶的下一行,由于 矩阵是从 0 开始的,
所以此时 k 可以在数值上 代表 行阶梯线的行数,所以还可以代表为 该矩阵的秩,所以还可以代表 方程组可解的个数
COL:
系数矩阵的列数,还可以代表 该方程组未知数的个数
所以:
k == COL :代表方程组的每一个未知数 刚好可解,即该方程组唯一可解
k < COL:代表方程组的未知数 有些是解不出来的,即该方程组有无穷解
k > COL:代表方程组的未知数,可解的个数大于未知数的个数 ,即该方程组有唯一解,且该方程组 多列 k-COL 组多余的方程。
无解:当方程中出现(0, 0, …, 0, a)的形式,且a != 0时,说明是无解的
下面是大神求解整数线性方程组的模板

#define _CRT_SECURE_NO_WARNINGS #include<stdio.h> #include<stdlib.h> #include<string.h> #include<math.h> #define mem(a,b) memset(a,b,sizeof(a)) #define N 105 int a[N][N]; /*不确定的变元:未知数(想要求解,但不知道能否解出来) 确定的变元:可求解的未知数 自由变元:无法求解的未知数 */ int x[N]; // 解集 bool free_x[N]; // 判断是否是不确定的变元 int free_num; // 自由变元的个数 int ROW, COL; // 行数,列数,注意 COL 没有包括 常数项向量那一列 void show(void) { puts(""); for (int i = 0; i < ROW; i++) { for (int j = 0; j < COL + 1; j++) { printf("%d ", a[i][j]); }puts(""); } } inline int gcd(int a, int b) { return b ? gcd(b, a%b) : a; } inline int lcm(int a, int b) { return a*b / gcd(a, b); } // 高斯消元法解方程组(Gauss-Jordan elimination). // 求解整数线性方程组的模板,浮点数把那个 return -2 去掉,改下数据类型就可 // (-2表示有浮点数解,-1表示无解,0表示唯一解,大于0表示无穷解,并返回自由变元的个数) int Gauss(void) { int k, col; /* 循环目的:求行阶梯形矩阵 循环变量:col ,循环每一列 k 代表 阶梯线的行数, k 始终指向阶梯线的下一行, 它是用来试探 当前循环的这一列的阶梯线应该画在哪里 循环结束条件是:阶梯线下一步将要扩展到超越 系数矩阵的边界,或是从行数或是从列数 总结起来就是:通过循环每一列,利用 k 记录阶梯线的位置(k 比阶梯线多了一行),将 k 以下的元素清零 */ for (k = 0, col = 0; k < ROW&&col < COL; k++, col++) { /* 找到第col列元素里面,绝对值最大的那个元素所在的那行与第k行交换.(为了在除法时减小误差) 即 在第一列中从第 k 行往下找到数值最大的数(包括第 k 行的元素),把该数所在的那一行移到第 k 行 在第二列中从第 k 行往下找到数值最大的数(包括第 k 行的元素),把该数所在的那一行移到第 k 行 即 选出该列最大元素值来当这一列的主元 */ /*为什么要选出最大值呢?这是因为在消元时,当主元包含小数时,在进行乘法或者除法时, 浮点数的运算就会产生误差,你主元越小,计算越多次,误差越大。 所以主元要选最大的,可以减少误差。 */ int max_r = k; for (int i = k + 1; i < ROW; i++) if (abs(a[i][col]) > abs(a[max_r][col])) max_r = i; if (max_r != k) for (int i = k; i <= COL; i++) { int t = a[k][i]; a[k][i] = a[max_r][i]; a[max_r][i] = t; } /*不止剪枝:该列中(阶梯下方的元素,包括阶梯线上的元素)的最大值为 0,说明阶梯下方 全为 0 则这一列不用处理,这一列不处理的话,说明该行已经处理完毕,可以用 k 继续试探下一行的主元位置 k--代表 减去一个主元,是要将for 循环增加的一个减回来,因为这一列没有主元*/ if (a[k][col] == 0) { k--; continue; } /*枚举要清零的行,用该列的主元所在的行 通过 行变换清零 阶梯线下的元素*/ for (int i = k + 1; i < ROW; i++) { if (a[i][col] != 0) { int LCM = lcm(abs(a[i][col]), abs(a[k][col])); int ta = LCM / abs(a[i][col]); // 主元 int tb = LCM / abs(a[k][col]); // 其他元 if (a[i][col] * a[k][col] < 0) tb = -tb; // 判断有无异号,ta 和 tb 皆可变号 for (int j = col; j < COL + 1; j++) // 变换是整个行都要变换的,不止当前 col 这一列 { a[i][j] = a[i][j] * ta - a[k][j] * tb; } } } } show(); /* ① 无解:当方程中出现(0, 0, …, 0, a)的形式,且a != 0时,说明是无解的。 循环结束后,col 不一定指向 COL, k 则必然指向 阶梯线的下一行, (但是这个循环是在 k < ROW 时发生的,此时 col 必然等于 COL, 原因是循环结束条件:k < ROW&&col < COL,既然 k < ROW,那么自然 col == COL) 所以 [k,ROW) 这个区间上的行,对应的系数矩阵上的元素都是 0 最后只要再判断一下 常数项向量 是否为 0, 就可以了 */ for (int i = k; i < ROW; i++) // [k,ROW) 这个区间上的行,都是 0,除了 a 还没判断 { if (a[i][col] != 0) // 判断 当前行对应的常数项向量是否为 0 return -1; } /*② 无穷解:条件是 k < COL, COL 代表:线性方程要求解的变元(就是未知数)的个数 k 代表:矩阵的秩,即可确定的变元的个数 (这里解释一下 k. 因为当循环结束时,k 依然指向行阶梯线的下一行, 但因为 k 是物理序号,与逻辑序号差 1 ,所以,此时 k 在数值上刚好等于 矩阵的秩) 所以 自由变元 = COL - k 但有些题目要 求判断哪些变元是不确定的,这里单独介绍下这种解法: 首先,自由变元有COL - k个。我们先把所有的变元视为不确定的,即 free_x[j] = 1, 通过回带,在每一行里尝试求解不确定变元。首先判断不该行中不确定变元的个数, 如果大于1个,则该行无法求解。如果只有1个变元,那么该变元即可求出。 然后将该不确定变元,变为确定变元,即 free_x[j] = 0, 最后每一行都循环结束的话,剩下都是 自由变元 */ if (k < COL) { for (int i = k - 1; i >= 0; i--) { int free_x_num = 0; // 用于 记录该行中的不确定的变元的个数 int free_index = 0; // 记录 不确定变元的列数 for (int j = 0; j < COL; j++) { // 第i行一定不会是(0, 0, ..., 0)的情况,因为这样的行是在第 k 行到第 ROW 行. // 同样,第i行一定不会是(0, 0, ..., a), a != 0的情况,这样的无解的. // free_x_num 用来记录这一行 自由变元的个数:free_index 用来记录这一行自由变元的 列数 // free_x 用来判断该数 是否是自由变元 if (a[i][j] != 0 && free_x[j]) free_x_num++, free_index = j; } if (free_x_num > 1) // 该行中的不确定的变元的个数 如果超过1个,则无法求解,进入到下一次循环 continue; // 回代 int t = a[i][COL]; // 该行末位的常数项向量中的元素 for (int j = 0; j < COL; j++) { if (a[i][j] != 0 && j != free_index) // 减去已知变元 t -= a[i][j] * x[j]; } x[free_index] = t / a[i][free_index]; // 解出这一行中唯一一个 不确定变元 free_x[free_index] = 0; // 不确定变元 被解开 变成确定变元 ,所以从自由变元中 删除 该变元 } return COL - k; } /*③ 唯一解:条件是 k == COL,即行阶梯阵形成了严格的上三角阵。 (注意这个三角不一定是沿着对角线的,因为 系数矩阵不一定是正方形,但它一定是等腰直角三角形 ) 由下往上 利用回代逐一 计算出Xn-1, Xn-2 ... X0 */ for (int i = k - 1; i >= 0; i--) { int t = a[i][COL]; // 回带 // 循环上三角中同一行的元素,将 矩阵的每一行 变成至多只有两个数:常数项一个 和 系数矩阵一个 for (int j = i + 1; j < COL; j++) { if (a[i][j] != 0) t -= a[i][j] * x[j]; // 减去已知变元 } if (t%a[i][i] != 0) // 说明有浮点数解,但无整数解. return -2; x[i] = t / a[i][i]; } return 0; } int main(void) { while (scanf("%d%d", &ROW, &COL) != EOF) { mem(a, 0), mem(x, 0); mem(free_x, 1); // 初始化为 不确定的变元. for (int i = 0; i < ROW; i++) // 增广矩阵 for (int j = 0; j < COL + 1; j++) // 要加上常数项向量 scanf("%d", &a[i][j]); free_num = Gauss(); if (free_num == -1) printf("无解! "); else if (free_num == -2) printf("有浮点数解,无整数解! "); else if (free_num > 0) { printf("无穷多解!自由变元个数为%d ", free_num); for (int i = 0; i < COL; i++) { if (free_x[i]) printf("x%d 是不确定的 ", i + 1); else printf("x%d:%d ", i + 1, x[i]); } } else for (int i = 0; i < COL; i++) printf("x%d:%d ", i + 1, x[i]); puts(""); } system("pause"); return 0; } /* 3 3 2 -1 3 1 4 2 5 4 2 1 2 5 */ /* 3 4 1 2 3 4 5 2 4 4 6 8 -1 -2 -1 -2 -3 */
异或方程组的模板

#define _CRT_SECURE_NO_WARNINGS #include<stdio.h> #include<stdlib.h> #include<string.h> #include<math.h> #define mem(a,b) memset(a,b,sizeof(a)) #define N 35 int a[N][N]; int x[N]; int free_x[N]; int f[N]; // 记录自由变元的行数 /* f[i]:第 i 个自由变元的列数,同时也是行数 记录的两种方法: ① 行阶梯矩阵的同一行全为 0 ② 无穷解,无法求解的变元 */ int ROW, COL; // 0 1 方程组下的高斯消元 int Gauss(void) { memset(free_x, 1, sizeof(free_x)); memset(x, 0, sizeof(x)); int k = 0, col = 0; int num = 0; for (; k < ROW&&col < COL; k++, col++) { int max_r = k; for (int i = k + 1; i < ROW; i++) if (abs(a[i][col]) > abs(a[max_r][col])) max_r = i; if (max_r != k) for (int i = 0; i < COL + 1; i++) { int t = a[max_r][i]; a[max_r][i] = a[k][i]; a[k][i] = t; } if (a[k][col] == 0) { k--; f[num++] = col; continue; } for (int i = k + 1; i < COL + 1; i++) { if (a[i][col] != 0) for (int j = col; j < COL; j++) { // a[i][j] = (a[i][j]%2 - a[k][j]%2 + 2) % 2; a[i][j] = a[i][j] ^ a[k][j]; } } } for (int i = k; i < ROW; i++) { if (a[i][COL] != 0) return -1; } if (k < COL) { for (int i = k - 1; i >= 0; i--) { int num = 0, index = 0; for (int j = 0; j < COL; j++) { if (a[i][j] && free_x[j]) { num++; index = j; } if (num > 1) continue; int t = a[i][COL] % 2; for (int j = 0; j < COL; j++) { if (a[i][j] && j != index) t = (t - a[i][j] * x[j] % 2 + 2) % 2; } x[index] = t / a[i][index] % 2; free_x[index] = 0; } int cnt = 0; for (int i = 0; i < COL; i++) if (free_x[i]) f[cnt++] = i; } return COL - k; } for (int i = k - 1; i >= 0; i--) { int t = a[i][COL]; for (int j = i + 1; j < COL; j++) { if (a[i][j] != 0) t = (t - a[i][j] * x[j] % 2 + 2) % 2; } x[i] = t / a[i][i] % 2; } return 0; } int main(void) { while (scanf("%d%d", &ROW, &COL) != EOF) { mem(a, 0), mem(x, 0); mem(free_x, 1); // 初始化为 不确定的变元. for (int i = 0; i < ROW; i++) // 增广矩阵 for (int j = 0; j < COL + 1; j++) // 要加上常数项向量 scanf("%d", &a[i][j]); int free_num = Gauss(); if (free_num == -1) printf("无解! "); else if (free_num == -2) printf("有浮点数解,无整数解! "); else if (free_num > 0) { printf("无穷多解!自由变元个数为%d ", free_num); for (int i = 0; i < COL; i++) { if (free_x[i]) printf("x%d 是不确定的 ", i + 1); else printf("x%d:%d ", i + 1, x[i]); } } else for (int i = 0; i < COL; i++) printf("x%d:%d ", i + 1, x[i]); puts(""); } system("pause"); return 0; }
例题:EXTENDED LIGHTS OUT
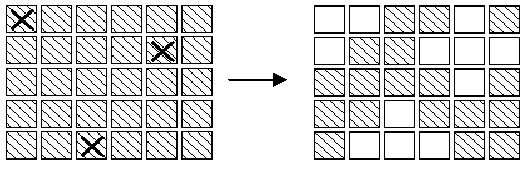
The aim of the game is, starting from any initial set of lights on in the display, to press buttons to get the display to a state where all lights are off. When adjacent buttons are pressed, the action of one button can undo the effect of another. For instance, in the display below, pressing buttons marked X in the left display results in the right display.Note that the buttons in row 2 column 3 and row 2 column 5 both change the state of the button in row 2 column 4,so that, in the end, its state is unchanged.
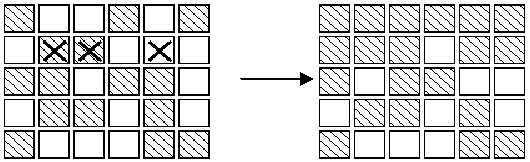
Note:
1. It does not matter what order the buttons are pressed.
2. If a button is pressed a second time, it exactly cancels the effect of the first press, so no button ever need be pressed more than once.
3. As illustrated in the second diagram, all the lights in the first row may be turned off, by pressing the corresponding buttons in the second row. By repeating this process in each row, all the lights in the first
four rows may be turned out. Similarly, by pressing buttons in columns 2, 3 ?, all lights in the first 5 columns may be turned off.
Write a program to solve the puzzle.
这个游戏有一些技巧:
1、按按钮的顺序可以随便。
2、任何一个按钮都最多需要按下1次。因为按下第二次刚好抵消第一次,等于没有按。
这个问题可以转化成数学问题。 以3x3为例:
我们记L为待求解的原始布局矩阵。A(i , j)表示按下第i行第j列的按钮时的作用范围矩阵。
如:
L=
0 1 0
1 1 0
0 1 1
A(1 , 1)= A(2 , 2)=
1 1 0 0 1 0
1 0 0 1 1 1
0 0 0 0 1 0
每次按下一个按钮,可以转化成 原始矩阵 异或上 作用矩阵
假设x(i , j)表示:想要使得L回到全灭状态,第i行第j列的按钮是否需要按下。0表示不按,1表示按下。那么,这个游戏就转化为如下方程的求解:
L ^ x(1 , 1)*A(1 , 1) ^ x(1 , 2)*A(1 , 2) ^ x(1 , 3)*A(1 , 3) ^ x(2 , 1)*A(2 , 1) ^ ... ^ x(3 , 3)*A(3 , 3) = 0
其中x(i,j)是未知数。方程右边的0表示零矩阵,表示全灭的状态。直观的理解就是:原来的L状态,经过了若干个A(i,j)的变换,最终变成0:全灭状态。
两个矩阵异或等于 0 ,说明两个矩阵相等,所以上式可写为:
x(1 , 1)*A(1 , 1) ^ x(1 , 2)*A(1 , 2) ^ x(1 , 3)*A(1 , 3) ^ x(2 , 1)*A(2 , 1) ^ ... ^ x(3 , 3)*A(3 , 3) = L ,(懒的加括号了,异或是最晚算的)
两个矩阵相等,充要条件是矩阵中每个元素都相等,所以只要列出等式左右两边的矩阵上的每一个元素对应相等,
就可以将上述矩阵转化成了一个9元1次方程组:
简单地记做:AA * XX = LL ,最后解的:
x(1 , 1) x(1 , 2) x(1 , 3) 1 1 1
x(2 , 1) x(2 , 2) x(2 , 3) = 0 0 0
x(3 , 1) x(3 , 2) x(3 , 3) 0 0 1
也就是说,按下第一行的3个按钮,和右下角的按钮,就全灭了。
回到 题目的 5*6 矩阵,为了 表示方便,我们用 Xi 表示第 i 个按钮是否要按,Li 表示 L 矩阵的第 i 个元素
A(i , j)x: 第 i 行 第 j 列的按钮的作用矩阵 的 第 x 个元素
于是有:(注意 + 和 mod2 的组合 等效与于 ^ )
X1*A(1,1)1 + X2*A(1,2)1 + X3*A(1,3)1 +…………X30*A(5,6)1 = L1; mod 2
X1*A(1,1)2 + X2*A(1,2)2 + X3*A(1,3)2 +…………X30*A(5,6)2 = L2; mod 2
X1*A(1,1)3 + X2*A(1,2)3 + X3*A(1,3)3 +…………X30*A(5,6)3 = L3: mod 2
.
X1*A(1,1)30 + X2*A(1,2)30 + X3*A(1,3)30 +…………X30*A(5,6)30 = L30: mod 2
容易发现,第一行的 A(1,1)1, A(1,2)1,A(1,3)……A(5,6)1,合起来就是 A(1,1) 的全部元素,
这是因为 能够影响到当前开关的,当前开关也能影响到它,
这里影响到当前开关指的是:所有作用矩阵中,在当前开关位置为 1 的作用矩阵对应的开关
当前开关指的是也能影响到它指的是:当前开关对应的作用矩阵能作用于 影响到它的开关
所以,又有:
X1*A(1,1)1 + X2*A(1,1)2 + X3*A(1,1)3 +…………X30*A(1,1)30 = L1; mod 2
X1*A(1,2)1 + X2*A(1,2)2 + X3*A(1,2)3 +…………X30*A(1,2)30 = L2; mod 2
X1*A(1,3)1 + X2*A(1,3)2 + X3*A(1,3)3 +…………X30*A(1,3)30 = L3: mod 2
.
X1*A(5,6)1 + X2*A(5,6)2 + X3*A(5,6)3 +…………X30*A(5,6)30 = L30: mod 2
这就是我们要的增广矩阵。
Plus: 另外一种比较容易记住的看待这个问题的看法:
对于每一个开关,如果不知道其他开关的作用矩阵的话,他是与每一个开关都有影响的,影响它的变量是其他开关是否按下,
所以 影响一个开关的变量有30个,即有:
start ^ ( X1*a1 + X2*a2 + X3*a3 +…………X30*a30 )= end ;
其中,start 表示 当前开关的初始状态,end 表示当前开关的结束状态
Xi 表示:第 i 个开关是否按下,ai 表示 第 i 个开关按下后是否能影响 当前开关。
能够影响到当前开关的,当前开关也能影响到它(上面有解释),所以 ai,其实就是当前开关的作用矩阵。
上面式子可进一步化为:
X1*a1 + X2*a2 + X3*a3 +…………X30*a30 = end ^ start
综上:30 个开关的系数矩阵是 30*30
第 i 行,第 j 列的元素表示:第 j 个开关是否能够影响到 第 i 个开关,
1 表示 可,2 表示 非
代码:

#define _CRT_SECURE_NO_WARNINGS #include<stdio.h> #include<stdlib.h> #include<math.h> #define N 35 int a[N][N]; // 增广矩阵 int x[N]; // 未知数矩阵 void show(void) { puts(""); for (int i = 0; i < 30; i++) { for (int j = 0; j < 30 + 1; j++) { printf("%d ", a[i][j]); }puts(""); } } // 知道刚好唯一解才能这样写 void Gauss(void) { for (int i = 0; i < 30; i++) // 循环增广矩阵的 列 { if (a[i][i] == 0) // 如果该列的主元为 0 { for (int j = i + 1; j < 30; j++) // 循环主元一下的行 { if (a[j][i] != 0) { for (int k = i; k < 31; k++) { int t = a[j][k]; a[j][k] = a[i][k]; a[i][k] = t; } break; } } } // 化阶梯 for (int j = 0; j < 30; j++) // 循环行 { if (i != j&&a[j][i]) // 如果当前列,除了主元位置,还有的位置 不为 0 { for (int k = i; k < 31; k++) // 循环列 { // 两者等价 //a[j][k] = a[i][k] ^ a[j][k]; a[j][k] = (abs(a[j][k] + a[i][k])) % 2; } } } } for (int i = 0; i < 30; i++) x[i] = a[i][30]; } int main(void) { int t; scanf("%d", &t); for (int ii = 0; ii < t; ii++) { // 常数项向量 for (int i = 0; i < 30; i++) scanf("%d", &a[i][30]); // 系数矩阵 for (int i = 0; i < 30; i++) { /* 系数矩阵 的第 i 行,是根据 灯光的初始状态矩阵的第 i 个元素 列出来 这里将对应的第 i 个元素 化为 灯光的初始状态矩阵的 行列坐标*/ int x0 = i / 6, y0 = i % 6; for (int j = 0; j < 30; j++) { /* 系数矩阵 的每一列 代表 灯光的初始状态矩阵的全部元素 这里将对应的第 i 行 第 j 个元素 化为 灯光的初始状态矩阵的 行列坐标*/ int x = j / 6, y = j % 6; if (abs(x - x0) + abs(y - y0) <= 1) // 包括 自己和上下左右,如果有的话 a[i][j] = 1; else a[i][j] = 0; } } // show(); Gauss(); printf("PUZZLE #%d ", ii + 1); for (int i = 0; i < 30; i++) { if ((i + 1) % 6 == 0) printf("%d ", x[i]); else printf("%d ", x[i]); } } system("pause"); return 0; }
Flip Game
- Choose any one of the 16 pieces.
- Flip the chosen piece and also all adjacent pieces to the left, to the right, to the top, and to the bottom of the chosen piece (if there are any).
 Consider the following position as an example:
Consider the following position as an example:
bwbw
wwww
bbwb
bwwb
Here "b" denotes pieces lying their black side up and "w" denotes pieces lying their white side up. If we choose to flip the 1st piece from the 3rd row (this choice is shown at the picture), then the field will become:
bwbw
bwww
wwwb
wwwb
The goal of the game is to flip either all pieces white side up or all pieces black side up. You are to write a program that will search for the minimum number of rounds needed to achieve this goal.
题解:该题的思路与上面那题 类似,不过多了一步,要枚举自由变元,判断哪种解法最快。
怎么枚举呢?
一个自由变元有 0,1 两种情况,所以 num 个自由变元有 2^num 种情况。
我们用 i 从0 循环到 2^num , 每一个 i 的二进制对应 对应 1 种情况
如:i = 1 , num = 4,则 i 的二进制为 0001, 则对应的四个自由变元的值 可分别设为 0,0,0,1,
此时,方程唯一可解,然后记录此时需要翻动的次数,然后通过比较得到最优解。
这里再讲一下,之前没涉及到的,int数组 f[N]; 用来记录自由变元的行数
f[i]:第 i 个自由变元的列数,同时也是行数
记录的两种方法:
① 行阶梯矩阵的同一行全为 0
int num = 0;
if (a[k][col] == 0)
{
k--;
f[num++] = col;
continue;
}
② 无穷解,无法求解的变元
int cnt = 0;
for (int i = 0; i < COL; i++)
if (free_x[i])
f[cnt++] = i;
代码:

#define _CRT_SECURE_NO_WARNINGS #include<stdio.h> #include<stdlib.h> #include<string.h> #include<math.h> #define inf 0x3f3f3f3f #define N 35 char str[N][N]; int a[N][N]; int x[N]; int free_x[N]; int f[N]; // 记录自由变元的行数 int ROW, COL; void show(void) { puts(""); for (int i = 0; i < ROW; i++) { for (int j = 0; j < COL + 1; j++) { printf("%d ", a[i][j]); }puts(""); } } void init() { memset(a, 0, sizeof(a)); for (int i = 0; i < 16; i++) { int x0 = i / 4, y0 = i % 4; for (int j = 0; j < 16; j++) { int x = j / 4, y = j % 4; if (abs(x0 - x) + abs(y0 - y) <= 1) a[i][j] = 1; } } } // 0 1 方程组下的高斯消元 int Gauss(void) { memset(free_x, 1, sizeof(free_x)); memset(x, 0, sizeof(x)); int k = 0, col = 0; int num = 0; for (; k < ROW&&col < COL; k++, col++) { int max_r = k; for (int i = k + 1; i < ROW; i++) if (abs(a[i][col]) > abs(a[max_r][col])) max_r = i; if (max_r != k) for (int i = 0; i < COL + 1; i++) { int t = a[max_r][i]; a[max_r][i] = a[k][i]; a[k][i] = t; } if (a[k][col] == 0) { k--; f[num++] = col; continue; } for (int i = k + 1; i < ROW; i++) { if (a[i][col] != 0) for (int j = col; j < COL + 1; j++) { a[i][j] = a[i][j] ^ a[k][j]; // a[i][j] = (a[i][j] - a[k][j] + 2) % 2; } } } for (int i = k; i < ROW; i++) { if (a[i][COL] != 0) return -1; } if (k < COL) { return COL - k; } for (int i = k - 1; i >= 0; i--) { int t = a[i][COL]; for (int j = i + 1; j < COL; j++) { if (a[i][j] != 0) { t = t ^ (a[i][j] * x[j]); // t = (t - x[i][j] * x[j] + 2) % 2 } } x[i] = t / a[i][i] % 2; } return 0; } int fun() { int num = Gauss(); if (num == -1) // 无解 return inf; else if (num == 0) // 唯一解 { int sum = 0; for (int i = 0; i < COL; i++) sum += x[i]; return sum; } else // 有无穷解,枚举变元 { /*// 一个自由变元有 0,1 两种情况,所以 num 个自由变元有 2^num 种情况, 每一个 i 的二进制对应 对应 1 种情况 如:i = 1 , num = 4,则 i 的二进制为 0001, 则对应的四个自由变元的值 可分别设为 0,0,0,1 */ int ans = inf; for (int i = 0; i < (1 << num); i++) { int cnt = 0; // 记录自由变元中 1 的个数 for (int j = 0; j < num; j++) { if (i&(1 << j)) // 如果 i 的第 j 位为 1 { x[f[j]] = 1; cnt++; } else x[f[j]] = 0; } // 给自由变元赋值后,方程即唯一可解,与上面的唯一解解法相同 for (int j = COL - num - 1; j >= 0; j--) { x[j] = a[j][COL]; // 将该行的系数矩阵的元素全都异或起来,就等于 该行的常数项,即方程的解 for (int k = j + 1; k < COL; k++) { if (a[j][k]) x[j] = x[j] ^ x[k]; } cnt += x[j]; } ans = ans > cnt ? cnt : ans; } return ans; } } int main(void) { ROW = COL = 16; for (int i = 0; i < 4; i++) scanf("%s", str[i]); init(); // 初始化 系数矩阵 for (int i = 0; i < 16; i++) { if (str[i / 4][i % 4] == 'b') a[i][16] = 1; //初始化 常数项向量 else a[i][16] = 0; } // show(); int a1 = fun(); init(); for (int i = 0; i < 16; i++) { if (str[i / 4][i % 4] == 'w') a[i][16] = 1; else a[i][16] = 0; } int a2 = fun(); if (a1 == inf && a2 == inf) printf("Impossible "); else printf("%d ", a1 > a2 ? a2 : a1); system("pause"); return 0; }
例题:
开关问题
每组测试数据的格式如下:
第一行 一个数N(0 < N < 29)
第二行 N个0或者1的数,表示开始时N个开关状态。
第三行 N个0或者1的数,表示操作结束后N个开关的状态。
接下来 每行两个数I J,表示如果操作第 I 个开关,第J个开关的状态也会变化。每组数据以 0 0 结束。
题解:
上面两个的结合。
代码:

#define _CRT_SECURE_NO_WARNINGS #include<stdio.h> #include<stdlib.h> #include<string.h> #include<math.h> #define mem(a,b) memset(a,b,sizeof(a)) #define N 105 int a[N][N]; int x[N]; // 解集 bool free_x[N]; // 判断是否是不确定的变元 int free_num; int ROW, COL; // 行数,列数 void show(void) { puts(""); for (int i = 0; i < ROW; i++) { for (int j = 0; j < COL + 1; j++) { printf("%d ", a[i][j]); }puts(""); } } inline int gcd(int a, int b) { return b ? gcd(b, a%b) : a; } inline int lcm(int a, int b) { return a*b / gcd(a, b); } // 只需要判段有无解,和自由变元的个数 int Gauss(void) { int row = 0, col = 0; for (; row < ROW&&col < COL; row++, col++) { int max_r = row; for (int i = row + 1; i < ROW; i++) if (abs(a[i][col]) > abs(a[max_r][col])) max_r = i; if (max_r != row) for (int i = row; i < COL + 1; i++) { int t = a[row][i]; a[row][i] = a[max_r][i]; a[max_r][i] = t; } if (a[row][col] == 0) { row--; continue; } for (int i = row + 1; i < ROW; i++) { if (a[i][col] != 0) { int LCM = lcm(abs(a[i][col]), abs(a[row][col])); int ta = LCM / abs(a[i][col]); int tb = LCM / abs(a[row][col]); if (a[i][col] * a[row][col] < 0) tb = -tb; for (int j = col; j < COL + 1; j++) { a[i][j] = a[i][j] * ta - a[row][j] * tb; } } } } //show(); //无解:化简的增广阵中存在(0,0,...,a)这样的行,且a!=0 for (int i = row; i < ROW; i++) if (a[i][col] != 0) return -1; return COL - row; } int start[N];//开始状态 int end[N];//结束状态 int main(void) { int t;scanf("%d", &t); while (t--) { int n; scanf("%d", &n); for (int i = 0; i < n; i++) //开始状态 scanf("%d", &start[i]); for (int i = 0; i < n; i++) //最终状态 scanf("%d", &end[i]); mem(a, 0); for (int i = 0; i < n; i++) //每个方程的解 a[i][n] = start[i] ^ end[i]; for (int i = 0; i < n; i++) //第i个开关受第i个开关影响 a[i][i] = 1; int t1, t2; while (scanf("%d%d", &t1, &t2) != EOF && (t1 + t2)) { a[t2 - 1][t1 - 1] = 1; // 第 t1 个开关 影响 第 t2 个开关 } show(); ROW = COL = n; free_num = Gauss(); if (free_num == -1) printf("Oh,it's impossible~!! "); else printf("%d ", 1 << free_num); // free_num 个自由变元 有 2^free_num 种方法 } system("pause"); return 0; }
例题:
SETI
For some years, quite a lot of work has been put into listening to electromagnetic radio signals received from space, in order to understand what civilizations in distant galaxies might be trying to tell us. One signal source that has been of particular interest to the scientists at Universit´e de Technologie Spatiale is the Nebula Stupidicus.
Recently, it was discovered that if each message is assumed to be transmitted as a sequence of integers a0, a1, ...an-1 the function f (k) = ∑0<=i<=n-1aiki (mod p) always evaluates to values 0 <= f (k) <= 26 for 1 <= k <= n, provided that the correct value of p is used. n is of course the length of the transmitted message, and the ai denote integers such that 0 <= ai < p. p is a prime number that is guaranteed to be larger than n as well as larger than 26. It is, however, known to never exceed 30 000.
These relationships altogether have been considered too peculiar for being pure coincidences, which calls for further investigation.
The linguists at the faculty of Langues et Cultures Extraterrestres transcribe these messages to strings in the English alphabet to make the messages easier to handle while trying to interpret their meanings. The transcription procedure simply assigns the letters a..z to the values 1..26 that f (k) might evaluate to, such that 1 = a, 2 = b etc. The value 0 is transcribed to '*' (an asterisk). While transcribing messages, the linguists simply loop from k = 1 to n, and append the character corresponding to the value of f (k) at the end of the string.
The backward transcription procedure, has however, turned out to be too complex for the linguists to handle by themselves. You are therefore assigned the task of writing a program that converts a set of strings to their corresponding Extra Terrestial number sequences.
模运算下的高斯消元,入门题
题解:
输入一个素数p和一个字符串s(只包含小写字母和‘*’),字符串中每个字符对应一个数字,'*'对应0,‘a’对应1,‘b’对应2....
例如str[] = "abc", 那么说明 n=3, 字符串所对应的数列为1, 2, 3。
题目中定义了一个函数:
a0*1^0 + a1*1^1+a2*1^2+........+an-1*1^(n-1) = f(1)(mod p), f(1) = str[0] = a = 1;
a0*2^0 + a1*2^1+a2*2^2+........+an-1*2^(n-1) = f(2)(mod p), f(2) = str[1] = b = 2;
..........
a0*n^0 + a1*n^1+a2*n^2+........+an-1*n^(n-1) = f(n)(mod p),f(n) = str[n-1] = ````
求出 a0,a1,a2....an-1.
思路:若字符串长度为n,那么这是一个含有n个方程n个未知数的线性方程组,所以只需把相应的系数转为成矩阵解方程组。高斯消元+同余方程。
代码:

#define _CRT_SECURE_NO_WARNINGS #include<stdio.h> #include<stdlib.h> #include<string.h> #include<math.h> #define N 100 int p, COL, ROW; char s[N]; int a[N][N]; int x[N]; inline int gcd(int a, int b) { return b ? gcd(b, a%b) : a; } inline int lcm(int a,int b) { return a*b / gcd(a, b); } int qmul(int a, int b, int c) { int res = 1; while (b) { if (b & 1) res = res*a%c; b >>= 1; a = (a%c)*(a%c) % c; } return res; } int Gauss() { int k, col; for (k = 0, col = 0; k < ROW&&col < COL; k++, col++) { int max_r = k; for (int i = k + 1; i < ROW; i++) { if (abs(a[i][col]) > abs(a[max_r][col])) max_r = i; } if (max_r != k) { for (int i = col; i < COL + 1; i++) { int t = a[max_r][i]; a[max_r][i] = a[k][i]; a[k][i] = t; } } if (a[k][col] == 0) { k--; continue; } for (int i = k + 1; i < ROW; i++) { if (a[i][col] != 0) { int LCM = lcm(abs(a[i][col]), abs(a[k][col])); int ta = LCM / a[i][col], tb = LCM / abs(a[k][col]); if (a[i][col] * a[k][col] < 0) tb = -tb; for (int j = col; j < COL + 1; j++) a[i][j] = ((a[i][j] * ta - a[k][j] * tb) % p + p) % p; } } } for (int i = k; i < ROW; i++) { if (a[i][col] != 0) return 0; } if (k < COL) return COL - k; for (int i = COL - 1; i >= 0; i--) { int t = a[i][COL]; for (int j = i + 1; j < COL; j++) t = (t - a[i][j] * x[j] % p + p) % p; // 不让整除的变成 0 //while (t%a[i][i] != 0) // t += p; //x[i] = (t / a[i][i]) % p; // 乘法逆元? x[i] = (t * qmul(a[i][i], p - 2, p)) % p; } return 0; } int main(void) { int t; scanf("%d", &t); while (t--) { scanf("%d %s", &p, s); COL = ROW = strlen(s); for (int i = 0; i < ROW; i++) { if (s[i] == '*') a[i][COL] = 0; else a[i][COL] = s[i] - 'a' + 1; for (int j = 0; j < COL; j++) a[i][j] = qmul(i + 1, j, p); } Gauss(); for (int i = 0; i < COL; i++) printf("%d ", x[i]); puts(""); } system("pause"); return 0; }
============ =========== ========= ======== ======== ====== ====== ==== == =
宿新市徐公店 宋代: 杨万里
儿童急走追黄蝶,
