Markov's Inequality
中文叫马尔科夫不等式或马尔可夫不等式。
若随机变量(X)只取非负值,则(forall a>0),有
[mathbb{P} (Xge a) le dfrac{mathbb{E}(X)}{a}
]
证明:
取(Y_a=amathbb{I}(Xge a)),则必有(Y_ale X),进而有(mathbb{E}(Y_a)le mathbb{E}(X))。
而
[egin{aligned}
mathbb{E}(Y_a)&=acdotmathbb{P} (Xge a)+0cdotmathbb{P} (X< a)\
&=acdotmathbb{P} (Xge a)
end{aligned}
]
因此有(amathbb{P}le mathbb{E}(X)),得证。
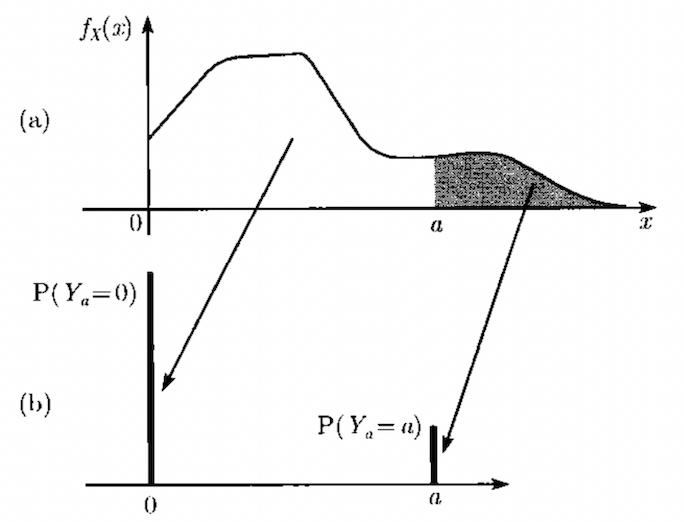
以上证明非常简单,如果想直观地理解一下,就是将整个(X)的分布减小(分布图像向左移)到(0)和(a)处两个部分,减小后的分布的期望一定小于原来的期望。如下图:
如果直接用积分形式来证,也非常直接:
[egin{aligned}
mathbb{E}(X)&=int_{-infty}^{infty}xf(x)dx\
&geint_{a}^{infty}xf(x)dx quad (age 0)\
&geint_{a}^{infty}af(x)dx\
&=a int_{a}^{infty}f(x)dx\
&=a mathbb{P} (Xge a)
end{aligned}
]
Markov's inequality用得非常少,因为它给出的上界宽松了,但用它可以证明另一个著名的不等式——Chebyshev's inequality,中文叫切比雪夫不等式。
Chebyshev's Inequality
假设随机变量(X)有均值(mu)、方差(sigma^2),则(forall c>0),有:
[mathbb{P} (vert X-muvert ge c) le dfrac{sigma^2}{c^2}
]
证明:
取(Y=(X-mu)^2),则它非负,而(c^2)也非负,使用Markov's Inequality,有:
[mathbb{P} (Yge c^2) le dfrac{mathbb{E}(Y)}{c^2}
]
而(mathbb{E}(Y)=mathbb{E}[(X-mu)^2]=sigma^2),(Yge c^2)与(vert X-muvert ge c)又是等价的,因此得证。