二叉堆
概念
二叉堆本质上是一种完全二叉树,它分为两个类型。最大堆以及最小堆,二叉堆的根节点叫作堆顶。最大堆和最小堆的特点决定了:最大堆的堆顶是整个堆中的最大元素;最小堆的堆顶是整个堆中的最小元素
最大堆与最小堆
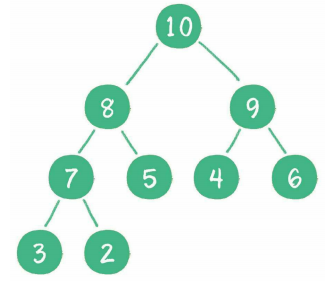
1. 最大堆
最大堆的任何一个父节点的值,都大于或等于它左、右孩子节点的值。
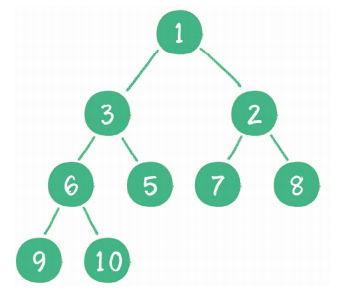
2. 最小堆
最小堆的任何一个父节点的值,都小于或等于它左、右孩子节点的值。
二叉堆自我调整
1. 插入节点
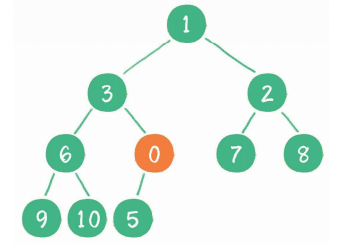
当二叉堆插入节点时,插入位置是完全二叉树的最后一个位置。例如插入一个新节点,值是 0。

这时,新节点的父节点5比0大,显然不符合最小堆的性质。于是让新节点“上浮”,和父节点交换位置。
继续用节点0和父节点3做比较,因为0小于3,则让新节点继续“上浮”。
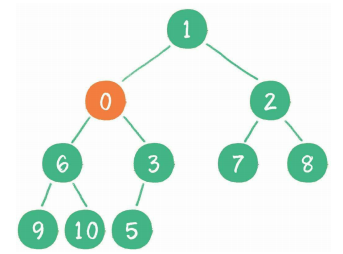
继续比较,最终新节点0“上浮”到了堆顶位置。
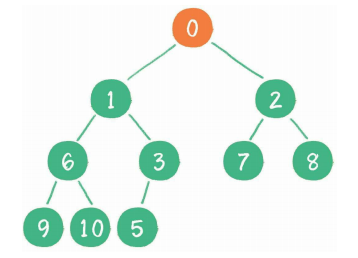
2. 删除节点
二叉堆删除节点的过程和插入节点的过程正好相反,所删除的是处于堆顶的节点。例如删除最小堆的堆顶节点1。
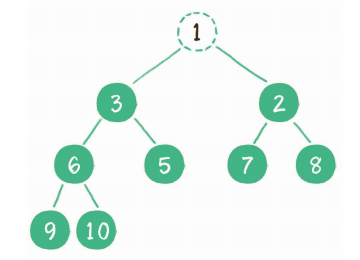
这时,为了继续维持完全二叉树的结构,我们把堆的最后一个节点10临时补到原本堆顶的位置。
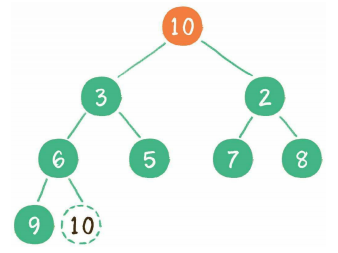
接下来,让暂处堆顶位置的节点10和它的左、右孩子进行比较,如果左、右孩子节点中最小的一个(显然是节点2)比节点10小,那么让节点10“下沉”。
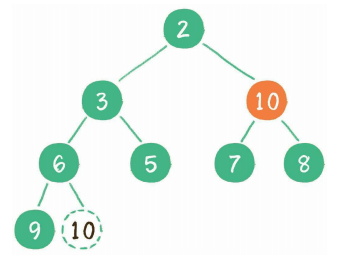
继续让节点10和它的左、右孩子做比较,左、右孩子中最小的是节点7,由于10大于7,让节点10继续“下沉”。

3. 构建二叉堆
构建二叉堆,也就是把一个无序的完全二叉树调整为二叉堆,本质就是让所有非叶子节点依次“下沉”。下面举一个无序完全二叉树的例子,如下图所示。
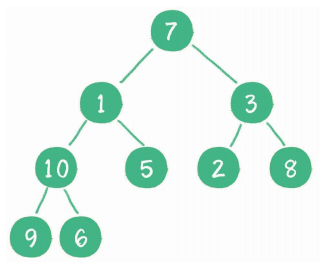
首先,从最后一个非叶子节点开始,也就是从节点10开始。如果节点10大于它左、右孩子节点中最小的一个,则节点10“下沉”。
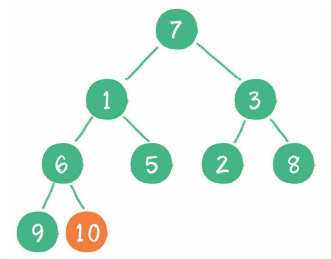
接下来轮到节点3,如果节点3大于它左、右孩子节点中最小的一个,则节点3“下沉”。
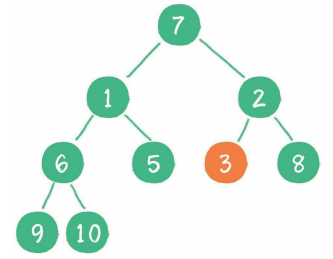
然后轮到节点1,如果节点1大于它左、右孩子节点中最小的一个,则节点1“下沉”。事实上节点1小于它的左、右孩子,所以不用改变。接下来轮到节点7,如果节点7大于它左、右孩子节点中最小的一个,则节点7“下沉”。
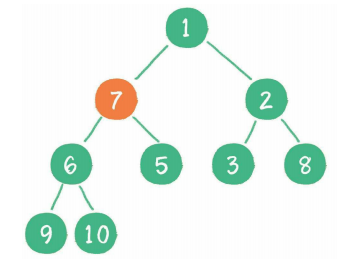
节点7继续比较,继续“下沉”。

如何实现一个堆?
完全二叉树比较适合用数组来存储。用数组来存储完全二叉树是非常节省存储空间的。因为我们不需要存储左右子节点的指针,单纯地通过数组的下标,就可以找到一个节点的左右子节点和父节点。
如图所示:
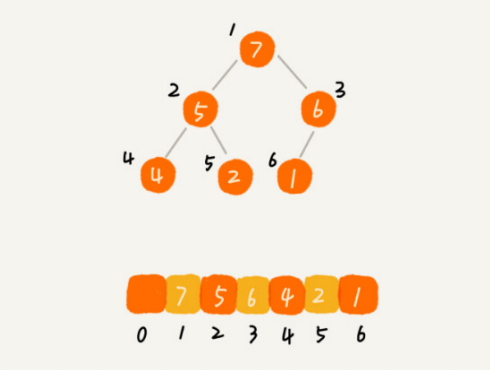
从图中我们可以看到,数组中下标为i的节点的左子节点,就是下标为2*i的节点,右子节点就是下标为2*i+1的节点,父节点就是下标为i/2的节点。
1. 往堆中插入一个元素
往堆中插入一个元素后,需要进行调整,让其重新满足堆的特性,这个过程我们起了一个名字,就叫作堆化(heapify)。堆化实际上有两种,从下往上和从上往下。
例如对于如下二叉堆,添加元素22:
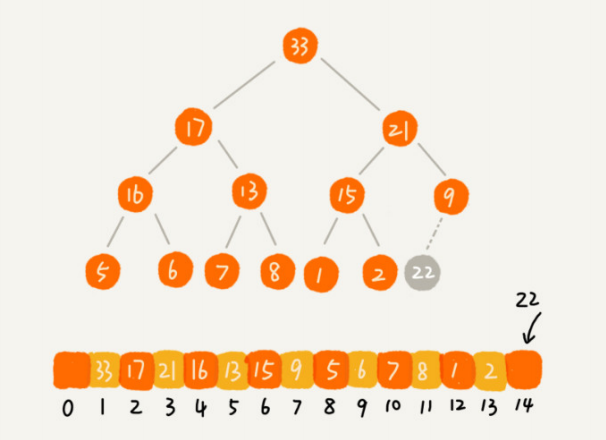

代码示例:
package arithmetic.com.ty.binary; public class Heap { private int[] a; // 数组,从下标 1 开始存储数据 private int n; // 堆可以存储的最大数据个数 private int count; // 堆中已经存储的数据个数 public Heap(int capacity) { a = new int[capacity + 1]; n = capacity; count = 0; } public void insert(int data) { if (count >= n) { return; // 堆满了 } ++count; a[count] = data; int i = count; // i/2是其父节点的位置,当比父节点值大的时候,进行交换 // 自下往上堆化 while (i / 2 > 0 && a[i] > a[i / 2]) { // swap() 函数作用:交换下标为 i 和 i/2 的两个元素 int temp = a[i/2]; a[i/2] = a[i]; a[i] = temp; //继续比较其父节点 i = i / 2; } } }
2. 删除堆顶元素
假设我们构造的是大顶堆,堆顶元素就是最大的元素。当我们删除堆顶元素之后,就需要把第二大的元素放到堆顶,那第二大元素肯定会出现在左右子节点中。然后我们再迭代地删除第二大节点,以此类推,直到叶子节点被删除。不过这种方法有点问题,就是
最后堆化出来的堆并不满足完全二叉树的特性。
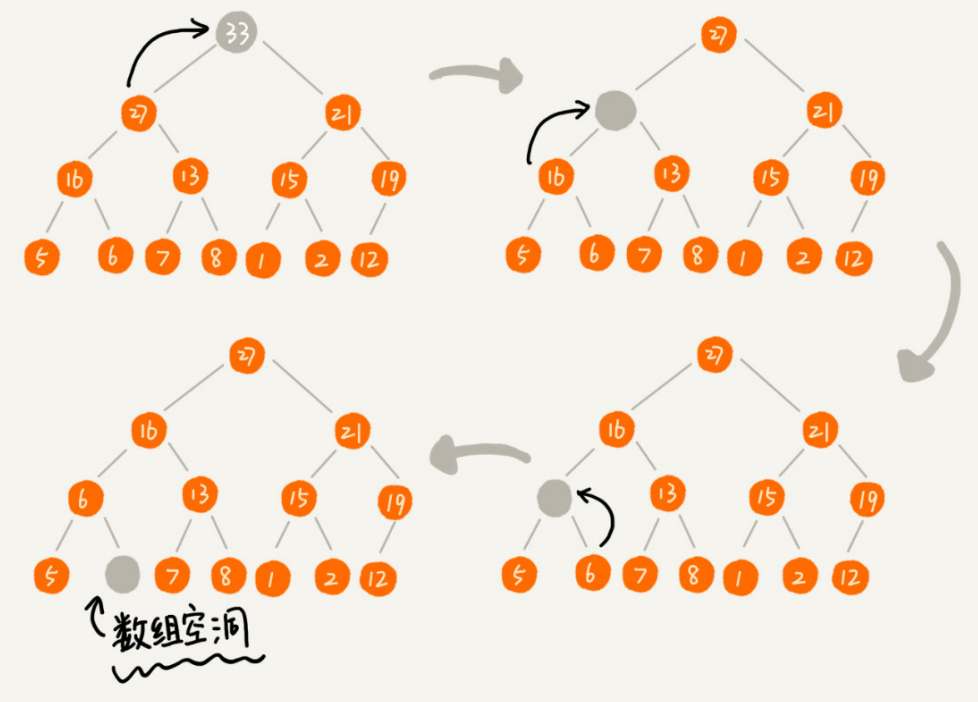
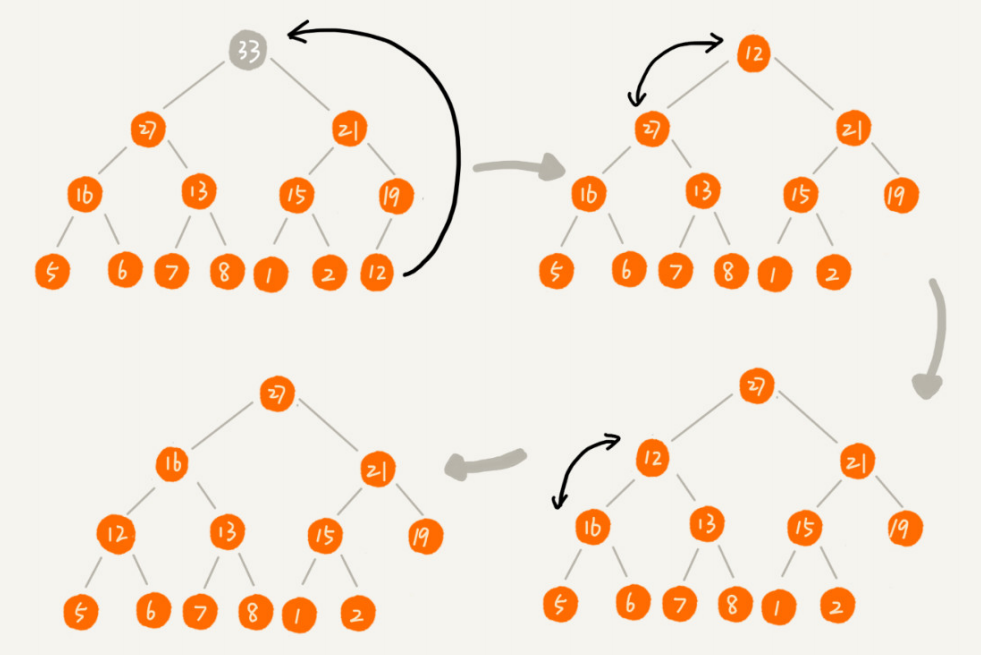
实际上,我们稍微改变一下思路,就可以解决这个问题。你看我画的下面这幅图。我们把最后一个节点放到堆顶,然后利用同样的父子节点对比方法。对于不满足父子节点大小关系的,互换两个节点,并且重复进行这个过程,直到父子节点之间满足大小关系为止。这就是从上往下的堆化方法。因为我们移除的是数组中的最后一个元素,而在堆化的过程中,都是交换操作,不会出现数组中的“空洞”,所以这种方法堆化之后的结果,肯定满足完全二叉树的特性。
代码示例:
public void removeMax() { if (count == 0) { // 堆中没有数据 return; } //将二叉堆最后一个元素设置到堆顶 a[1] = a[count]; --count; heapify(a, count, 1); } private void heapify(int[] a, int n, int i) { // 自上往下堆化 while (true) { int maxPos = i; //如果左子节点大于堆顶的值,最大位置设为左节点 if (i * 2 <= n && a[i] < a[i * 2]) { maxPos = i * 2; } //右子节点有可能比左子节点大,因此继续比较 if (i * 2 + 1 <= n && a[maxPos] < a[i * 2 + 1]) { maxPos = i * 2 + 1; } //以上两步就是将父节点与左右子节点进行比较,得到最大数值的位置。如果位置没变化,直接退出循环,结束流程 if (maxPos == i) { break; } int temp = a[i]; a[i] = a[maxPos]; a[maxPos] = temp; i = maxPos; } }