题面:

分析:既然是求期望,总的方案数为 (n^2) ,求出来的期望又要乘一个 (n^2) ,则题意可简化为(sum_i^nsum_j^n w[i][j]) ,其中定义 (w[i][j]) 表示在连接 (i,j) 的链中出现过的不重复的黑恶势力数,再定义 (d(i,j)) 表示连接 (i,j) 的链。
为了简化题目,我们认为这个图为一棵树(本来就是),任意找个点为根,而将黑恶势力认为是每条边上的颜色。那么显而易见,这棵树满足每个节点有且仅有一条父边(废话),并且每条边都只有一种颜色而不是五颜六色的($By $ (XZY) 巨佬所以不是废话),即每个点唯一对应一种颜色,不妨假设每个点的颜色为它父边的颜色。
根据这个性质,我们可以很快有一个初步的容斥想法。考虑这么一张图。
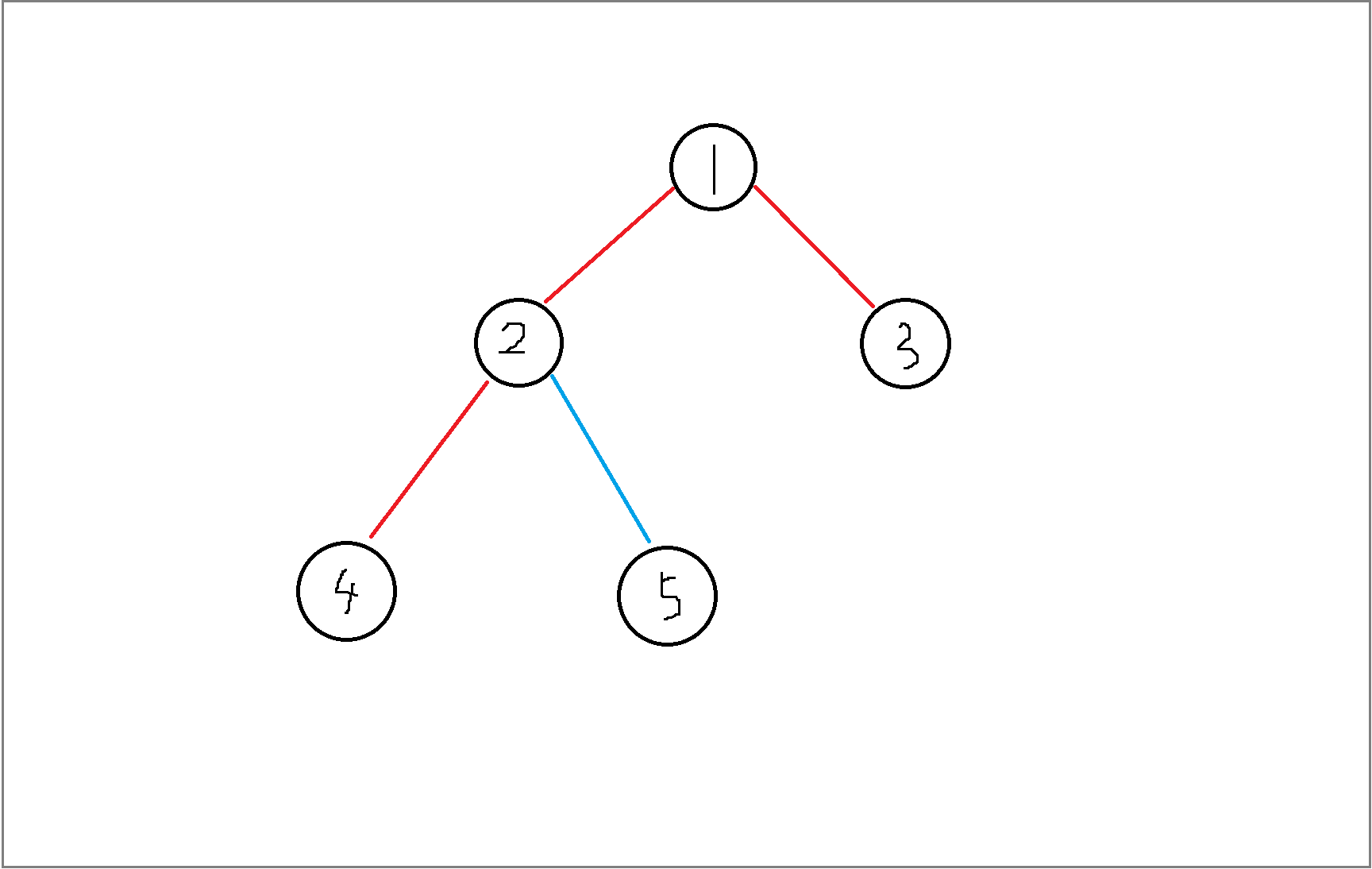
对于整张图我们难以操作判断贡献,但如果我们以一种固定的颜色 (A) ,把这种颜色的边全部断开,那么这棵树就会变成多个不相联通的块,而对于每一个块,块内所有颜色为(A)的边都没有贡献。换句话说,对于这个块来说,颜色(A)是没有贡献的。
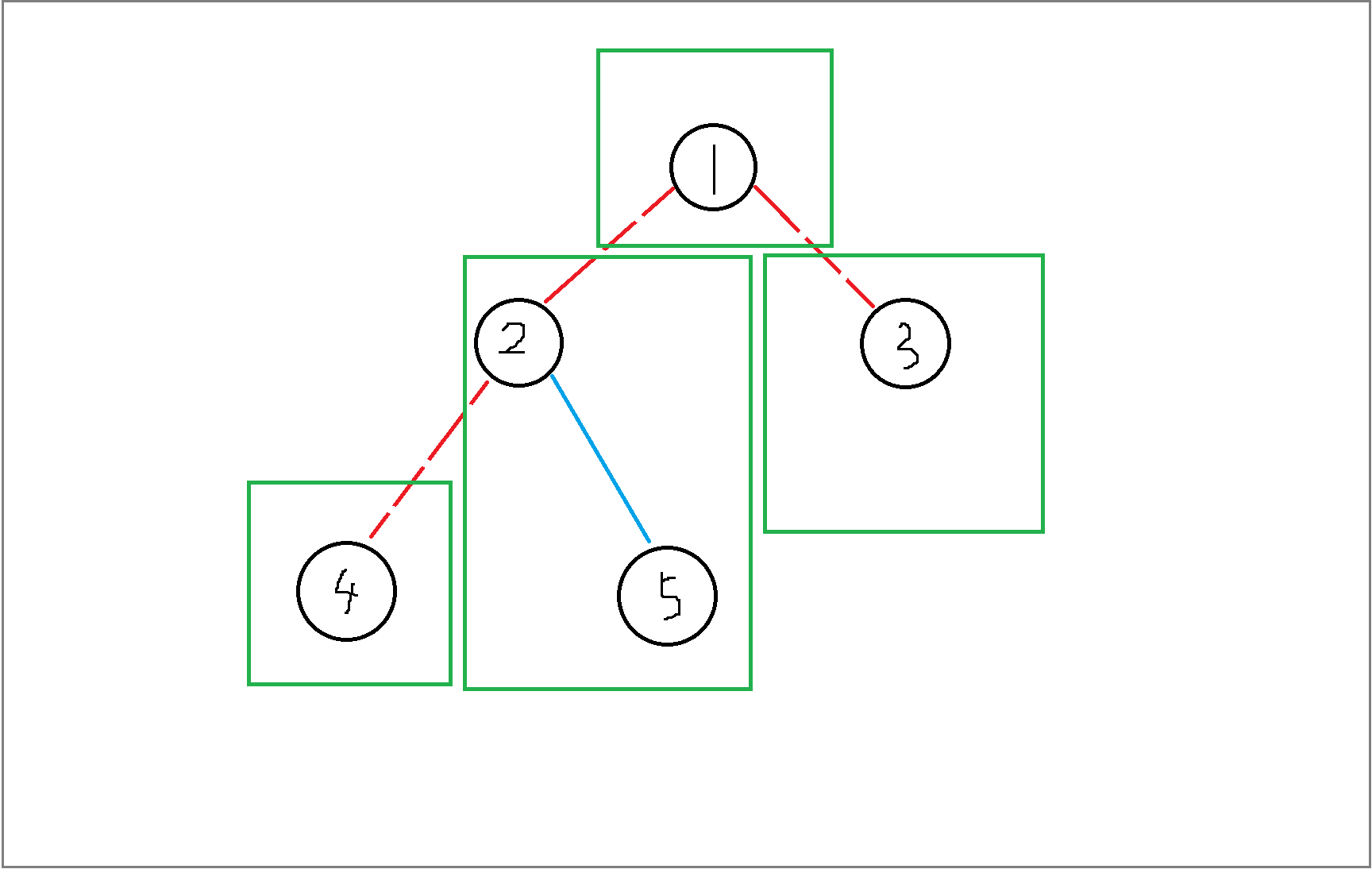
即上图,对于每个绿色的块 (S) 内,(中出现了红色边sum^{S.card}_i sum^{S.card}_j [d(i,j)中出现了红色边]=0)。
(从这行以下请感性理解或自觉 (Mod) (XZY) (or) (LX) (or) (HL) (or) (CXR) (or) (LWY)。)
(Sol):我们实际上只需要统计这个颜色 (A) 在整棵树里可能带来的所有影响(即 (n^2) ,它至多存在于 (n^2) 条链中),减去各个块内的链数(即 (S.card^2) ,它在这个块里的所有链上都没有贡献),就是这种颜色所带来的总的贡献。
考虑怎么求这个贡献。
由于我们已经知道了每个点对应且仅对应一种颜色,即上文说过的这个点父边的颜色,那么我们就可以暴力 (dfs) 。对于当前这个节点 (i) 所对应的颜色 (col[i]) 操作即可。
维护一个 (top[i]) 表示这个节点 (i) 所对应的颜色 (col[i]) 在 (dfs) 的过程中上一次出现的位置。如上图,(top[2]=1) ,(top[3]=1) ,(top[4]=2) ;特别的,如果这个颜色是第一次出现,那么它的 (top[i]) 将会被设为 (0) 。如上图,(top[1]=0) ,(top[5]=0) 。
在这种时候就需要一个 (lst) 辅助数组滚动记录,不过这不是重点。
接下来就是求这些连通块内的大小。显而易见的,每个以 (i) 为深度最小的节点的连通块大小就是 (f[i]=size[top[i]]-sum _{j in {x|top[x]=i}}size[j]) ,其中 (size[u]) 表示 (u) 的子树大小 。通俗一点的解释就是下图。
.png)
我把绿的改成紫的了,仅此而已。
但是这就很容易能得到:每个以 (i) 为最小深度的连通块的大小,就是这个 (i) 的子树大小,减掉所有以它为端点的向下延伸的链中,第一次碰到的相同颜色的节点的子树大小。注意,是对于每条链而言的第一次碰到的相同颜色。如上图,节点 (2) 所对应的连通块大小就是 (size[2]-size[4]) ,因为节点 (4) 在 (2) 的子树中,且与 (2) 的颜色相同,且是 (d(2,4)) 上除 (2) 外第一个同为红色的点;节点 (3) 所对应的连通块大小就是 (size[3]) ,因为它是一个叶子节点。
很明显,(ans=sum_i^n (n^2-f[i]^2-rtc[i])=n^3-sum_i^n (f[i]^2+rtc[i])) ,意义就是每种颜色(共 (n) 种,所以是 (n*n^2=n^3))的贡献除去这种颜色的无用贡献(本来应该对于每种颜色单独计算,但发现答案不互斥,直接求和),至于 (rtc[i]) 将在下面提到。
有些小细节要注意。首先是如果不新开一层 (f[i]) ,而是直接修改 (size[i]) ,要按 (dfs) 序进行子树的加减操作,而不能在树上直接进行(比如 (std) )。因为可能会出现先把子节点减掉再减父节点的事情。
然后是这回的数据有了一层限制(或者说题目忘记说了?),就是 (dfs) 序就是 ([1,n]) 的顺序排列。这导致了可以少打一下求 (dfs) 序的循环。
最后是关于每种颜色的在整棵树里第一次出现的问题 ,我们需要用一个 (rtc[i]) 存储,初始化为 (n) ,每次搜到 (col[j]=n) (&) (!top[j]) 的节点 (j) 就需要 (rtc[i]-=size[j]) 。想想为什么。
然后就 (A) 了。
(Code):
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=500035;
const int maxm=1000035;
struct Edge
{
int v,w;
Edge(int a=0,int b=0):v(a),w(b) {}
}edges[maxm];
int n;
int size[maxn],rtc[maxn],top[maxn],lst[maxn];
int edgeTot,head[maxn],nxt[maxm];
ll ans;
int read(){
char ch=getchar();
int num=0,fl=1;
for(;!isdigit(ch);ch=getchar())if(ch=='-') fl=-1;
for(;isdigit(ch);ch=getchar())num=(num<<1)+(num<<3)+ch-48;
return num*fl;
}
void addedge(int u,int v,int w)
{
edges[++edgeTot]=Edge(v,w),nxt[edgeTot]=head[u],head[u]=edgeTot;
edges[++edgeTot]=Edge(u,w),nxt[edgeTot]=head[v],head[v]=edgeTot;
}
void dfs(int x,int fa)
{
size[x]=1;
for(int i=head[x];i!=-1;i=nxt[i])
{
int v=edges[i].v,w=edges[i].w;
if(v==fa) continue;
top[v]=lst[w],lst[w]=v;
dfs(v,x),size[x] += size[v];
lst[w]=top[v];//,size[top[v]] -= size[v];
if(!top[v]) rtc[w] -= size[v];
}
}
int main()
{
// freopen("forest.in","r",stdin);
// freopen("forest.out","w",stdout);
memset(head,-1,sizeof head);
n=read();
for(int i=1,u,v,w;i<n;i++)
u=read(),v=read(),w=read(),addedge(u,v,w);
for(int i=1;i<=n;i++)rtc[i]=n;
ans=1ll*n*n*n;
dfs(1,0);
for(int i=1;i<=n;i++)
if(top[i])size[top[i]]-=size[i];
for(int i=1;i<=n;i++)
{
if(i!=1)ans-=1ll*size[i]*size[i];
ans-=1ll*rtc[i]*rtc[i];
}
printf("%lld
",ans);
return 0;
}