参考链接:
1.https://blog.csdn.net/TaiJi1985/article/details/75087742
2.李航《统计学习方法》7.1节 线性可分支持向量机与硬间隔最大化
3.https://zhuanlan.zhihu.com/p/45444502,第三部分 手推SVM
本文目标:理解SVM的原始目标,即间隔最大化,并将其表示为约束最优化问题的转换道理。
背景知识:假设已经知道了分离平面的参数w和b,函数间隔γ',几何间隔γ,不懂的可以参考书本及其它。
为了将线性可分的数据集彻底分开,并分得最好,SVM的原始目标是找到一个平面(用w,b表示,二维数据中是一条直线,如下图所示),使得该平面与正负两类样本的最近样本点的距离最大化。简单的说,就是任给一个平面w,b,总有一个样本点离它的距离最近(点到平面的距离,可以用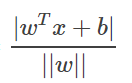 来表示),过该样本点作平行于分割平面的平面,两个平面形成分隔带。我们的目标是比较各种平面(无数个),找出一个平面使得“分隔带最胖”。那么如何来表述“分隔带最胖”呢?
来表示),过该样本点作平行于分割平面的平面,两个平面形成分隔带。我们的目标是比较各种平面(无数个),找出一个平面使得“分隔带最胖”。那么如何来表述“分隔带最胖”呢?
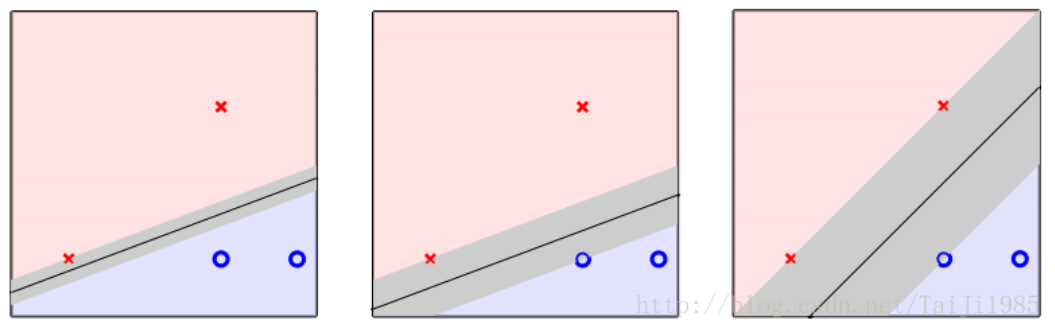 (引自参考链接1)
(引自参考链接1)
对于平面w,b来说,假设距离平面最近的点是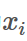 ,又由于该平面w,b可以将所有样本点正确分类,即满足
,又由于该平面w,b可以将所有样本点正确分类,即满足![]() ,因此我们可以将上述最近点
,因此我们可以将上述最近点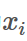 到平面w,b的距离改写为
到平面w,b的距离改写为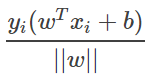 ,其中
,其中 取值为+1或-1。因此我们的目标就是最大化
取值为+1或-1。因此我们的目标就是最大化 ,注意该式子中
,注意该式子中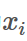 已经是离超平面w,b最近点了,称为γ超平面w,b关于训练数据集T的几何间隔。
已经是离超平面w,b最近点了,称为γ超平面w,b关于训练数据集T的几何间隔。
因此我们的原始问题:求得一个几何间隔最大的分离超平面,可以表示为下述约束最优化问题:
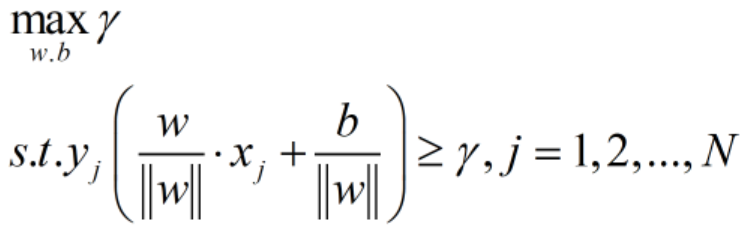
重要问题一:为何会出现第二行中的约束条件?
有了这N个约束条件,好像w,b的可选范围小了很多,跟一开始单纯的最大化几何间隔的任意选w,b有所背离啊?等等,这儿需要注意的是,一开始我们目标是最大化几何间隔,这个几何间隔其实是所有样本点的几何间隔中最小值,而所有样本点的几何间隔有可能是正数(被正确划分),也有可能是负数(被错分)。但是我们一开始讨论最大化几何间隔的时候已经默认平面w,b把训练集T中的所有样本点都正确分类了,只有这样我们才会要求“分隔带最胖”啊,如果有错分的,那分隔带越胖就越不好了。因此满足将所有样本点都正确分类的w,b本来就没多少(限制在一定的范围内了,虽然还是有无数种可能),所以原本我们就要求w,b满足![]() ,而且还得要求如下,
,而且还得要求如下,
![]() ,以保证之前
,以保证之前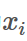 是离超平面w,b最近点的设定。
是离超平面w,b最近点的设定。
重要问题二:能否对约束最优化问题进行简化?因为目前来看被优化的目标函数γ跟w,b和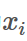 都有关系,有点不简洁。
都有关系,有点不简洁。
解决思路是,对于任意的平面w,b,其实都有无数组参数(λw,λb)λ不为0,都表示该平面。因此我每次选到一个w,b,就相应的知道了最近点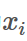 (最近点
(最近点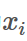 其实是依赖于w,b的,称为支持向量,个人理解也可以称作支持样本点),我都缩放一下w,b,使得函数间隔γ'=1,即:
其实是依赖于w,b的,称为支持向量,个人理解也可以称作支持样本点),我都缩放一下w,b,使得函数间隔γ'=1,即:
![]() 。注意到,缩放w,b前后,其所代表的平面是同一个超平面;而且缩放w,b对于目标函数γ毫无影响,因为其分子分母都是缩放相同的倍数;再者,约束条件的不等号两边都是同时缩放相同的倍数,也无影响。因此,如果我们采用枚举法来求解上述最优化问题(为直观理解,其实是枚举不完的),每次我们随机考察一个平面(w,b),我们都缩放为(w',b')=(λw,λb),使得函数间隔γ'=1,那么我们依旧在考察同一个平面,依旧能算出和缩放前一样的目标函数γ值,依旧符合同样的约束条件。这么处理(特定缩放)有何好处呢?通过这样的处理,我们把约束最优化问题可以转化为如下形式:
。注意到,缩放w,b前后,其所代表的平面是同一个超平面;而且缩放w,b对于目标函数γ毫无影响,因为其分子分母都是缩放相同的倍数;再者,约束条件的不等号两边都是同时缩放相同的倍数,也无影响。因此,如果我们采用枚举法来求解上述最优化问题(为直观理解,其实是枚举不完的),每次我们随机考察一个平面(w,b),我们都缩放为(w',b')=(λw,λb),使得函数间隔γ'=1,那么我们依旧在考察同一个平面,依旧能算出和缩放前一样的目标函数γ值,依旧符合同样的约束条件。这么处理(特定缩放)有何好处呢?通过这样的处理,我们把约束最优化问题可以转化为如下形式:
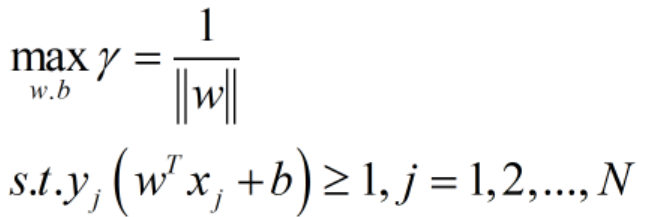
如此形式,简洁明了多了。再者我们可以将max变为min,最大化![]() 与最小化
与最小化![]() 是等价的,就得到了如下线性可分支持向量机学习的最优化问题:
是等价的,就得到了如下线性可分支持向量机学习的最优化问题:

PS:
为加深上述重要问题二的理解,我们可以举一个例子来验证它。
假设有A,B两种w,b的方案,A平面的支持向量(最近点)![]() ,B平面的支持向量
,B平面的支持向量![]() ,我们来比较A,B方案的优劣。
,我们来比较A,B方案的优劣。
1)首先在原始目标函数下,得到两个平面的γ如下:
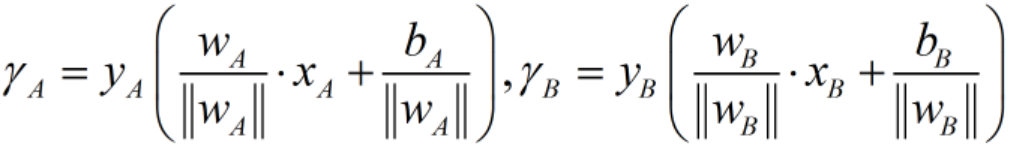
我们假设![]() ,那么我们换种思路来比较A方案与B方案,看看结果是否一致。
,那么我们换种思路来比较A方案与B方案,看看结果是否一致。
2)令![]() ,注意到在给定平面A的情况下这是一个数(其实就是平面A关于训练集T的函数间隔)。
,注意到在给定平面A的情况下这是一个数(其实就是平面A关于训练集T的函数间隔)。
我们令![]() 缩放为
缩放为![]() ,则
,则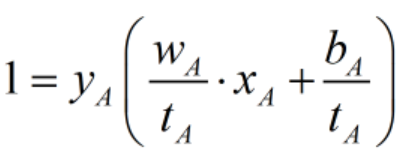 ;
;
同理,对于平面B,我们可以将![]() 缩放为
缩放为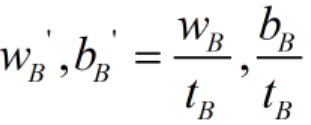 ,则
,则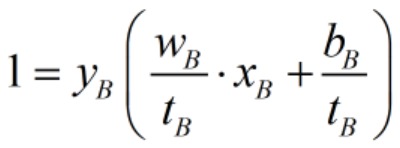 。
。
现在我们通过比较![]() 来确定哪个方案更好,是A还是B?
来确定哪个方案更好,是A还是B?
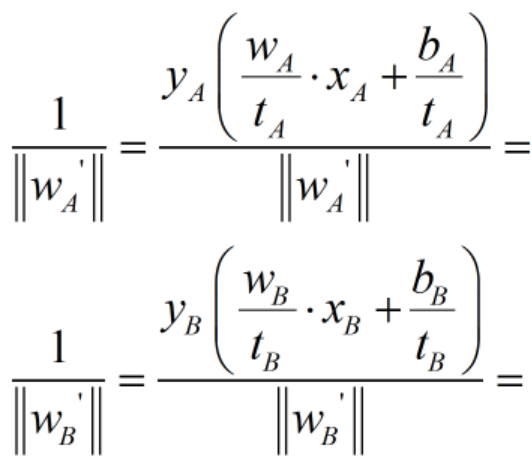
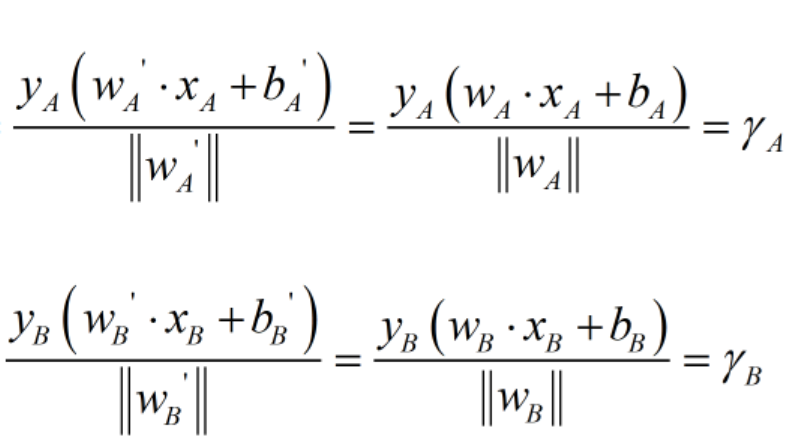
所以我们发现结果是一致的,A优于B,而且目标函数值也与原目标函数值一致。至此,我们验证了准确性,直观感受了w,b缩放前后目标函数值的不变性。