回想一下,当我们在肝无向图连通性时,我们会遇到一个神奇的点——它叫割点。假设现在有一个无向图,它有一个割点,也就是说把割点删了之后图会分成两个联通块A,B。设点u∈A,v∈B,在原图中他们能够互相到达,而删了割点后他们就不能了。于是类似的,我们能不能够在有向图里面也找出这样的“割点”呢?也就是说,现在有两个点u,v,其中u可以到达v;而删去割点后,u不能再到达v。
在解决这个问题前,我们先吃一盘开胃菜——我们先给图中的边都取个名字。众所周知,用深度优先搜索遍历一张图,过程中走过的边和点会共同构成一棵树,它叫做这个图的搜索树。现在我们有一张有向图,我们找出它的搜索树之后,来观察一下这些边:
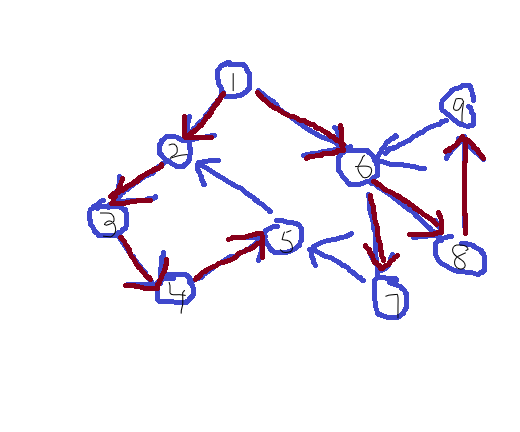
红色边和所连的点就是搜索树。画出这么一个玩意儿之后,我们给这些边都取个名字:
1.树枝边:E(u,v)在搜索树中 2.前向边:搜索树中连向v的边 3.后向边:搜索树中v连出去的边 4.横叉边:不在搜索树上的边
现在我们开始愉快地找规律。我们首先算出这些点的时间戳。假设图中每个点的时间戳都与自己的编号相同(假设是成立的)。先从树枝边开始,我们看E(1->2)并观察两个端点的时间戳,我们会发现,dfn[1]<dfn[2];我们再观察E(2->3),我们又发现dfn[2]<dfn[3];我们再观察E(3->4)......观察完所有的树枝边,我们会发现一个规律:对于任意E(u->v)∈dfs tree,其中u∈V,v∈V,都有dfn[u]<dfn[v]。其实根据时间戳和搜索树的定义也是能够直接推出这个结论的。
由于前向边和后向边都是包含于树枝边的,我们现在先不管它。我们看看横叉边。E(5->2)就是横叉边,我们发现,dfn[5]>dfn[2]。那是不是对于任意E(u->v)∉dfs tree,其中u∈V,v∈V,都有dfn[u]>dfn[v]呢?看完图中所有横叉边之后,我们发现这个猜想仍然成立。但这是不是正确的结论呢?显然是的。下面来证一下,顺便加深一下我们对时间戳和搜索树的认识。
证明:假设我们搜索到了u,且图中存在E(u->v),且v已经被搜索过,现在在搜索树中。设u的时间戳为dfn[v],因为v已经被搜索过,所以E(u->v)不会加入到搜索树中,否则会形成环。易得出dfn[u]>dfn[v],所以对于任意E(u->v)∉dfs tree,其中u∈V,v∈V,都有dfn[u]>dfn[v]。证毕。
好弱鸡的证明。。。但当时证这个的时候确实让我对时间戳和搜索树的认识加深了不少(其实还是我太弱了)。
看完这些乱七八糟的边之后,我们再整些点来玩(sang xin bing kuang)。
先看一下流图的定义:有向图G中,若存在一点r,从r出发能够到达图中所有的点,则称G为流图,记为(G,r)。
于是又有了一些新东西:
1.必经点。若(G,r)中r到v的所有路径都经过点u,则称u是v的必经点,记为u dom v(易懂吧)。v的所有必经点构成的集合记为dom(y),dom(y)={x|x dom y}。
2.最近必经点。最接近v的必经点。首先,v的必经点的dfn肯定<v的dfn,在搜索树上越往上走,dfn越小。所以最接近v的必经点就是dom(v)中dfn最大的那个点。由于最近必经点唯一,可以记为idom(v)。
搞了这么大半天,我们到底要干些什么?!不清楚......啪!好吧,我们来给自己出一题:给定一张有向图(G,r),求出对于每个点,有多少点以它为必经点。
考虑暴力怎么写。考虑特殊情况,我们认为dom(r)={r}。然后对于其余任意点v,考虑它的所有前驱节点的所有必经点。为了方便,我们设v的前驱节点集合为pre。设存在u1∈pre,u2∈pre,并且存在w dom u1。若|pre|=2,即v的前驱节点只有u1,u2,现有两种情况:w dom u2和!(w dom u2)。若是第一种情况,可以推出w同样是v的必经点;而第二种情况则w不是v的必经点。推广为|pre|>=2的情况,我们可以得出v的必经点集合就是v的所有前驱节点的必经点集合的交集,即∩u∈predom(u)。于是我们得出了一种通过前驱节点来更新必经点的做法。所以我们可以从r开始往外算,若是DAG则根据拓补序计算,若是一般图则迭代一下。时间复杂度为O(N2)。但是连模板都跑不了。
那我们换一种思路求解。既然直接求出必经点太过突兀(?),我们为何不通过求出一个弱鸡一点的东西,再进一步求出必经点呢?
所以我们再引入一个概念:
半必经点。能通过走非树枝边到达v的深度最小的v的祖先u。其实这个定义也没说清楚。假设u是v的半必经点,存在一条u到v的路径,把u和v都去掉后,路径上所有点的dfn都大于v的dfn。这样的u就是v的半必经点。当然,若路径上去掉u和v就没点了,那u就是v的半必经点。画个图:
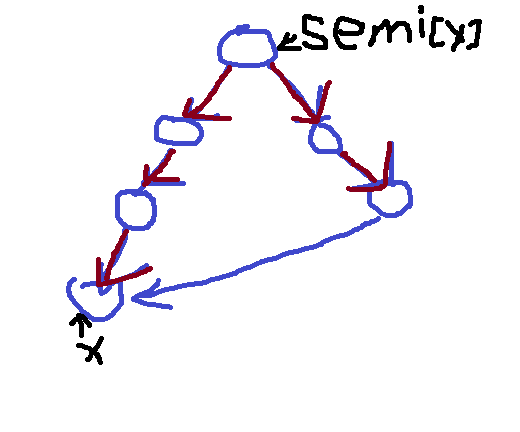
根据那个讲得不是很清楚的定义可以得出,一个点的半必经点是唯一的,u的半必经点记为semi(u)。
可以得出半必经点的一些性质:
1.x的半必经点一定是x在搜索树上的祖先,即dfn[semi[x]]<dfn[x].
2.半必经点不一定是必经点。
3.idom[x]是semi[x]在搜索树上的祖先(semi[x]也是自己的祖先)。
第一条是显而易见的。然后我们看第二条,假设半必经点就是必经点,下面给一个图推翻假设:
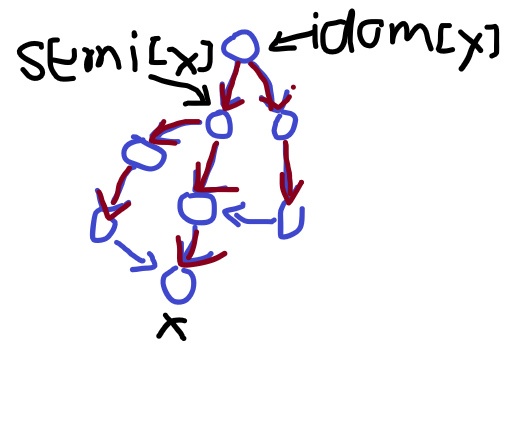
而第三条也是显然成立的,否则idom[x]就会位于semi[x]到x的路径上,而semi[x]到x的路径显然不止一条。
那么我们怎么求半必经点呢?
int tmp=+∞; for(each v∈pre(u)) if(dfn[v]<dfn[u]) tmp=min(tmp,dfn[v]);//E(v,u)为树枝边 else for(each w∈anc(v)) if(dfn[w]>dfn[u]) tmp=min(tmp,dfn[semi[w]]);//E(v,u)为横叉边 semi[u]=id[tmp];
这里的第二层for循环可以省掉。具体的做法是:用带权并查集来维护v的dfn最小的祖先,其权值就是dfn的值,用路径压缩可以达到logN级别,再加上按秩合并可以达到α(N)级别,增长率比log还慢,接近线性。然而我太弱了,只会打路径压缩。。。那么求出所有点的半必经点的时间复杂度就是0(NlogN)。
然而这只是半必经点而已,并不是必经点。所以我们还要通过半必经点来求出必经点。其实是求出最近必经点。
那么最近必经点怎么求呢?设semi[x]到x的路径上去掉了semi[x]之后的点构成的集合为path。
int y=id[min{dfn[semi[z]]|z∈path}]; if(semi[x]==semi[y]) idom[x]=semi[x]; else idom[x]=idom[y];
那么这两个东西的求法怎么证呢?(太弱了证不出来)这一块等层次练高了再补上。
然后就该解决问题了。我们来看一个神奇的东西:支配树。
支配树:从每个点的最近必经点往它连一条有向边。由于每个点的最近必经点是唯一的,所以新连的边和原图的点就构成了一棵树。这棵树叫支配树。也就是说树上的点支配着它的子树嘛。支配树中存在E(u,v)当且仅当u=idom(v)。树中存在u到v的路径当且仅当u dom v。
所以我们可以先求出有向图的支配树,那么对于一个点,它是多少点的必经点就等于它在支配树中有多少儿子了。怎么求呢?求支配树有一个算法,由Lengauer和Tarjan提出,那名字当然叫Lengauer-Tarjan啦~这个算法的原理是:
1.建出搜索树并算出每个点的时间戳
2.根据半必经点定理按时间戳从大到小计算出每个点的半必经点
3.根据必经点定理,通过算出的半必经点得出每个点的最近必经点
具体的过程:
1.每计算一个点时,把这个点放进生成森林中,用并查集维护
2.根据半必经点定理,若dfn[x]>dfn[y],计算semi[y]时则需要考虑x祖先中dfn大于y的点
3.由于按时间戳从大到小的顺序计算,比y时间戳小的点还未加入生成森林,所以直接在生成森林中考虑x的祖先即可
4.令dfn[semi[x]]为x到其父亲的边的权值,用带权并查集可以求出边权的最小值
于是代码就能写得出来:
#include <stdio.h> #include <string.h> #define maxn 200001 #define maxm 300001 struct graph{ struct edge{ int to,next; edge(){} edge(const int &_to,const int &_next){ to=_to,next=_next; } }e[maxm]; int head[maxn],k; inline void init(){ memset(head,-1,sizeof head); } inline void add(const int &u,const int &v){ e[k]=edge(v,head[u]),head[u]=k++; } }a,b,c,d; inline int read(){ register int x(0); register char c(getchar()); while(c<'0'||'9'<c) c=getchar(); while('0'<=c&&c<='9') x=(x<<1)+(x<<3)+(c^48),c=getchar(); return x; } int bel[maxn],val[maxn],semi[maxn],idom[maxn]; int fa[maxn],dfn[maxn],id[maxn],tot; int n,m,size[maxn]; void dfs(int u){ dfn[u]=++tot,id[tot]=u; for(register int i=a.head[u];~i;i=a.e[i].next){ int v=a.e[i].to; if(!dfn[v]){ fa[v]=u; dfs(v); } } } int find(int u){ if(bel[u]==u) return u; int tmp=find(bel[u]); if(dfn[semi[val[bel[u]]]]<dfn[semi[val[u]]]) val[u]=val[bel[u]]; return bel[u]=tmp; } inline void lengauer_tarjan(){ int u,v; for(register int i=tot;i>1;i--){ u=id[i]; for(register int i=b.head[u];~i;i=b.e[i].next){ if(dfn[v=b.e[i].to]){ find(v);//带权并查集维护最小边权 if(dfn[semi[val[v]]]<dfn[semi[u]]) semi[u]=semi[val[v]]; } } c.add(semi[u],u); bel[u]=fa[u],u=fa[u]; for(register int i=c.head[u];~i;i=c.e[i].next){ find(v=c.e[i].to); if(semi[val[v]]==u) idom[v]=u; else idom[v]=val[v]; }//半必经点定理 } for(register int i=2;i<=tot;i++){ u=id[i]; if(idom[u]!=semi[u]) idom[u]=idom[idom[u]]; }//必经点定理 } void dfs_ans(int u){ size[u]=1; for(register int i=d.head[u];~i;i=d.e[i].next){ int v=d.e[i].to; dfs_ans(v); size[u]+=size[v]; } } int main(){ a.init(),b.init(),c.init(),d.init(); n=read(),m=read(); for(register int i=1;i<=m;i++){ int u=read(),v=read(); a.add(u,v),b.add(v,u); } dfs(1); for(register int i=1;i<=n;i++) bel[i]=val[i]=semi[i]=i; lengauer_tarjan(); for(int i=2;i<=n;i++) d.add(idom[i],i); dfs_ans(1); for(register int i=1;i<=n;i++) printf("%d ",size[i]);puts(""); return 0; }
等厉害一点了再回来写证明......(逃)