一般的二叉堆支持的操作有插入任意值并调整堆,删除最小值并调整堆,调整堆之后我们可以O(1)取得最小的结点,这是相对于小根堆而言的
这里补充说明一下优先队列不能完成但是二叉堆可以完成的事情,那就是删除指定位置元素的值,优先队列只允许弹出堆顶元素
但是一般的二叉堆可以删除任意元素
1 inline void remove(int p) 2 { 3 q[p]=q[n--]; 4 up(p),down(p); 5 }
这是对之前介绍的手写堆的一个补充
对于STL堆而言,调整元素位置之后重新建堆就好了
然后如果要合并两个堆,如果是普通的二叉堆的话,只能够暴力重构
时间复杂度O(n),可并堆是这样的一类堆,它们在将两个堆合并的时候至多是O(logn)的时间复杂度
然后我们接触其中的一种,性价比最高的一种,左偏树
性质不再描述,这里贴一张图,意会即可
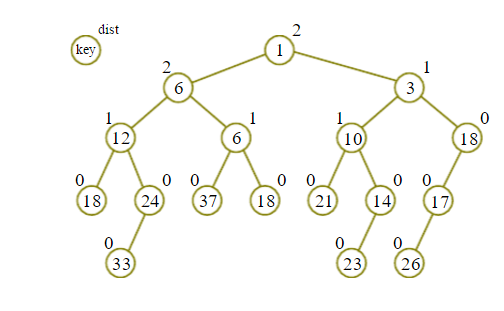
然后看一道BZOJ1367

怎么想出来的我是不会的,但是能够看懂这个解法已经很可以了
首先考虑一个情况,如果t序列本身是一个递增的,那么z序列和它一模一样答案就很显然了
如果t序列是一个递减的,那么当我们知道了这个序列的中位数之后,用t序列中的每一个数减去这个中位数,所得的结果一定是最小的
可以这样考虑问题,我们把t序列分段,对于每一段维护其区间中位数
每当新加进来一个数,就形成单独的一个段
然后比较这两段的中位数,如果前一段的中位数比后一段的中位数要小,满足题意
如果前一段的中位数大于后一段的中位数的话,就要把这两个段合并
然后介绍一下如何使用堆来维护区间中位数
维护一个大根堆,堆里的元素个数等于区间长度的一半,里面保存的数是区间中较小的一半数。那么很显然中位数就是堆顶元素
在问题的最后有一个细节处理
这样求出来的z[i]是单调不减,并不保证单调递增
开始的时候将每一个t[i]减去i,然后按照该方法计算z[i],这样就相当于所有z[i]都加上了i,就把不减转化成了递增
1 #include<cmath> 2 #include<cstdio> 3 #include<algorithm> 4 using namespace std; 5 const int maxn=1000005; 6 int n,now; 7 int a[maxn],root[maxn],L[maxn],R[maxn],tot[maxn]; 8 long long ans; 9 inline int read() 10 { 11 int x=0,f=1;char ch=getchar(); 12 while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} 13 while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} 14 return x*f; 15 } 16 struct Ltree 17 { 18 int cnt; 19 int l[maxn],r[maxn]; 20 int v[maxn],siz[maxn],d[maxn]; 21 int merge(int x,int y) 22 { 23 if(x==0||y==0) return x+y; 24 if(v[x]<v[y]) swap(x,y); 25 r[x]=merge(r[x],y); 26 siz[x]=siz[l[x]]+siz[r[x]]+1; 27 if(d[r[x]]>d[l[x]]) swap(l[x],r[x]); 28 d[x]=d[r[x]]+1; 29 return x; 30 } 31 int top(int x) 32 { 33 return v[x]; 34 } 35 int size(int x) 36 { 37 return siz[x]; 38 } 39 void pop(int &x) 40 { 41 x=merge(l[x],r[x]); 42 } 43 int new_heap(int x) 44 { 45 v[++cnt]=x; 46 siz[cnt]=1; 47 l[cnt]=r[cnt]=d[cnt]=0; 48 return cnt; 49 } 50 }heap; 51 int main() 52 { 53 n=read(); 54 for(int i=1;i<=n;i++) a[i]=read()-i; 55 for(int i=1;i<=n;i++) 56 { 57 now++; 58 root[now]=heap.new_heap(a[i]); 59 tot[now]=1; 60 L[now]=R[now]=i; 61 while(now>1&&heap.top(root[now-1])>heap.top(root[now])) 62 { 63 now--; 64 root[now]=heap.merge(root[now],root[now+1]); 65 tot[now]+=tot[now+1];R[now]=R[now+1]; 66 while(heap.size(root[now])*2>tot[now]+1) 67 heap.pop(root[now]); 68 } 69 } 70 for(int i=1;i<=now;i++) 71 for(int j=L[i],t=heap.top(root[i]);j<=R[i];j++) 72 ans+=abs(a[j]-t); 73 printf("%lld",ans); 74 return 0; 75 }