一、基本概念
在介绍最长公共公共子序列之前,先说一下这里的基本概念。
1.串和序列:
串: 串是一个连续的部分。比如在12345这个数列中,123这个是一个串,45也是一个串。而135不是一个串。
序列:子序列则是从不改变序列的顺序,而从序列中去掉任意的元素而获得新的序列。还是12345这个数列,135是一个序列,24也是一个序列,当然123也是一个序列。
异同:串中字符的位置必须是连续的,序列则可以不必连续。
2.子串和子序列
就是一个数列或者字符列的一部分。子串就是位置连续的一部分,子序列就是不必连续的一部分。
3.最长上升子序列(LIS)
就是在子序列的基础上添加了两个定语。上升就是按一个顺序(升序、降序、非上升、非下降等),最长就是最长的一部分。
最长上升子序列就是指一个序列中最长的单调递增的子序列
比如在1352496这个序列中,546(随便举得例子)是一个子序列,但不是上升子序列。3 5 6(也是随便举得例子)就是一个上升子序列。
但是不是最长的,1 3 4 9则是一个最长的上升子序列。同样1 2 4 6也是一个最长的上升子序列。所以最长上升子序列并不一定是唯一的。
4.最长公共子序列(LCS)
有了公共这个定语,那么至少就是在两个数列或者字符列中找最长的公共的部分。就是说一个数列 ,如果分别是两个或多个已知数列的子序列,且是所有符合此条件序列中最长的,则称为是最长公共子序列。
比如在1352496和382546这两个序列中,3 4是公共子序列,2 4 也是公共子序列。但不是最长的,最长的公共子序列为3 2 4 6。
二、最长上升子序列
①算法1(n^2)
我们依次遍历整个序列,每一次求出从第一个数到当前这个数的最长上升子序列,直至遍历到最后一个数字为止
然后再取dp数组里最大的那个即为整个序列的最长上升子序列。
我们用dp[i]来存放序列1-i的最长上升子序列的长度,那么dp[i]=max(dp[j])+1,(j∈[1, i-1]);
显然dp[1]=1,我们从i=2开始遍历后面的元素即可。
模板:
#include<stdio.h> int main() { int n,i,j,num,h[1000],max[1000]; while(~scanf("%d",&n)) { num=1; for(i=0; i<n; ++i) { scanf("%d",&h[i]); max[i]=1; } for(i=1; i<n; ++i)/*求最长上升子序列*/ for(j=0; j<i; ++j) { if(h[j]<h[i]&&max[j]+1>max[i])/*用两个数组,方便理解,如果只是求最长上升子序列,可以直接max[j]和num比较取较大值*/ max[i]=max[j]+1; if(num<max[i]) num=max[i]; } printf("%d ",num); } return 0; }
②算法2(nlogn):
维护一个一维数组c,并且这个数组是动态扩展的,初始大小为1,
c[i]表示最长上升子序列长度是i的所有子串中末尾最小的那个数,根据这个数字,我们可以比较知道,
只要当前考察的这个数比c[i]大,那么当前这个数一定能通过c[i]构成一个长度为i+1的上升子序列。
当然我们希望在C数组中找一个尽量靠后的数字,这样我们得到的上升子串的长度最长,查找的时候使用二分搜索,这样时间复杂度便下降了。
举例说明一下(复制自某大牛):
假设存在一个序列d[1..9] = 2 1 5 3 6 4 8 9 7,可以看出来它的LIS长度为5。
下面一步一步试着找出它。
我们定义一个序列B,然后令 i = 1 to 9 逐个考察这个序列。
此外,我们用一个变量Len来记录现在最长算到多少了
首先,把d[1]有序地放到B里,令B[1] = 2,就是说当只有1一个数字2的时候,长度为1的LIS的最小末尾是2。这时Len=1
然后,把d[2]有序地放到B里,令B[1] = 1,就是说长度为1的LIS的最小末尾是1,d[1]=2已经没用了,很容易理解吧。这时Len=1
接着,d[3] = 5,d[3]>B[1],所以令B[1+1]=B[2]=d[3]=5,就是说长度为2的LIS的最小末尾是5,很容易理解吧。这时候B[1..2] = 1, 5,Len=2
再来,d[4] = 3,它正好加在1,5之间,放在1的位置显然不合适,因为1小于3,长度为1的LIS最小末尾应该是1,这样很容易推知,长度为2的LIS最小末尾是3,于是可以把5淘汰掉,这时候B[1..2] = 1, 3,Len = 2
继续,d[5] = 6,它在3后面,因为B[2] = 3, 而6在3后面,于是很容易可以推知B[3] = 6, 这时B[1..3] = 1, 3, 6,还是很容易理解吧? Len = 3 了噢。
第6个, d[6] = 4,你看它在3和6之间,于是我们就可以把6替换掉,得到B[3] = 4。B[1..3] = 1, 3, 4, Len继续等于3
第7个, d[7] = 8,它很大,比4大,嗯。于是B[4] = 8。Len变成4了
第8个, d[8] = 9,得到B[5] = 9,嗯。Len继续增大,到5了。
最后一个, d[9] = 7,它在B[3] = 4和B[4] = 8之间,所以我们知道,最新的B[4] =7,B[1..5] = 1, 3, 4, 7, 9,Len = 5。
于是我们知道了LIS的长度为5。
注意。这个1,3,4,7,9不是LIS,它只是存储的对应长度LIS的最小末尾。有了这个末尾,我们就可以一个一个地插入数据。虽然最后一个d[9] = 7更新进去对于这组数据没有什么意义,但是如果后面再出现两个数字 8 和 9,那么就可以把8更新到d[5], 9更新到d[6],得出LIS的长度为6。
模板:
#include <cstdio> #include <cstring> #include <algorithm> #include <iostream> #define MAXN 40005 using namespace std; int arr[MAXN],ans[MAXN],len; int main() { int n; int T; cin>>T; while(T--) { cin>>n; for(int i=1; i<=n; ++i) scanf("%d",&arr[i]); ans[1] = arr[1]; len=1; for(int i=2; i<=n; ++i) { if(arr[i]>ans[len]) ans[++len]=arr[i]; else { int pos=lower_bound(ans,ans+len,arr[i])-ans; ans[pos] = arr[i]; } } cout<<len<<endl; } return 0; }
顺便附上手写的二分
int binary_search(int i) { int left,right,mid; left=0,right=len; while(left<right) { mid = left+(right-left)/2; if(ans[mid]>=arr[i]) right=mid; else left=mid+1; } return left; } //int pos=binary_search(i) 这样调用就好了
三、最长公共子序列
引进一个二维数组c[][],用c[i][j]记录X[i]与Y[j] 的LCS 的长度,b[i][j]记录c[i][j]是通过哪一个子问题的值求得的,以决定搜索的方向。
我们是自底向上进行递推计算,那么在计算c[i,j]之前,c[i-1][j-1],c[i-1][j]与c[i][j-1]均已计算出来。此时我们根据X[i] = Y[j]还是X[i] != Y[j],就可以计算出c[i][j]。
状态转移方程如下:
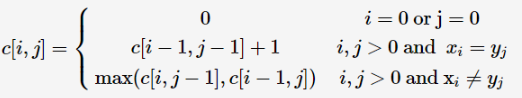
首先做初始化。将c[0][i]和从c[i][0]初始化为0,然后一行一行的填表。
代码:
#include<cstring> #include<cmath> #include<cstring> #include<cstdio> const int qq=1e3+10; char x[qq],y[qq]; int dp[qq][qq]; int main() { while(~scanf("%s%s",x+1,y+1)) { x[0]=y[0]='.'; int len=strlen(x)>strlen(y)?strlen(x):strlen(y); for(int i=0; i<=len; ++i) dp[i][0]=dp[0][i]=0; for(int j,i=1; i<strlen(x); ++i) for(j=1; j<strlen(y); ++j) if(x[i]==y[j]) dp[i][j]=dp[i-1][j-1]+1; else dp[i][j]=dp[i-1][j]>dp[i][j-1]?dp[i-1][j]:dp[i][j-1]; printf("%d ",dp[strlen(x)-1][strlen(y)-1]); } return 0; }
三、最长公共子串
明白了最长公共子序列后,最长上升字串特别简单,状态转移方程如下:
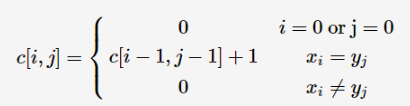
代码如下:
#include<cstring> #include<cmath> #include<cstring> #include<cstdio> const int qq=1e3+10; char x[qq],y[qq]; int dp[qq][qq]; int main() { while(~scanf("%s%s",x+1,y+1)) { int max_len=0; for(int i=0; i<strlen(x); i++) { for(int j=0; j<strlen(y); j++) { if(x[i]==y[j]) { if(i>0&&j>0) { dp[i][j]=dp[i-1][j-1]+1; } else { dp[i][j]=1; } if(max_len<dp[i][j]) { max_len=dp[i][j]; } } } } printf("%d ",max_len); } return 0; }