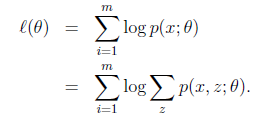最大期望算法(Expectation-Maximization algorithm, EM),或Dempster-Laird-Rubin算法,是一类通过迭代进行极大似然估计(Maximum Likelihood Estimation, MLE)的优化算法,通常作为牛顿迭代法(Newton-Raphson method)的替代用于对包含隐变量(latent variable)或缺失数据(incomplete-data)的概率模型进行参数估计。
EM算法推导
给定的训练样本是![]() ,m个独立样本,我们想找到每个样例隐含的类别z,能使得p(x,z)最大。p(x,z)的最大似然估计如下:
,m个独立样本,我们想找到每个样例隐含的类别z,能使得p(x,z)最大。p(x,z)的最大似然估计如下:
《统计学习方法》第9章 EM算法及其推广
EM算法是一种迭代算法,用于含有隐含变量(hidden variable)的概率模型参数的极大似然估计,或极大后验概率估计。
EM算法的每次迭代由两步组成:
- E步,求期望(expectation);
- M步,求极大(maximization)。
所以这一算法成为期望极大算法(expectation maximization algorithm),简称EM算法。
1. EM算法的引入
概率模型有时既含有观测变量(observable variable),又含有隐变量或潜在变量(latent variable)。如果概率模型的变量都是观测变量,那么给定数据,可以直接用极大似然估计法,或贝叶斯估计发估计模型参数。但是,当模型含有隐变量时,就不能简单地使用这些估计方法。EM算法就是含有隐变量的概率模型参数的极大似然估计法,或极大后验概率估计法。我们在这里只讨论极大似然估计,极大后验概率估计与其类似。
1.1 EM算法
首先介绍一个使用EM算法的例子。
三硬币模型 假设有3枚硬币,分别记作A,B,C。这些硬币正面出现的概率分别是$ pi $、$ p $、$ q $。进行如下抛硬币试验:先掷硬币A,根据其结果选出硬币B或硬币C,正面选硬币B,反面选硬币C;然后掷选出的硬币,掷硬币的结果,出现正面记作1,出现反面记作0;独立地重复n次试验(这里,n=10),观测结果如下:
1, 1, 0, 1, 0, 0, 1, 0, 1, 1
假设只能观测到掷硬币的结果,不能观测掷硬币的过程。问如何估计三硬币正面出现的概率,即三硬币模型的参数。
解 三硬币模型可以写作
$ P(y| heta)=sum_{z}{P(y,z| heta)}=sum_{z}{P(z| heta)P(y|z, heta)}=pi p^y(1-p)^{1-y}+(1-pi)q^y(1-q)^{1-y} $
这里,随机变量y是观测变量,表示一次试验观测的结果是1或0;随机变量z是隐变量,表示未观测到的掷硬币A的结果;$ heta=(pi,p,q) $是模型参数。这一模型是以上数据的生成模型。
将观测数据表示为$ Y=(Y_1,Y_2,…,Y_n)^T $,未观测数据表示为$ Z=(Z_1,Z_2,…,Z_n)^T $,则观测数据的似然函数为:
$ P(Y| heta)=sum_{Z}{P(Z| heta)P(Y|Z, heta)} $
即
$ P(Y| heta)=prod_{j=1}^{n}{[pi p^{y_j}(1-p)^{1-y_j}+(1-pi)q^{y_j}(1-q)^{1-y_j}]} $
考虑求模型参数$ heta=(pi,p,q) $的极大似然估计,即
$ hat{ heta}=argmax_{ heta}{log P(Y| heta)} $
这个问题只能通过迭代的方法求解。
EM算法首先选取参数的初值,记作$ heta^{(0)}=(pi^{(0)},p^{(0)},q^{(0)}) $,然后通过下面的步骤迭代计算参数的估计值,直至收敛为止。
第i次迭代参数的估计值为$ heta^{(i)}=(pi^{(i)},p^{(0)},q^{(i)}) $,EM算法的第i+1次迭代如下:
E步:计算在模型参数$ pi^{(i)} $,$ p^{(i)} $,$ q^{(i)} $下观测数据$ y_j $来自掷硬币B的概率
$ mu^{(i+1)}= frac{pi^{i}(p^{(i)})^{y_j}(1-p^{(i)})^{1-y_j}}{pi^{i}(p^{(i)})^{y_j}(1-p^{(i)})^{1-y_j}+(1-pi^{i})(q^{(i)})^{y_j}(1-q^{(i)})^{1-y_j}} $
M步:计算模型参数的新估计值
$ pi^{(i+1)}=frac{1}{n}sum_{j=1}^{n}{mu_j^{(i+1)}} $
$ p^{(i+1)}=frac{sum_{j=1}^{n}{mu_j^{(i+1)}y_j}}{sum_{j=1}^{n}{mu_j^{(i+1)}}} $
$ q^{(i+1)}=frac{sum_{j=1}^{n}{(1-mu_j^{(i+1)})y_j}}{sum_{j=1}^{n}{(1-mu_j^{(i+1)})}} $
假设模型参数的初值取为
$ pi^{(0)}=0.5 $, $ p^{(0)}=0.5 $, $ q^{(0)}=0.5 $
利用迭代公式,得到模型参数$ heta$的极大似然估计:
$ hat{pi}=0.5 $ , $ hat{p}=0.6 $, $ hat{q}=0.6 $
一般地,用Y表示观测随机变量的数据,Z表示隐随机变量的数据。Y和Z连在一起称为完全数据(complete-data),观测数据Y又称为不完全数据(incomplete-data)。假设给定观测数据Y,其概率分布是$ P(Y| heta) $,其中$ heta $是需要估计的模型参数,那么不完全数据Y的似然函数是$ P(Y| heta) $,对数似然函数$ L( heta)=log P(Y| heta) $;假设Y和Z的联合概率分布是$ P(Y,Z| heta) $,那么完全数据的对数似然函数是$ log P(Y,Z| heta) $。
EM算法通过迭代求$ L( heta)=log P(Y| heta) $的极大似然估计。每次迭代包括两步:E步,求期望;M步,求极大化。下面来介绍EM算法。