折线分割平面
Time Limit: 2000/1000ms (Java/Others)
Problem Description:
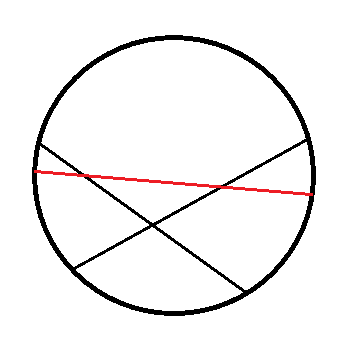
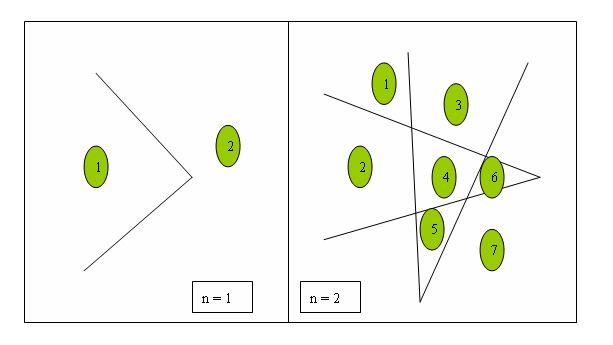
我们看到过很多直线分割平面的题目,今天的这个题目稍微有些变化,我们要求的是n条折线分割平面的最大数目。比如,一条折线可以将平面分成两部分,两条折线最多可以将平面分成7部分,具体如下所示:
Input:
输入数据的第一行是一个整数C,表示测试实例的个数,然后是C 行数据,每行包含一个整数n(0<n<=10000),表示折线的数量。
Output:
对于每个测试实例,请输出平面的最大分割数,每个实例的输出占一行。
Sample Input:
3 1 2 12
Sample Output:
2 7 277
解题思路:首先来看看直线分割平面的情况:在一个平面上有一个圆和n条直线,这些直线中每一条在圆内同其他直线相交,假设没有3条直线相交于一点,试问这些直线将圆分成多少个区域。
分析:当添加第n条直线时,为了使圆分割成更多的区域,第n条直线要与前n-1条直线都相交,且没有任何三条直线相较于一点,则添加第n条直线会多出n-1个交点。由于每增加n个交点,就会增加n+1个区域(比如原来圆中有2条直线、1个交点、4个区域,现多加了1条红色的直线,则多加了2个交点,共有3个交点,区域个数也多加了3个,一共把圆分成7个区域),所以添加第n条直线会在原来的基础上增加n个区域。假设f(n)表示n条直线把圆内分成区域的个数,则易得递推式:f(n)=f(n-1)+n。
现在再来考虑折线分割平面的情况:平面上有n条折线,问这些折线最多能将平面分割成多少区域。
分析:由直线分割平面的结论可知,平面内原来直线与直线的交点个数决定了新增直线交点的个数,进而决定新增区域的个数。同理,当添加第n条折线时,为了使圆内分割成更多的区域,第n条折线的2条射线要与前n-1条折线相交,且没有三条射线相交于一点,则添加第n条折线会多出2*2(n-1)=4(n-1)个交点。由于每增加1个交点,就会增加2个区域,所以添加第n条折线会在原来的基础上增加4*(n-1)+1个区域。假设f(n)表示n条折线把圆内分成区域的个数,则易得递推式:f(n)=f(n-1)+4*(n-1)+1=f(n-1)+4*n-3。
1 #include<bits/stdc++.h> 2 using namespace std; 3 int main() 4 { 5 int c,n,sum[10005]={1,2};//没有折线时只有一个平面块 6 for(int i=2;i<10005;++i) 7 sum[i]=sum[i-1]+4*i-3; 8 while(cin>>c){ 9 while(c--){ 10 cin>>n; 11 cout<<sum[n]<<endl; 12 } 13 } 14 return 0; 15 }
再来看看两道变形题:
M线分割平面(小数据)
Time Limit: 2000/1000ms (Java/Others)
Problem Description:
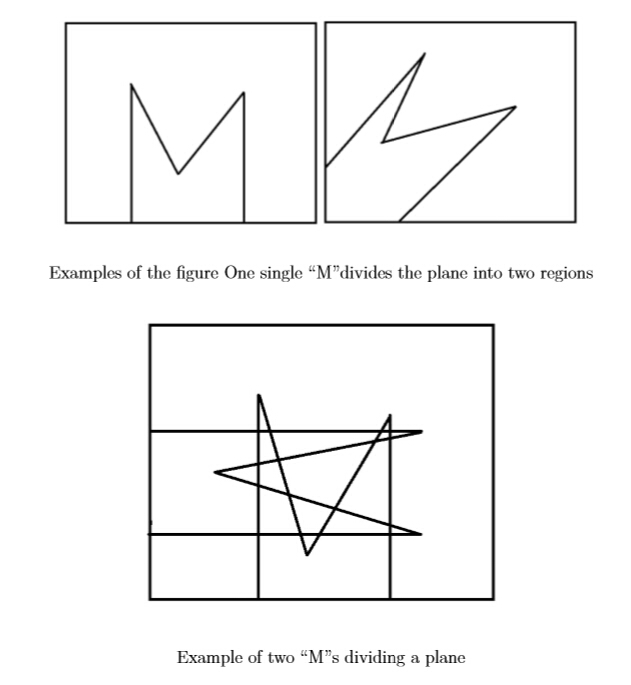
分割平面的题大家不会陌生了。 1条直线最多能把平面分割为2部分; 2条直线最多能把平面分割为4部分; 3条直线最多能把平面分割为7部分; 。。。等等。。。 这是用直线分割平面的, 现在我们用M来分割平面。 如图所示例子。
Input:
输入首先输入一个整数T(1 ≤ T ≤ 1000),接下来有T组数据,每组数据输入一个数N (0 ≤ N ≤ 10000),代表着M的个数。
Output:
对于每组数据,输出N个M最大能分割的平面数,格式参照样例输出。
Sample Input:
2 1 2
Sample Output:
Case #1: 2 Case #2: 19
解题思路:由上面的规律易得递推式:f(n)=f(n-1)+4*4(n-1)+1=f(n-1)+16*n-15。
AC代码:
1 #include<bits/stdc++.h> 2 using namespace std; 3 int main(){ 4 int t,n,sum[10001]={1,2}; 5 for(int i=2;i<10001;++i) 6 sum[i]=sum[i-1]+16*i-15; 7 while(cin>>t){ 8 for(int i=1;i<=t;++i){ 9 cin>>n; 10 cout<<"Case #"<<i<<": "<<sum[n]<<endl; 11 } 12 } 13 return 0; 14 }
N线分割平面
Time Limit: 2000/1000ms (Java/Others)
Problem Description:
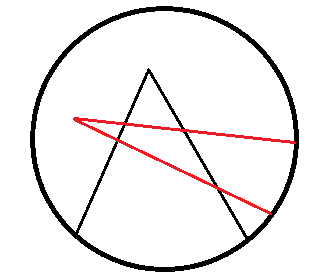
N型折线分割,如图,一个N型折线可以最多把平面分成2份,两个可以最多分成12份。那么n个N型折线可以最多把平面分成几份?
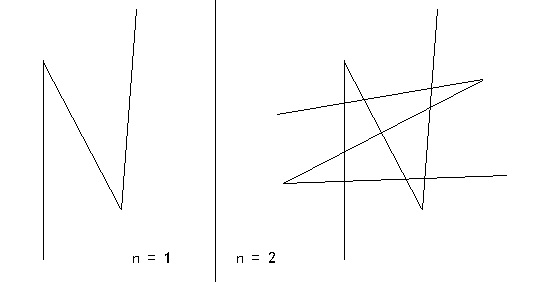
Input:
输入数据的第一行是一个整数C,表示测试实例的个数,然后是C 行数据,每行包含一个整数n(0<n<=10000),表示N型折线的数量。
Output:
对于每个测试实例,请输出平面的最大分割数,每个实例的输出占一行。
Sample Input:
2 1 2
Sample Output:
2 12
解题思路:由上面的规律易得递推式:f(n)=f(n-1)+3*3(n-1)+1=f(n-1)+9*n-8。
AC代码:
1 #include<bits/stdc++.h> 2 using namespace std; 3 int main(){ 4 int c,n,sum[10001]={1,2}; 5 for(int i=2;i<10001;++i) 6 sum[i]=sum[i-1]+9*i-8; 7 while(cin>>c){ 8 while(c--){cin>>n;cout<<sum[n]<<endl;} 9 } 10 return 0; 11 }
以上规律只适用于不是封闭曲线(特定直线构成的图形)的所有情况。
接下来看看封闭曲线分割平面的情况:设有n条封闭曲线画在平面上,而任何两条封闭曲线恰好相交于两点,且任何三条封闭曲线不相交于同一点,问这些封闭曲线把平面分割成区域的个数。
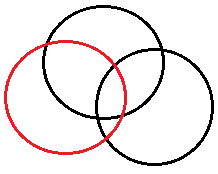
分析:先找找规律:当n=1时,封闭曲线上有0个交点,平面被分成了2个区域;当n=2时,为了使平面分成更多的区域,则第二条封闭曲线必须和前面1条曲线中每条曲线都有2个新的交点,一共就多出了2*1个新的交点,此时对应增加了2*1个区域,平面被分成了2+2=4个区域;当n=3时,同理且任何三条封闭曲线不相交于同一点,则第三条封闭曲线必须和前面2条曲线中每条曲线都有2个新的交点,一共就多出了2*2=4个新的交点,此时对应增加了4个区域,平面被分成了4+4=8个区域......由此可以推出当添加第n条封闭曲线时,其必须与前面n-1条曲线中每条曲线都有2个新的交点,一共就多出了2*(n-1) 个新的交点,此时对应增加了2*(n-1)个区域,所以添加第n条封闭曲线就会在原来的基础上多出2*(n-1)个区域。假设f(n)表示n条封闭曲线把平面分成区域的个数,则易得递推式:f(n)=f(n-1)+2*(n-1)。
实战:题解报告:hdu 1249 三角形
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=1249
Problem Description
Input
Output
Sample Input
Sample Output

1 #include<bits/stdc++.h> 2 using namespace std; 3 int main(){ 4 int c,n,sum[10001]={1,2}; 5 for(int i=2;i<10001;++i) 6 sum[i]=sum[i-1]+6*(i-1); 7 while(cin>>c){ 8 while(c--){ 9 cin>>n; 10 cout<<sum[n]<<endl; 11 } 12 } 13 return 0; 14 }
最后讲讲平面分割空间的情况:由二维平面分割问题可以得出规律,交点的个数决定新增区域的个数,换一下思路,我们同样能在三维中找到递推式。当n=1时,空间中有0条交线,整个空间被分成2个区域;当n=2时,为了使空间分成更多的区域,则第2个平面必须与前面1个平面中每1个平面都有1条新的交线,此时第2个平面被分成2个区域,相应增加了2个空间区域,整个空间一共被分成2+2=4个区域;当n=3时,由于任何3个平面都不会相交于同一条直线,第3个平面必须与前面2个平面中每一个平面都有一条新的交线,并且此时第3个平面有2条相交直线将其分成4个区域,相应增加了4个空间区域,整个空间一共被分成4+4=8个区域......由此可以推出当添加第n个平面时,其必需与前面n-1个平面都有一条新的交线,且第n个平面有n-1条直线分割该平面,假设sum(n)表示n个平面将空间分成区域的个数,f(n)表示n条直线将平面分成区域的个数,则易得递推式sum(n)=sum(n-1)+f(n-1),(其中f(n)=f(n-1)+n)。
实战:题解报告:hdu 1290 献给杭电五十周年校庆的礼物
Problem Description
或许你依然心怀忧伤
或许你近在咫尺
或许你我天各一方
对于每一个学子
母校
永远航行在
生命的海洋
今年是我们杭电建校五十周年,这是一个值得祝福的日子。我们该送给母校一个怎样的礼物呢?对于目前的大家来说,最好的礼物当然是省赛中的好成绩,我不能参赛,就送给学校一个DOOM III球形大蛋糕吧,这可是名牌,估计要花掉我半年的银子呢。
想象着正式校庆那一天,校长亲自操刀,把这个大蛋糕分给各地赶来祝贺的校友们,大家一定很高兴,呵呵,流口水了吧...
等一等,吃蛋糕之前先考大家一个问题:如果校长大人在蛋糕上切了N刀(校长刀法极好,每一刀都是一个绝对的平面),最多可以把这个球形蛋糕切成几块呢?
做不出这个题目,没有蛋糕吃的!
为-了-母-校-,为-了-蛋-糕-(不是为了DGMM,枫之羽最会浮想联翩...),加-油-!
Input
Output
Sample Input
Sample Output
1 #include<bits/stdc++.h> 2 using namespace std; 3 int main(){ 4 int n,sum[1001]={1,2},f[1001]={1,2}; 5 for(int i=2;i<1001;++i) 6 sum[i]=sum[i-1]+(f[i-1]=f[i-2]+i-1); 7 while(cin>>n){cout<<sum[n]<<endl;} 8 return 0; 9 }