不错的一道题。
题意:每次修改一栋楼,求这些楼顶跟原点$(0,0)$的斜率单调上升长度(不是$ ext{LIS}$)。
因为一个楼房能被看到可以等价于它的斜率比之前的任何一个都大。
这道题实际上满足区间合并,但是比较麻烦。
重点就在$ ext{pushup}$的写法。
首先定义线段树中区间的解即为该对应区间内的单调上升长度。
两个区间的合并:
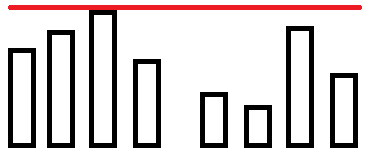
如图,发现右区间会受左区间的影响。
左区间的答案为$3$,右区间的答案为$2$,但在合并后为$3$。
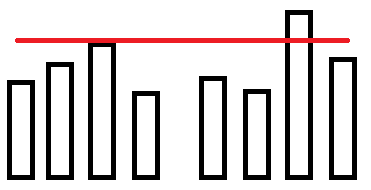
而这样的话合并后为$4$。
所以右区间的答案主要受左区间最大值的影响。
令$cnt[o]$为结点$o$的答案,所以维护中一定有$cnt[o]=cnt[lson]+get\_ans(cnt[rson])$。
如何$get\_ans$呢?
发现右区间受左区间最大值影响,所以一定受到$maxv[lson]$的约束。
观察如下

如果$B$受到$A$的约束,那么$C$、$D$也会受到$A$的约束。然后$D$也会受到$C$的约束。
如果$D$受到的约束中$A$没有$C$强,即$maxv[A]<maxv[C]$,那么只需递归处理$C$的区间再加上$D$贡献的答案(这里有个小细节,放后面谈)。
因为区间$A,C$中最高的仍为$maxv[C]$。
反之只需递归处理$D$区间,答案无需加上$C$(因为都被$A$挡住了)。
当递归到边界了,也就只剩一个数了$maxv$,只要判断是否大于约束即可(解为$0//1$)
递归过程中不需要修改$cnt$,因为区间内无需考虑区间外的影响(要想明白)。
根据以上可以得到下面的$ ext{pushup}$:
1 int pushup(int o, int l, int r, double d) { 2 if (l == r) return maxv[o]-d > 1e-10 ? 1: 0; 3 int mid = (l + r) >> 1; 4 if (maxv[lson]-d > 1e-10) { // l > d 5 return pushup(lson, l, mid, d) + cnt[o] - cnt[lson]; 6 } else { // l <= d 7 return pushup(rson, mid+1, r, d); 8 } 9 }
$d$表示约束,递归时需要下传。
上面谈到了一个问题:加上$D$贡献的答案。
这里是
return pushup(lson, l, mid, d) + cnt[o] - cnt[lson];
而不是
return pushup(lson, l, mid, d) + cnt[rson];
要理解两者的差别:
后者是右区间不受左区间约束下的解;而前者是约束后的解$-$左区间的解(因为在一个区间内右区间一定受左区间约束),剩下的一定是约束后的右区间的解。
单点修改时,维护$maxv$时维护区间的$cnt$(这里因为数值的修改包括在区间中,要对$cnt$进行修改)
也就是:
cnt[o] = cnt[lson] + pushup(rson, mid+1, r, maxv[lson]);
于是问题就解决了。
复杂度分析:单点修改$O(log n)$,一次$ ext{pushup}$需要$O(log n)$,所以一次的复杂度为$O(log^2n)$。
1 #include <bits/stdc++.h> 2 3 using namespace std; 4 5 #define re register 6 #define rep(i, a, b) for (re int i = a; i <= b; ++i) 7 #define repd(i, a, b) for (re int i = a; i >= b; --i) 8 #define For(i, a, b, s) for (re int i = a; i <= b; s) 9 #define maxx(a, b) a = max(a, b) 10 #define minn(a, b) a = min(a, b) 11 #define LL long long 12 #define INF (1 << 30) 13 14 inline int read() { 15 int w = 0, f = 1; char c = getchar(); 16 while (!isdigit(c)) f = c == '-' ? -1 : f, c = getchar(); 17 while (isdigit(c)) w = (w << 3) + (w << 1) + (c ^ '0'), c = getchar(); 18 return w * f; 19 } 20 21 const int maxn = 1e5 + 5, N = 100000; 22 23 double a[maxn]; 24 25 struct SegT { 26 #define lson (o << 1) 27 #define rson (o << 1 | 1) 28 double maxv[maxn << 2]; 29 int cnt[maxn << 2]; 30 void build(int o, int l, int r) { 31 if (l == r) { cnt[o] = 1; return; } 32 int mid = (l + r) >> 1; 33 build(lson, l, mid); build(rson, mid+1, r); 34 } 35 void maintain(int o) { maxv[o] = max(maxv[lson], maxv[rson]); } 36 int pushup(int o, int l, int r, double d) { 37 if (l == r) return maxv[o]-d > 1e-10 ? 1: 0; 38 int mid = (l + r) >> 1; 39 if (maxv[lson]-d > 1e-10) { // l > o 40 return pushup(lson, l, mid, d) + cnt[o] - cnt[lson]; 41 } else { // l <= o 42 return pushup(rson, mid+1, r, d); 43 } 44 } 45 void modify(int o, int l, int r, int x, int y) { 46 if (l == r) { 47 maxv[o] = (double)y / x; 48 cnt[o] = y ? 1 : 0; 49 return; 50 } 51 int mid = (l + r) >> 1; 52 if (x <= mid) modify(lson, l, mid, x, y); else modify(rson, mid+1, r, x, y); 53 maintain(o); 54 cnt[o] = cnt[lson] + pushup(rson, mid+1, r, maxv[lson]); 55 } 56 } T; 57 58 int n, m; 59 int x, y; 60 61 int main() { 62 n = read(); m = read(); 63 rep(i, 1, m) { 64 x = read(), y = read(); 65 T.modify(1, 1, N, x, y); 66 printf("%d ", T.cnt[1]); 67 } 68 return 0; 69 }