227. Mock Hanoi Tower by Stacks【easy】

In the classic problem of Towers of Hanoi, you have 3 towers and N disks of different sizes which can slide onto any tower. The puzzle starts with disks sorted in ascending order of size from top to bottom (i.e., each disk sits on top of an even larger one). You have the following constraints:

1. Only one disk can be moved at a time.
2. A disk is slid off the top of one tower onto the next tower.
3. A disk can only be placed on the top of a larger disk.

Write a program to move the disks from the first tower to the last using stacks.

解法一：

class Tower {
public:
    // create three towers (i from 0 to 2)
    Tower(int i) {}
    
    // Add a disk into this tower
    void add(int d) {
        if (!disks.empty() && disks.top() <= d) {
            printf("Error placing disk %d", d);
        } else {
            disks.push(d);
        }
    }
    
    // @param t a tower
    // Move the top disk of this tower to the top of t.
    void moveTopTo(Tower &t) {
        // Write your code here
        int top = disks.top();
        disks.pop();
        t.add(top);
    }
    
    // @param n an integer
    // @param destination a tower
    // @param buffer a tower
    // Move n Disks from this tower to destination by buffer tower
    void moveDisks(int n, Tower &destination, Tower &buffer) {
        // Write your code here
        if (n > 0) {
            moveDisks(n - 1, buffer, destination);
            moveTopTo(destination);
            buffer.moveDisks(n - 1, destination, *this);
        }
    }

    stack<int> getDisks() {
        return disks;
    }

private:
    stack<int> disks;
};

/**
 * Your Tower object will be instantiated and called as such:
 * vector<Tower> towers;
 * for (int i = 0; i < 3; i++) towers.push_back(Tower(i));
 * for (int i = n - 1; i >= 0; i--) towers[0].add(i);
 * towers[0].moveDisks(n, towers[2], towers[1]);
 * print towers[0], towers[1], towers[2]
*/

思路：

add：如果栈顶元素大于要加入元素，则加入

moveTopTo：如果目标柱子的栈顶元素大于要移动元素，则加入目标柱子栈

moveDisks：如果要移动盘子数量n大于0，则递归地将n－1个盘子通过目标柱子移到buffer柱子，然后将最后一个盘子移到目标柱子，最后再递归地将buffer柱子上的n－1个盘子通过原来的柱子移到目标柱子

补充：

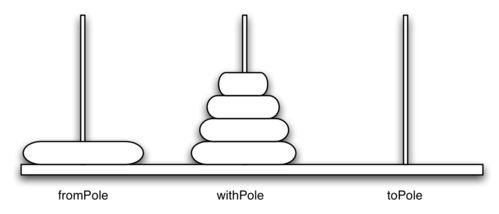
The pic above shows an example of a configuration of disks in the middle of a move from the first peg to the third. Notice that, as the rules specify, the disks on each peg are stacked so that smaller disks are always on top of the larger disks. If you have not tried to solve this puzzle before, you should try it now. You do not need fancy disks and poles–a pile of books or pieces of paper will work.

How do we go about solving this problem recursively? How would you go about solving this problem at all? What is our base case? Let’s think about this problem from the bottom up. Suppose you have a tower of five disks, originally on peg one. If you already knew how to move a tower of four disks to peg two, you could then easily move the bottom disk to peg three, and then move the tower of four from peg two to peg three. But what if you do not know how to move a tower of height four? Suppose that you knew how to move a tower of height three to peg three; then it would be easy to move the fourth disk to peg two and move the three from peg three on top of it. But what if you do not know how to move a tower of three? How about moving a tower of two disks to peg two and then moving the third disk to peg three, and then moving the tower of height two on top of it? But what if you still do not know how to do this? Surely you would agree that moving a single disk to peg three is easy enough, trivial you might even say. This sounds like a base case in the making.

Here is a high-level outline of how to move a tower from the starting pole, to the goal pole, using an intermediate pole:

1. Move a tower of height-1 to an intermediate pole, using the final pole.
2. Move the remaining disk to the final pole.
3. Move the tower of height-1 from the intermediate pole to the final pole using the original pole.

As long as we always obey the rule that the larger disks remain on the bottom of the stack, we can use the three steps above recursively, treating any larger disks as though they were not even there. The only thing missing from the outline above is the identification of a base case. The simplest Tower of Hanoi problem is a tower of one disk. In this case, we need move only a single disk to its final destination. A tower of one disk will be our base case. In addition, the steps outlined above move us toward the base case by reducing the height of the tower in steps 1 and 3. The code following shows the Python code to solve the Tower of Hanoi puzzle.

def moveTower(height,fromPole, toPole, withPole):
    if height >= 1:
        moveTower(height-1,fromPole,withPole,toPole)
        moveDisk(fromPole,toPole)
        moveTower(height-1,withPole,toPole,fromPole)

Notice that the code above is almost identical to the English description. The key to the simplicity of the algorithm is that we make two different recursive calls, one on line 3 and a second on line 5. On line 3 we move all but the bottom disk on the initial tower to an intermediate pole. The next line simply moves the bottom disk to its final resting place. Then on line 5 we move the tower from the intermediate pole to the top of the largest disk. The base case is detected when the tower height is 0; in this case there is nothing to do, so the moveTower function simply returns. The important thing to remember about handling the base case this way is that simply returning from moveTower is what finally allows the moveDisk function to be called.

参考自：https://interactivepython.org/runestone/static/pythonds/Recursion/TowerofHanoi.html