写在前面
这几天一直在做 (Tarjan) 算法,也恰好遇上这一个题目,那就做一做吧,看了一些题解也不多,就交一下
题面大意
和3469雷同了,这里也还是说一下吧,给定一张无向图,求每个点被封锁之后有多少个有序点对 ((x,y) (x ot =y,1<=x,y<=n)) 满足 (x) 无法到达(y) ,
思路
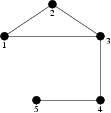
然后手动模拟一下敲点,把节点 (1) 敲掉,我们就可以发现 ((1,2),(2,1)……(1,5)(5,1)) 这8个有序数对是无法相互到达的,所以我们可以得出一个结论,当节点 (x) 不是一个割点的时候,我们删去它,它贡献的有序点对数为 (2 imes(n - 1)) ,(n-1)就是除了自己,都不能到达了,但是这是一个有序数对,无向图,所以要 ( imes 2)
当我们敲掉节点 (3) 的时候,我们也尝试用上面的,首先就是到达节点 (3) 的有序数对都不能到达了,那么就是 (2 imes (5 - 1)) 了,但是我们发现,由于节点 (3) 是一个割点,我们把它删除以后,$(1,4) , (4,1)……(2 , 5) (5,2) $,都不能到达了,式子化简出来就是这么式子
什么意思,就是(top)删去节点(3)之后,上面的总共几个节点,对应着上面的(1,2),(back)就是下面几个节点,对应着上面的(4,5),然后这个式子因为里面是(1)的总和,所以,我们就可以提出来,也就是
(top,back)还是上面的意思。
综上,我们就找出来了这几个点的情况,
当它是割点的时候,贡献是它的子树的大小的乘积
当它不是割点的时候,贡献是 ((n-1) imes 2)
其实这个题还可以加强一下,是图不连通的情况,那么不是割点的节点的贡献就变成 ((len_i - 1) imes 2) ,其中 (len_i) 表示的是节点 (i) 所处的连通块的大小。
( ext{code})
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <queue>
#include <set>
#include <stack>
#define int long long
using namespace std ;
const int kmaxn = 5e6 + 10 ;
inline int read()
{
int x = 0 , f = 1 ; char ch = getchar() ;
while(!isdigit(ch)) { if(ch == '-') f = - 1 ; ch = getchar() ; }
while( isdigit(ch)) { x = x * 10 + ch - '0' ; ch = getchar() ; }
return x * f ;
}
struct node
{
int nxt , v , u , val ;
}e[kmaxn << 1] ;
int tot , h[kmaxn << 1] ;
void add(int u , int v )
{
e[++tot].nxt = h[u] ;
e[tot].u = u ;
e[tot].v = v ;
h[u] = tot ;
}
int sum , cnt , n , m ;
int dfn[kmaxn << 1] , low[kmaxn] , cut[kmaxn] , size[kmaxn] , ans[kmaxn] ;
void tarjan(int u, int fa)
{
low[u] = dfn[u] = ++cnt;
int child = 0 ;
int sum = 0 ;
size[u] = 1 ;
for (int i = h[u]; i; i = e[i].nxt)
{
int v = e[i].v;
if (!dfn[v])
{
tarjan(v, u) ;
size[u] += size[v] ;
low[u] = min(low[u], low[v]);
if(low[v] >= dfn[u] )
{
cut[u] = 1;
sum += size[v];
ans[u] += size[v] * ( n - size[v] ) ;
if(child >= 2 || u != fa) cut[u] = 1;
}
if(u == fa) child ++;
}
else low[u] = min(low[u], dfn[v]);
}
if(!cut[u]) ans[u] = (n - 1) * 2 ;//该点是割点
else ans[u] += (n - sum - 1) * (sum + 1) + (n - 1 ) ;
}
signed main()
{
n = read() , m = read() ;
for(int i = 1 ; i <= m ; i++)
{
int u = read() , v = read() ;
add( u , v ) ;
add( v , u ) ;
}
for(int i = 1 ; i <= n ; i++)
{
if(!dfn[i])
{
tarjan(i , i) ;
}
}
for(int i = 1 ; i <= n ; i++)
{
printf("%lld
" , ans[i]);
}
return 0 ;
}