11.1 BFS算法的实验范例
§6.1 概述
图
图结构是描述和解决实际应用问题的一种基本而有力的工具。所谓的图(graph),可定义为G = (V, E)。其中,集合V中的元素称作顶点(vertex);集合E中的元素分别对应于V中的某一对顶点(u, v),表示它们之间存在某种关系,故亦称作边(edge) ①。一种直观显示图结构的方法是,用小圆圈或小方块代表顶点,用联接于其间的直线段或曲线弧表示对应的边。 从计算的需求出发,我们约定V和E均为有限集,通常将其规模分别记n = |V|和e = |E|。
无向图、有向图及混合图
若边(u, v)所对应顶点u和v的次序无所谓,则称作无向边(undirected edge),例如表示同学关系的边。反之若u和v不对等,则称(u, v)为有向边(directed edge),例如描述企业与银行之间的借贷关系,或者程序之间的相互调用关系的边。
在某些文献中,顶点也称作节点(node),边亦称作弧(arc),本章则统一称作顶点和边。
如此,无向边(u, v)也可记作(v, u),而有向的(u, v)和(v, u)则不可混淆。这里约定,有向边(u, v)从u指向v,其中u称作该边的起点(origin)或尾顶点(tail),而v称作该边的终点(destination)或头顶点(head)。
若E中各边均无方向,则G称作无向图(undirected graph,简称undigraph)。例如在描述影视演员相互合作关系的图G中,若演员u和v若曾经共同出演过至少一部影片,则在他(她) 们之间引入一条边(u, v)。反之,若E中只含有向边,则G称作有向图(directed graph,简称 digraph)。例如在C++类的派生关系图中,从顶点u指向顶点v的有向边,意味着类u派生自类v。特别地,若E同时包含无向边和有向边,则G称作混合图(mixed graph)。例如在北京市内交通图中,有些道路是双行的,另一些是单行的,对应地可分别描述为无向边和有向边。
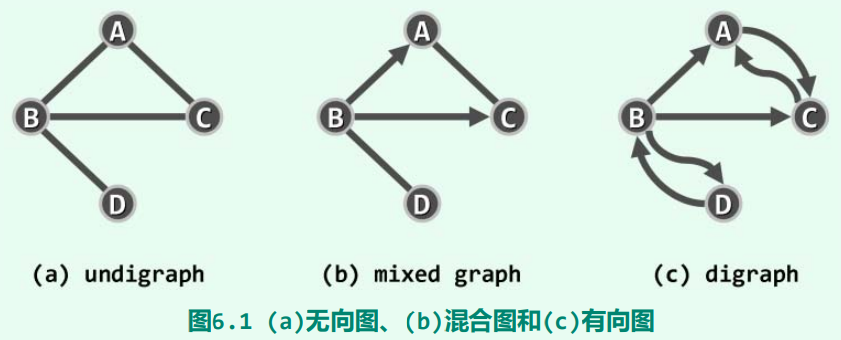
相对而言,有向图的通用性更强,因为无向图和混合图都可转化为有向图————如图6.1所示, 每条无向边(u, v)都可等效地替换为对称的一对有向边(u, v)和(v, u)。因此,本章将主要针对有向图,介绍图结构及其算法的具体实现。
度
对于任何边e = (u, v),称顶点u和v彼此邻接(adjacent),互为邻居;而它们都与边e彼此关联(incident)。在无向图中,与顶点v关联的边数,称作v的度数(degree),记作deg(v)。以图6.1(a)为例,顶点{ A, B, C, D }的度数为{ 2, 3, 2, 1 }。
对于有向边e = (u, v),e称作u的出边(outgoing edge)、v的入边(incoming edge)。v的出边总数称作其出度(out-degree),记作outdeg(v);入边总数称作其入度(in-degree),记作indeg(v)。在图6.1(c)中,各顶点的出度为{ 1, 3, 1, 1 },入度为{ 2, 1, 2, 1 }。
简单图
联接于同一顶点之间的边,称作自环(self-loop)。在某些特定的应用中,这类边可能的确具有意义————比如在城市交通图中,沿着某条街道,有可能不需经过任何交叉路口即可直接返回原处。不含任何自环的图称作简单图(simple graph),也是本书主要讨论的对象。
通路与环路
所谓路径或通路(path),就是由m + 1个顶点与m条边交替而成的一个序列:π = { v0, e1, v1, e2, v2, ..., em, vm }
且对任何0 < i <= m都有ei = (vi-1, vi)。也就是说,这些边依次地首尾相联。其中沿途边的总数m,亦称作通路的长度,记作|π| = m。
为简化描述,也可依次给出通路沿途的各个顶点,而省略联接于其间的边,即表示为: π = { v0, v1, v2, ..., vm }
图6.2(a)中的{ C, A, B, A, D },即是从顶点C到D的一条通路,其长度为4。可见,尽管通路上的边必须互异,但顶点却可能重复。沿途顶点互异的通路,称作简单通路(simple path)。在图6.2(b)中,{ C, A, D, B }即 是从顶点C到B的一条简单通路,其长度为3。

特别地,对于长度m >= 1的通路π,若起止顶点相同(即v0 = vm),则称作环路(cycle),其长度也取作沿途边的总数。图6.3(a)中,{ C, A, B, A, D, B, C }即是一条环路,其长度为 6。反之,不含任何环路的有向图,称作有向无环图(directed acyclic graph, DAG)。
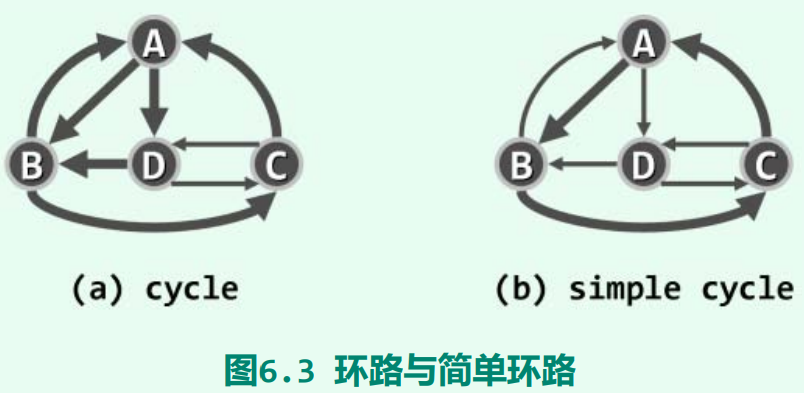
同样,尽管环路上的各边必须互异,但顶点却也可能重复。反之若沿途除v0 = vm外所有顶点均互异,则称作简单环路(simple cycle)。例如,图6.3(b)中的{ C, A, B, C }即是一条简单环路,其长度为3。特别地,经过图中各边一次且恰好一次的环路,称作欧拉环路 (Eulerian tour)————当然,其长度也恰好等于图中边的总数e。
图6.4(a)中的{ C, A, B, A, D, C, D, B, C }即是一条欧拉环路,其长度为8。对偶地,经过图中各顶点一次且恰好一次的环路,称作哈密尔顿环路(Hamiltonian tour),其长度亦等于构成环路的边数。图6.4(b)中,{ C, A, D, B, C }即是一条长度为4的哈密尔顿环路。

带权网络
图不仅需要表示顶点之间是否存在某种关系,有时还需要表示这一关系的具体细节。以铁路运输为例,可以用顶点表示城市,用顶点之间的联边,表示对应的城市之间是否有客运铁路联接;同时,往往还需要记录各段铁路的长度、承运能力,以及运输成本等信息。
为适应这类应用要求,需通过一个权值函数,为每一边e指定一个权重(weight),比如wt(e) 即为边e的权重。各边均带有权重的图,称作带权图(weighted graph)或带权网络(weighted network),有时也简称网络(network),记作G(V, E, wt())。
复杂度
与其它算法一样,图算法也需要就时间性能和空间性能,进行分析和比较。相应地,问题的输入规模,也应该以顶点数与边数的总和(n + e)来度量。不难看出,无论顶点多少,边数都有可能为0。那么反过来,在包含n个顶点的图中,至多可能包含多少条边呢?
对于无向图,每一对顶点至多贡献一条边,故总共不超过n(n - 1)/2条边,且这个上界由完全图达到。对于有向图,每一对顶点都可能贡献(互逆的)两条边,因此至多可有n(n - 1) 条边。总而言之,必有e = O(n^2 )。
§6.2 抽象数据类型
6.2.1 操作接口
作为抽象数据类型,图支持的操作接口分为边和顶点两类,分列于表6.1和表6.2。

6.2.2 Graph模板类
代码6.1以抽象模板类的形式,给出了图ADT的具体定义。
仍为简化起见,这里直接开放了变量n和e。除以上所列的操作接口,这里还明确定义了顶点和边可能处于的若干状态,并通过内部接口reset()复位顶点和边的状态。
图的部分基本算法在此也以操作接口的形式供外部用户直接使用,比如广度优先搜索、深度优先搜索、双连通分量分解、最小支撑树、最短路径等。为求解更多的具体应用问题,读者可照此模式,独立地补充相应的算法。
就功能而言,这些算法均超脱于图结构的具体实现方式,借助统一的顶点和边ADT操作接口直接编写。尽管如此,正如以下即将看到的,图算法的时间、空间性能,却与图结构的具体实现方式紧密相关,在这方面的理解深度,也将反映和决定我们对图结构的驾驭与运用能力。
§6.3 邻接矩阵
6.3.1 原理
邻接矩阵(adjacency matrix)是图ADT最基本的实现方式,使用方阵A[n][n]表示由n个顶点构成的图,其中每个单元,各自负责描述一对顶点之间可能存在的邻接关系,故此得名。
对于无权图,存在 (不存在)从顶点u到v的边,当且仅当A[u][v] = 1(0)。图6.5(a)和(b)即为无向图和有向图的邻接矩阵实例。这一表示方式,不难推广至带权网络。此时如图(c)所示,矩阵各单元可从布尔型改为整型或浮点型,记录所对应边的权重。对于不存在的边,通常统一取值为∞或0。