状态压缩DP
旅行商问题
- 问题描述:给定一个n个顶点组成的带权有向图的距离矩阵d(i,j),要求从顶点0出发,经过每个顶点恰好一次后再回到顶点0.问所经过的边的总权重的最小值是多少?
- 限制条件:
2≤n≤15
0≤d(i,j)≤1000 - 分析:著名的旅行商问题(TSP, Traveling Salesman Problem)。TSP问题是NP困难的,没有已知的多项式时间的高效算法。
所有可能的路线共有(n-1)!种,无法试遍每一种情况。
对于这个问题,我们可以使用DP。先写递推式,假设现在已经访问过的顶点的集合(起点0当作还未访问过的顶点)为S,当前所在的顶点为v,用dp[S][v]表示从v出发访问剩余的所有顶点,最终回到顶点0的路径的权重总和的最小值。由于从v出发可以移动到任意的一个节点u∉S,因此有如下递推式:
dp[V][0]=0
dp[S][v]=min{dp[ S∪{u} ] [u] + d(v,u) |u∉S}
我们只要按照这个递推式进行计算就可以了,由于在这个递推式中有一个下标是集合而不是普通的整数,因此需要稍加处理。首先我们试着使用记忆化搜索求解,虽然有一个下标不是整数,但我们可以把它编码成一个整数,或者个它定义一个全序关系并用二叉搜索树存储,从而可以使用记忆化搜索来求解。特别地,对于集合我们可以把每一个元素的选取与否对应到一个二进制位里,从而把状态压缩成一个整数,大大方便了计算和维护。 - 代码:
 TSP
TSP1 #include <cstdio> 2 #include <cstdio> 3 #include <cctype> 4 #include <cstring> 5 #define number s-'0' 6 7 using namespace std; 8 9 const int MAX_N=20; 10 const int INF=0x3f3f3f3f; 11 int n,m; 12 int d[MAX_N][MAX_N]; 13 int dp[1<<MAX_N][MAX_N]; 14 int pre[MAX_N]; 15 16 void read(int &x) 17 { 18 char s; 19 x=0; 20 bool flag=0; 21 while(!isdigit(s=getchar())) 22 (s=='-')&&(flag=true); 23 for(x=number;isdigit(s=getchar());x=x*10+number); 24 (flag)&&(x=-x); 25 } 26 27 void write(int x) 28 { 29 if(x<0) 30 { 31 putchar('-'); 32 x=-x; 33 } 34 if(x>9) write(x/10); 35 putchar(x%10+'0'); 36 } 37 38 int rec(int S, int v); 39 40 int main() 41 { 42 read(n);read(m); 43 memset(d, 0x3f, sizeof(d)); 44 for (int i=0; i<n; i++) i[i[d]]=0; 45 for (int i=0; i<m; i++) 46 { 47 int x,y,z; 48 read(x);read(y);read(z); 49 d[x][y]=z; 50 } 51 memset(dp, -1, sizeof(dp)); 52 write(rec(0,0)); 53 putchar(' '); 54 } 55 56 int min(int x, int y) 57 { 58 if (x<=y) return x; 59 return y; 60 } 61 62 int rec(int S, int v) 63 { 64 if (dp[S][v]>=0) return dp[S][v]; 65 if (S==(1<<n)-1 && v==0) return dp[S][v]=0; 66 int res=INF; 67 for (int u=0; u<n; u++) 68 { 69 if (!(S>>u&1)) res=min(res, rec(S|1<<u, u)+d[v][u]); 70 } 71 return dp[S][v]=res; 72 }
这样,就可以在O(2nn2)的时间内完成计算。对于不是整数的情况,很多时候很难确定一个合适的递推顺序,因此使用记忆化搜索可以避免这个问题。
不过,在这个问题中,对于任意两个整数i和j,如果它们对应的集合满足S(i)⊆S(j),就有i≤j,因此还可通过循环求出答案: TSP'
TSP'1 #include <cstdio> 2 #include <cstdio> 3 #include <cctype> 4 #include <cstring> 5 #define number s-'0' 6 7 using namespace std; 8 9 const int MAX_N=20; 10 const int INF=0x3f3f3f3f; 11 int n,m; 12 int d[MAX_N][MAX_N]; 13 int dp[1<<MAX_N][MAX_N]; 14 int pre[MAX_N]; 15 16 void read(int &x) 17 { 18 char s; 19 x=0; 20 bool flag=0; 21 while(!isdigit(s=getchar())) 22 (s=='-')&&(flag=true); 23 for(x=number;isdigit(s=getchar());x=x*10+number); 24 (flag)&&(x=-x); 25 } 26 27 void write(int x) 28 { 29 if(x<0) 30 { 31 putchar('-'); 32 x=-x; 33 } 34 if(x>9) write(x/10); 35 putchar(x%10+'0'); 36 } 37 38 int min(int x, int y) 39 { 40 if (x<=y) return x; 41 return y; 42 } 43 44 int main() 45 { 46 read(n);read(m); 47 memset(d, 0x3f, sizeof(d)); 48 for (int i=0; i<n; i++) i[i[d]]=0; 49 for (int i=0; i<m; i++) 50 { 51 int x,y,z; 52 read(x);read(y);read(z); 53 d[x][y]=z; 54 } 55 memset(dp, 0x3f, sizeof(dp)); 56 dp[(1<<n)-1][0]=0; 57 for (int S=(1<<n)-2; S>=0; S--) 58 { 59 for (int v=0; v<n; v++) 60 { 61 for (int u=0; u<n; u++) 62 { 63 if (!(S>>u&1)) 64 dp[S][v]=min(dp[S][v], dp[S|1<<u][u]+d[v][u]); 65 } 66 } 67 } 68 write(0[0[dp]]); 69 putchar(' '); 70 }
像这样针对集合的DP我们一般叫状态压缩DP
Traveling by Stagecoach(POJ 2686)
- 原题如下:
Traveling by Stagecoach
Time Limit: 2000MS Memory Limit: 65536K Total Submissions: 4482 Accepted: 1847 Special Judge Description
Once upon a time, there was a traveler.
He plans to travel using stagecoaches (horse wagons). His starting point and destination are fixed, but he cannot determine his route. Your job in this problem is to write a program which determines the route for him.
There are several cities in the country, and a road network connecting them. If there is a road between two cities, one can travel by a stagecoach from one of them to the other. A coach ticket is needed for a coach ride. The number of horses is specified in each of the tickets. Of course, with more horses, the coach runs faster.
At the starting point, the traveler has a number of coach tickets. By considering these tickets and the information on the road network, you should find the best possible route that takes him to the destination in the shortest time. The usage of coach tickets should be taken into account.
The following conditions are assumed.
- A coach ride takes the traveler from one city to another directly connected by a road. In other words, on each arrival to a city, he must change the coach.
- Only one ticket can be used for a coach ride between two cities directly connected by a road.
- Each ticket can be used only once.
- The time needed for a coach ride is the distance between two cities divided by the number of horses.
- The time needed for the coach change should be ignored.
Input
The input consists of multiple datasets, each in the following format. The last dataset is followed by a line containing five zeros (separated by a space).
n m p a b
t1 t2 ... tn
x1 y1 z1
x2 y2 z2
...
xp yp zp
Every input item in a dataset is a non-negative integer. If a line contains two or more input items, they are separated by a space.
n is the number of coach tickets. You can assume that the number of tickets is between 1 and 8. m is the number of cities in the network. You can assume that the number of cities is between 2 and 30. p is the number of roads between cities, which may be zero.
a is the city index of the starting city. b is the city index of the destination city. a is not equal to b. You can assume that all city indices in a dataset (including the above two) are between 1 and m.
The second line of a dataset gives the details of coach tickets. ti is the number of horses specified in the i-th coach ticket (1<=i<=n). You can assume that the number of horses is between 1 and 10.
The following p lines give the details of roads between cities. The i-th road connects two cities with city indices xi and yi, and has a distance zi (1<=i<=p). You can assume that the distance is between 1 and 100.
No two roads connect the same pair of cities. A road never connects a city with itself. Each road can be traveled in both directions.Output
For each dataset in the input, one line should be output as specified below. An output line should not contain extra characters such as spaces.
If the traveler can reach the destination, the time needed for the best route (a route with the shortest time) should be printed. The answer should not have an error greater than 0.001. You may output any number of digits after the decimal point, provided that the above accuracy condition is satisfied.
If the traveler cannot reach the destination, the string "Impossible" should be printed. One cannot reach the destination either when there are no routes leading to the destination, or when the number of tickets is not sufficient. Note that the first letter of "Impossible" is in uppercase, while the other letters are in lowercase.Sample Input
3 4 3 1 4 3 1 2 1 2 10 2 3 30 3 4 20 2 4 4 2 1 3 1 2 3 3 1 3 3 4 1 2 4 2 5 2 4 3 4 1 5 5 1 2 10 2 3 10 3 4 10 1 2 0 1 2 1 8 5 10 1 5 2 7 1 8 4 5 6 3 1 2 5 2 3 4 3 4 7 4 5 3 1 3 25 2 4 23 3 5 22 1 4 45 2 5 51 1 5 99 0 0 0 0 0
Sample Output
30.000 3.667 Impossible Impossible 2.856
Hint
Since the number of digits after the decimal point is not specified, the above result is not the only solution. For example, the following result is also acceptable.
30.0
3.66667
Impossible
Impossible
2.85595 - 题解:如果把城市看作顶点,道路看作边建图,由于有车票相关的限制,无法直接使用Dijkstra算法求解。不过,这种情况下只需要把状态作为顶点,而把状态的转移看成边建图就可以很好地避免这个问题。考虑"现在在城市v,此时还剩下的车票的集合为S"这样的状态,从这个状态出发,使用一张车票i∈S移动到相邻的城市u,就相当于转移到了"在城市u,此时还剩下的车票的集合为S{i}"这个状态。把这个转移看成一条边,那么边上的花费是(v-u间道路的长度)/ti。按照上述的方法所构的图就可以用Dijkstra算法求解了。集合S使用状态压缩的方法表示就可以了。由于剩余的车票的集合S随着移动元素个数不断变小,因此这个图实际上一个DAG,计算DAG的最短路不需要是用Dijkstra算法,可以简单地通过DP求解。
- 代码:
 Traveling by Stagecoach
Traveling by Stagecoach1 #include <cstdio> 2 #include <cstdio> 3 #include <cctype> 4 #include <cstring> 5 #include <algorithm> 6 #define number s-'0' 7 8 using namespace std; 9 10 const int INF=0x3f3f3f3f; 11 const int MAX_N=10; 12 const int MAX_M=40; 13 int n,m,p,a,b; 14 int t[MAX_N]; 15 int d[MAX_M][MAX_M]; 16 double dp[1<<MAX_N][MAX_M]; 17 18 void read(int &x) 19 { 20 char s; 21 x=0; 22 bool flag=0; 23 while(!isdigit(s=getchar())) 24 (s=='-')&&(flag=true); 25 for(x=number;isdigit(s=getchar());x=x*10+number); 26 (flag)&&(x=-x); 27 } 28 29 double min(double x, double y) 30 { 31 if (x<=y) return x; 32 return y; 33 } 34 35 int main() 36 { 37 read(n);read(m);read(p);read(a);read(b); 38 while (n+m+p+a+b) 39 { 40 for (int i=0; i<n; i++) read(t[i]); 41 memset(d, -1, sizeof(d)); 42 for (int i=0; i<p; i++) 43 { 44 int x, y, z; 45 read(x);read(y);read(z); 46 x--;y--; 47 x[y[d]]=y[x[d]]=z; 48 } 49 for (int i=0; i<1<<n; i++) 50 { 51 fill(dp[i], dp[i]+m, INF); 52 } 53 dp[(1<<n)-1][a-1]=0; 54 double res=INF; 55 for (int S=(1<<n)-1; S>=0; S--) 56 { 57 res=min(res, dp[S][b-1]); 58 for (int v=0; v<m; v++) 59 { 60 for (int i=0; i<n; i++) 61 { 62 if ((S>>i)&1) 63 { 64 for (int u=0; u<m; u++) 65 { 66 if (d[v][u]>=0) 67 { 68 dp[S&~(1<<i)][u]=min(dp[S&~(1<<i)][u],dp[S][v]+d[v][u]/(double)t[i]); 69 } 70 } 71 } 72 } 73 } 74 } 75 if (res==INF) puts("Impossible"); 76 else printf("%.3f ", res); 77 read(n);read(m);read(p);read(a);read(b); 78 } 79 }
铺砖问题
- 问题描述:给定n*m的格子,每个格子被染成黑色或者白色(.表示白色,x表示黑色)。现在要用1*2的砖块覆盖这些格子,要求块与块之间互相不重叠,且覆盖了所有白色的格子,但不覆盖任意一个黑色格子。求一共有多少种覆盖方法。输出方案数对M取余后的结果。
- 限制条件:
1≤n≤15
1≤m≤15
2≤M≤109 - 分析:首先考虑枚举所有的解为了不重复统计,每次从最左上方的空格处开始放置:
 枚举(搜索)
枚举(搜索)1 #include <cstdio> 2 #include <cstring> 3 4 using namespace std; 5 6 const int MAX_N=15; 7 const int MAX_M=15; 8 const int M=100007; 9 int n,m; 10 bool color[MAX_N][MAX_M]; 11 12 int rec(int i, int j, bool used[MAX_N][MAX_M]); 13 14 int main(int argc, char * argv[]) 15 { 16 scanf("%d %d ", &n, &m); 17 for (int i=0; i<n; i++) 18 { 19 char c; 20 for (int j=0; j<m; j++) 21 { 22 scanf("%c", &c); 23 if (c=='.') color[i][j]=false; 24 else color[i][j]=true; 25 } 26 getchar(); 27 } 28 bool used[MAX_N][MAX_M]; 29 memset(used, 0, sizeof(used)); 30 printf("%d ", rec(0, 0, used)); 31 } 32 33 int rec(int i, int j, bool used[MAX_N][MAX_M]) 34 { 35 if (j==m) return rec(i+1, 0, used); 36 if (i==n) return 1; 37 if (used[i][j] || color[i][j]) return rec(i, j+1, used); 38 int res=0; 39 used[i][j]=true; 40 if (j+1<m && !used[i][j+1] && !color[i][j+1]) 41 { 42 used[i][j+1]=true; 43 res+=rec(i, j+1, used); 44 used[i][j+1]=false; 45 } 46 if (i+1<n && !used[i+1][j] && !color[i+1][j]) 47 { 48 used[i+1][j]=true; 49 res+=rec(i, j+1, used); 50 used[i+1][j]=false; 51 } 52 used[i][j]=false; 53 return res%M; 54 }
这个方法效率不足,且递归函数的参数共有n*m*2n*m种可能,无法使用记忆化搜索。
自习思考之后会发现,实际上参数并没有那么多种可能,首先,由于黑色的格子不能被覆盖,因此used里对应的位置总是false,对于白色的格子,如果现在要在(i,j)位置上放置砖块,那么由于总是从最左上方的可放的格子开始放置,因此对于(i',j')<(i,j)(按字典序比较)的(i',j')总有used[i'][j']=true成立,此外,由于砖块的大小为1*2,因此对于每一列j'在满足(i',j')≥(i,j)的所有i'中,除了最小的i'之外都满足used[i'][j']=false。因此,不确定的只有每一列里还没有查询的格子中最上面的一个,共m个。从而可以把这m个格子通过状态压缩编码进行记忆化搜索,复杂度为O(n*m*2m)。 - 代码:
 状态压缩DP
状态压缩DP1 #include <cstdio> 2 #include <cstring> 3 4 using namespace std; 5 6 const int MAX_N=15; 7 const int MAX_M=15; 8 const int M=100007; 9 int n,m; 10 bool color[MAX_N][MAX_M]; 11 int dp[2][1<<MAX_M]; 12 13 void swap(int *a[], int *b[]) 14 { 15 int *t; 16 t=*a; 17 *a=*b; 18 *b=t; 19 } 20 21 int main(int argc, char * argv[]) 22 { 23 scanf("%d %d ", &n, &m); 24 for (int i=0; i<n; i++) 25 { 26 char c; 27 for (int j=0; j<m; j++) 28 { 29 scanf("%c", &c); 30 if (c=='.') color[i][j]=false; 31 else color[i][j]=true; 32 } 33 getchar(); 34 } 35 int *crt=dp[0], *next=dp[1]; 36 crt[0]=1; 37 for (int i=n-1; i>=0; i--) 38 { 39 for (int j=m-1; j>=0; j--) 40 { 41 for (int used=0; used<1<<m; used++) 42 { 43 if (used>>j&1 || color[i][j]) 44 { 45 next[used]=crt[used & ~(1<<j)]; 46 } 47 else 48 { 49 int res=0; 50 if (j+1<m && !(used>>(j+1)&1) && !color[i][j+1]) 51 { 52 res+=crt[used | 1 << (j+1)]; 53 } 54 if (i+1<n && !color[i+1][j]) 55 { 56 res+=crt[used | 1 << j]; 57 } 58 next[used]=res%M; 59 } 60 } 61 swap(&crt, &next); 62 } 63 } 64 printf("%d ", crt[0]); 65 }
上面的铺砖方案,用图论的语言来说就是一个完美匹配。平面图的完美匹配的个数可以在多项式时间内求解。
矩阵的幂
斐波那契数列
- 问题描述:F0=0 F1=1 Fn+2=Fn+1+Fn,求第n项的值对104取余后的结果
- 限制条件:0≤n≤1016
- 分析:逐项计算递推式复杂度O(n),效率太低,如果求出通项:Fn=(1/√5){[(1+√5)/2]n-[(1-√5)/2]n},由于式中包含无理数,无法简单求得模104之后的结果。况且,一些问题很难求得通项公式。这些情况都可以不求出通项公式,而用矩阵高效地求出第n项的值。
把斐波那契数列表示成矩阵就得到了下面的式子: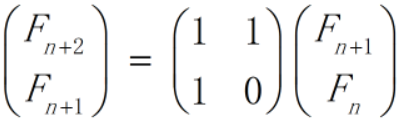
记这个矩阵为A,则有
因此只要求出An就可以求出Fn了。An用快速幂运算,在O(logn)时间里求出第n项的值。 - 代码:
 Fabnacci
Fabnacci1 #include <cstdio> 2 #include <cstring> 3 #include <vector> 4 5 using namespace std; 6 7 typedef vector<int> vec; 8 typedef vector<vec> mat; 9 long long n; 10 const int M=100007; 11 12 mat mul(mat &A, mat &B) 13 { 14 mat C(A.size(), vec(B[0].size())); 15 for (int i=0; i<A.size(); i++) 16 { 17 for (int k=0; k<B.size(); k++) 18 { 19 for (int j=0; j<B[0].size(); j++) 20 { 21 C[i][j]=(C[i][j]+A[i][k]*B[k][j])%M; 22 } 23 } 24 } 25 return C; 26 } 27 28 mat pow(mat A, long long n) 29 { 30 mat B(A.size(), vec(A.size())); 31 for (int i=0; i<A.size(); i++) 32 { 33 B[i][i]=1; 34 } 35 while (n>0) 36 { 37 if (n&1) B=mul(B, A); 38 A=mul(A, A); 39 n>>=1; 40 } 41 return B; 42 } 43 44 int main(int argc, char * argv[]) 45 { 46 scanf("%d", &n); 47 mat A(2, vec(2)); 48 A[0][0]=1;A[0][1]=1; 49 A[1][0]=1;A[1][1]=0; 50 A=pow(A,n); 51 printf("%d ", A[1][0]); 52 }
-
更一般地,对于m项递推式,如果记递推式为
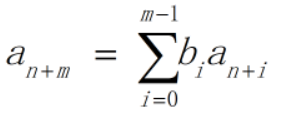
则可以把递推式写成如下矩阵形式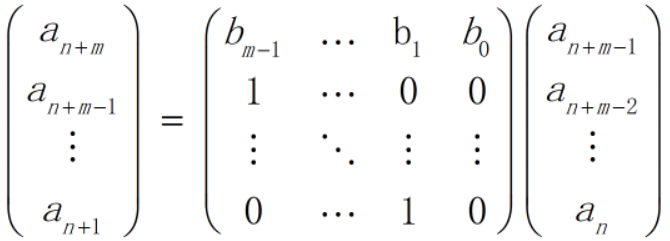
通过计算这个矩阵的n次幂,就可以在O(m3logn)的时间内计算出第n项的值,不过,如果递推式里含有常数项则稍微复杂一些,需变成如下形式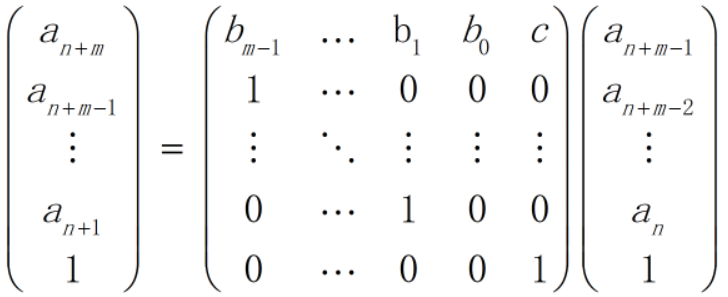
事实上,要求m项递推式的第n项的值可以不使用矩阵,而是使用初项的线性表示,用过快速幂在O(m2logn)的时间内求出答案。
Blocks(POJ 3734)
- 原题如下:
Blocks
Time Limit: 1000MS Memory Limit: 65536K Total Submissions: 8004 Accepted: 3901 Description
Panda has received an assignment of painting a line of blocks. Since Panda is such an intelligent boy, he starts to think of a math problem of painting. Suppose there are N blocks in a line and each block can be paint red, blue, green or yellow. For some myterious reasons, Panda want both the number of red blocks and green blocks to be even numbers. Under such conditions, Panda wants to know the number of different ways to paint these blocks.
Input
The first line of the input contains an integer T(1≤T≤100), the number of test cases. Each of the next T lines contains an integer N(1≤N≤10^9) indicating the number of blocks.
Output
For each test cases, output the number of ways to paint the blocks in a single line. Since the answer may be quite large, you have to module it by 10007.
Sample Input
2 1 2
Sample Output
2 6
- 题解:从最左边开始染色,设染到第i个方块为止,红绿都是偶数的方案数为ai,红绿恰有一个是偶数的方案数为bi,红绿都是奇数的方案数为ci。这样,染到第i+1个方块为止,红绿都是偶数的方案数有两种可能:①到第i个方块为止红绿都是偶数,并且第i+1个方块染成了蓝色或者黄色 ② 到第i个方块为止红绿恰有一个是奇数, 并且第i+1个方块染成了奇数个对应的那种颜色。因此有递推式ai+1=2*ai+bi,同样地,有bi+1=2*ai+2*bi+2*ci,ci+1=bi+2*ci,把ai,bi,ci的递推式用矩阵表示如下:

因此就有:
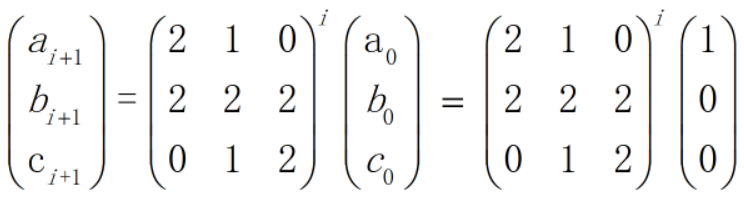
-
代码:
 Blocks
Blocks1 #include <cstdio> 2 #include <cctype> 3 #define number s-'0' 4 #include <cstring> 5 #include <vector> 6 7 using namespace std; 8 9 typedef vector<int> vec; 10 typedef vector<vec> mat; 11 12 const int M=10007; 13 int N; 14 15 void read(int &x) 16 { 17 char s; 18 x=0; 19 bool flag=0; 20 while (!isdigit(s=getchar())) 21 (s=='-')&&(flag=true); 22 for (x=number; isdigit(s=getchar());x=x*10+number); 23 (flag)&&(x=-x); 24 } 25 26 void write(int x) 27 { 28 if (x<0) 29 { 30 putchar('-'); 31 x=-x; 32 } 33 if (x>9) write(x/10); 34 putchar(x%10+'0'); 35 } 36 37 mat mul(mat &A, mat &B) 38 { 39 mat C(A.size(), vec(B[0].size())); 40 for (int i=0; i<A.size(); i++) 41 { 42 for (int j=0; j<B[0].size(); j++) 43 { 44 for (int k=0; k<B.size(); k++) 45 { 46 C[i][j]=(C[i][j]+A[i][k]*B[k][j])%M; 47 } 48 } 49 } 50 return C; 51 } 52 53 mat pow(mat A, int n) 54 { 55 mat B(A.size(), vec(A.size())); 56 for (int i=0; i<A.size(); i++) B[i][i]=1; 57 while (n>0) 58 { 59 if (n&1) B=mul(B, A); 60 A=mul(A, A); 61 n>>=1; 62 } 63 return B; 64 } 65 66 int main(int argc, char * argv[]) 67 { 68 int t; 69 read(t); 70 while (t>0) 71 { 72 t--; 73 read(N); 74 mat A(3, vec(3)); 75 A[0][0]=2;A[0][1]=1;A[0][2]=0; 76 A[1][0]=2;A[1][1]=2;A[1][2]=2; 77 A[2][0]=0;A[2][1]=1;A[2][2]=2; 78 A=pow(A, N); 79 printf("%d ",A[0][0]); 80 } 81 }
图中长度为k的路径的计数
- 问题描述:给定一个n个顶点边长为1的有向图的邻接矩阵,求这个图里长度为k的路径的总数。路径中同一条边允许通过多次。
- 限制条件:
1≤n≤100
1≤k≤109 - 题解:假设从u出发,到v的长度为k的路径的总数为Gk[u][v]。Gk=G1k。复杂度为O(n3logn)
Matrix Power Series(POJ 3233)
- 原题如下:
Matrix Power Series
Time Limit: 3000MS Memory Limit: 131072K Total Submissions: 28039 Accepted: 11438 Description
Given a n × n matrix A and a positive integer k, find the sum S = A + A2 + A3 + … + Ak.
Input
The input contains exactly one test case. The first line of input contains three positive integers n (n ≤ 30), k (k ≤ 109) and m (m < 104). Then follow n lines each containing n nonnegative integers below 32,768, giving A’s elements in row-major order.
Output
Output the elements of S modulo m in the same way as A is given.
Sample Input
2 2 4 0 1 1 1
Sample Output
1 2 2 3
- 题解:构造矩阵:
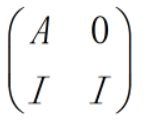
此时,令Sk=I+A+…+Ak-1,则有:
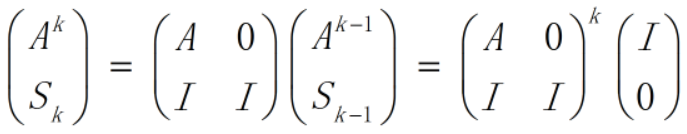
通过计算这个矩阵的k次幂,就可求出A的累乘和,时间复杂度为O(n3logk) - 代码:
 Matrix Power Series
Matrix Power Series1 #include <cstdio> 2 #include <cctype> 3 #define number s-'0' 4 #include <cstring> 5 #include <vector> 6 7 using namespace std; 8 9 typedef vector<int> vec; 10 typedef vector<vec> mat; 11 12 int n,k,m; 13 mat A; 14 15 void read(int &x) 16 { 17 char s; 18 x=0; 19 bool flag=0; 20 while (!isdigit(s=getchar())) 21 (s=='-')&&(flag=true); 22 for (x=number; isdigit(s=getchar());x=x*10+number); 23 (flag)&&(x=-x); 24 } 25 26 void write(int x) 27 { 28 if (x<0) 29 { 30 putchar('-'); 31 x=-x; 32 } 33 if (x>9) write(x/10); 34 putchar(x%10+'0'); 35 } 36 37 mat mul(mat &A, mat &B) 38 { 39 mat C(A.size(), vec(B[0].size())); 40 for (int i=0; i<A.size(); i++) 41 { 42 for (int j=0; j<B[0].size(); j++) 43 { 44 for (int k=0; k<B.size(); k++) 45 { 46 C[i][j]=(C[i][j]+A[i][k]*B[k][j])%m; 47 } 48 } 49 } 50 return C; 51 } 52 53 mat pow(mat A, int n) 54 { 55 mat B(A.size(), vec(A.size())); 56 for (int i=0; i<A.size(); i++) B[i][i]=1; 57 while (n>0) 58 { 59 if (n&1) B=mul(B, A); 60 A=mul(A, A); 61 n>>=1; 62 } 63 return B; 64 } 65 66 int main(int argc, char * argv[]) 67 { 68 read(n);read(k);read(m); 69 A=mat (n,vec(n)); 70 mat B(n*2, vec(n*2)); 71 for (int i=0; i<n; i++) 72 { 73 for (int j=0; j<n; j++) 74 { 75 read(A[i][j]); 76 B[i][j]=A[i][j]; 77 } 78 B[n+i][i]=B[n+i][n+i]=1; 79 } 80 B=pow(B,k+1); 81 for (int i=0; i<n; i++) 82 { 83 for (int j=0; j<n; j++) 84 { 85 int a=B[n+i][j]%m; 86 if (i==j) a=(a+m-1)%m; 87 printf("%d%c", a, j+1==n?' ':' '); 88 } 89 } 90 }
Minimizing maximizer(POJ 1769)
- 原题如下:
Minimizing maximizer
Time Limit: 5000MS Memory Limit: 30000K Total Submissions: 5072 Accepted: 2057 Description
The company Chris Ltd. is preparing a new sorting hardware called Maximizer. Maximizer has n inputs numbered from 1 to n. Each input represents one integer. Maximizer has one output which represents the maximum value present on Maximizer's inputs.
Maximizer is implemented as a pipeline of sorters Sorter(i1, j1), ... , Sorter(ik, jk). Each sorter has n inputs and n outputs. Sorter(i, j) sorts values on inputs i, i+1,... , j in non-decreasing order and lets the other inputs pass through unchanged. The n-th output of the last sorter is the output of the Maximizer.
An intern (a former ACM contestant) observed that some sorters could be excluded from the pipeline and Maximizer would still produce the correct result. What is the length of the shortest subsequence of the given sequence of sorters in the pipeline still producing correct results for all possible combinations of input values?
Task
Write a program that:
reads a description of a Maximizer, i.e. the initial sequence of sorters in the pipeline,
computes the length of the shortest subsequence of the initial sequence of sorters still producing correct results for all possible input data,
writes the result.Input
The first line of the input contains two integers n and m (2 <= n <= 50000, 1 <= m <= 500000) separated by a single space. Integer n is the number of inputs and integer m is the number of sorters in the pipeline. The initial sequence of sorters is described in the next m lines. The k-th of these lines contains the parameters of the k-th sorter: two integers ik and jk (1 <= ik < jk <= n) separated by a single space.Output
The output consists of only one line containing an integer equal to the length of the shortest subsequence of the initial sequence of sorters still producing correct results for all possible data.Sample Input
40 6 20 30 1 10 10 20 20 30 15 25 30 40
Sample Output
4
Hint
Huge input data, scanf is recommended. - 题解:首先,考虑在什么情况下可以正常工作,假设输入的第i个数是应该输出的最大值,此时在第一个满足sk≤i≤tk的Sorter的输出中,这个值被移动到了第tk个位置,接下去,在一个满足sk'≤tk≤tk'且k'>k的Sorter的输出中,这个值又被移动到了第tk'个。不断重复这样的操作,如果最后可以被移动到第n个,那么就表示Maximizer可以正常工作(实际上,就是要按照线段的输入顺序,将[1, n]从左到右依次覆盖,求所需线段个数的最小值)。因此只要i=1的情况可以正常工作,那么对于任意的i都可以正常工作。不妨假设第一个数是应该输出的最大值,考虑DP:
dp[i][j]:=到第i个Sorter为止,最大值被移动到第j个位置所需要的最短的子序列的长度(INF表示不存在这样的序列)
dp[0][1]=0
dp[0][j]=INF(j>1)
dp[i+1][j]=①dp[i][j] (ti ≠ j)
②min( dp[i][j] , min{dp[i][j']|si≤j'≤ti}+1 ) (ti = j)
由于这个DP的复杂度是O(nm)的,仍然无法在规定的时间内求出答案。但是对于(ti ≠ j)时有dp[i+1][j]=dp[i][j],我们可以使用同一个数组不断对自己更新:
dp[j]:=最大值被移动到第j个位置所需要的最短的子序列的长度。(INF表示不存在这样的序列)
初始化:
dp[1]=0
dp[j]=INF(j>1)
对于每个i,这样更新:
dp[ti]=min( dp[ti], min{dp[j']|si≤j'≤ti}+1 )
这样,对于每个i都只需更新一个值就可以了,但求最小值时,最坏情况下要O(n)的时间,最后复杂度还是O(nm)。如果使用线段树来维护,就可以在O(mlogn)时间内求解了。 - 代码:
 Minimizing maximizer
Minimizing maximizer1 #include <cstdio> 2 #include <cctype> 3 #include <algorithm> 4 #define number s-'0' 5 6 using namespace std; 7 8 const int INF=0x3f3f3f3f; 9 const int MAX_N=500005; 10 const int MAX_M=500005; 11 int n,m; 12 int s[MAX_M], t[MAX_M]; 13 int dp[MAX_N+1]; 14 int dat[4*MAX_N]; 15 16 void read(int &x) 17 { 18 char s; 19 bool flag=0; 20 x=0; 21 while (!isdigit(s=getchar())) 22 (s=='-')&&(flag=true); 23 for (x=number; isdigit(s=getchar());x=x*10+number); 24 (flag)&&(x=-x); 25 } 26 27 void write(int x) 28 { 29 if (x<0) 30 { 31 putchar('-'); 32 x=-x; 33 } 34 if (x>9) write(x/10); 35 putchar(x%10+'0'); 36 } 37 38 void rmq_init(int k, int l, int r); 39 void update(int u, int v, int k, int l, int r); 40 int query(int a, int b, int k, int l, int r); 41 42 int min(int x, int y) 43 { 44 if (x<y) return x; 45 return y; 46 } 47 48 int main(int argc, char * argv[]) 49 { 50 read(n);read(m); 51 for (int i=0; i<m; i++) 52 { 53 read(s[i]);read(t[i]); 54 s[i]--;t[i]--; 55 } 56 rmq_init(0, 0, n); 57 fill(dp, dp+MAX_N, INF); 58 dp[0]=0; 59 update(0, 0, 0, 0, n); 60 for (int i=0; i<m; i++) 61 { 62 int v=min(dp[t[i]], query(s[i], t[i]+1, 0, 0, n)+1); 63 dp[t[i]]=v; 64 update(t[i], v, 0, 0, n); 65 } 66 write(dp[n-1]);putchar(' '); 67 } 68 69 void rmq_init(int k, int l, int r) 70 { 71 dat[k]=INF; 72 if (r-l==1) return; 73 rmq_init(k*2+1, l, (l+r)/2); 74 rmq_init(k*2+2, (l+r)/2, r); 75 } 76 77 void update(int u, int v, int k, int l, int r) 78 { 79 if (r-l==1) 80 { 81 dat[k]=v; 82 return; 83 } 84 else 85 { 86 int m=(l+r)/2; 87 if (u<m) update(u, v, k*2+1, l, m); 88 else update(u, v, k*2+2, m, r); 89 dat[k]=min(dat[k*2+1], dat[k*2+2]); 90 } 91 } 92 93 int query(int a, int b, int k, int l, int r) 94 { 95 if (r<=a || b<=l) return INF; 96 if (a<=l && r<=b) return dat[k]; 97 else 98 { 99 int m=(l+r)/2; 100 int vl=query(a, b, k*2+1, l, m); 101 int vr=query(a, b, k*2+2, m, r); 102 return min(vl, vr); 103 } 104 }
