What does the 树状数组 do?
树状数组(Binary Indexed Tree(B.I.T), Fenwick Tree)是一个查询和修改复杂度都为log(n)的数据结构
主要用于查询任意两位之间的所有元素之和,但是每次只能修改一个元素的值
经过简单修改可以在log(n)的复杂度下进行范围修改
但是这时只能查询其中一个元素的值(如果加入多个辅助数组则可以实现区间修改与区间查询)
害,总的来说就是能 单点更新 区间查询 求区间最大值 区间修改+单点查询 区间修改+区间查询 单点修改+区间查询
是不是看起来很眼熟,是的,跟线段树的功能很类似,两者在复杂度上同级,但树状数组的常数却优于线段树,也比较好写,(不要被他的优势蒙蔽了双眼)他也有弊端,那就是实用性并没有线段树广,树状数组能解决的问题线段树都能解决,但反过来就不一定了,所以线段树也是要熟练掌握的(区间查询 / 修改这个特性使得线段树能够和树链剖分或者其他数据结构联动,从而达到解题的目的)
下面的内容参考自 https://bestsort.cn/2019/04/26/195/ 如果没看明白我说的,可以去大佬的博客看看QAQ
树状数组基础
很显然,这是一个二叉树

那么树状数组长什么样呢??

好像还不是很清楚?? 那这样子呢?

A[1],A[2],A[3]……表示原数组的权值,C数组,是求和之后的数组,C[i]就表示他的子树的叶子节点的权值和
好像没有什么特殊之处,让我们把他转换成二进制来看看
C[1] = C[0001] = A[1]; C[2] = C[0010] = A[1]+A[2]; C[3] = C[0011] = A[3]; C[4] = C[0100] = A[1]+A[2]+A[3]+A[4]; C[5] = C[0101] = A[5]; C[6] = C[0110] = A[5]+A[6]; C[7] = C[0111] = A[7]; C[8] = C[1000] = A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8];
你找到了什么规律,没找到那就再看看
跟从低位往高位数,连续的0的长度有关!我们设这个长度为k,例如 i=8(1000) 时,k=3;
那么这个节点管辖的区间为2^k(其中k为 i 二进制末尾0的个数)个元素
C[i]=A[i-2^k+1]+A[i-2^k+2]+……+A[i];
C[8]=A[8-2^3+1]+A[8-2^3+2]+……+A[8];
我们把这个图变成二进制

那么我们知道了k,又或者是知道了2^k,岂不是就可以进行更新和查询了
没错,下面介绍一个神奇的东西,可以在O(1)时间计算出2^k 不知道是哪位神犇大佬发明的 orz
int lowbit(int x) { return x&-x;}
对于一个数的负数就等于对这个数取反 +1 ,两者相与便是最低位的 1
其实很好理解,补码和原码必然相反,所以原码有 0 的部位补码全是 1 ,补码再 +1 之后由于进位那么最末尾的 1 和原码 最右边的 1 一定是同一个位置(当遇到第一个 1 的时候补码此位为 0 ,由于前面会进一位,所以此位会变为 1 ) 所以我们只需要进行a&(-a)就可以取出最低位的 1 了
例如: lowbit(22)=2
22的二进制原码011010 ,正数的补码等于它的原码011010
-22的二进制原码111010 ,负数的补码等于它的原码取反加1 ,为100110
011010 & 100110 = 000010正数转换成原码后是000010
所以lowbit(22)=2=2^1
在用的时候我们可以直接 #define lowbit(a) ((a)&-(a))
会了lowbit,我们就可以进行区间查询和单点更新啦
单点更新
时间复杂度
O(logn)
意义
update(x,y,n) => Ax=Ax+y
继续看开始给出的图 此时如果我们要更改A[1] 那么你要把A[1] A[2] A[4] A[8]全都改掉
1(001) C[1]+=A[1] lowbit(1)=001 1+lowbit(1)=2(010) C[2]+=A[1] lowbit(2)=010 2+lowbit(2)=4(100) C[4]+=A[1] lowbit(4)=100 4+lowbit(4)=8(1000) C[8]+=A[1]
代码:
void update(int x,int y,int n) { for(int i=x; i<=n; i+=lowbit(i)) ///x为更新的位置,y为更新后的数,n为数组大小 c[i] += y; }
区间查询
时间复杂度
O(logn)
意义
get_sum(x) => A1+A2+……+Ax
代码:
int get_sum(int x) { int ans = 0; for(int i=x; i; i-=lowbit(i)) ans += c[i]; return ans; }
求逆序对
原理可以去看这位大佬的博客:https://blog.csdn.net/SSimpLe_Y/article/details/53744096
懂了原理再让我们看看怎么做离散
离散化是程序设计中一个常用的技巧,它可以有效的降低时间复杂度。
有些数据本身很大,自身无法作为数组的下标保存对应的属性。如果这时只是需要这堆数据的相对属性,那么可以对其进行离散化处理。当数据只与它们之间的相对大小有关,而与具体是多少无关时,可以进行离散化。比如当你数据个数n很小,数据范围却很大时(超过1e9)就考虑离散化更小的值,能够实现更多的算法。
数组法:
for(int i=1;i<=n;i++) { cin>>a[i].val; a[i].id = i; } sort(a+1,a+n+1,cmp);//定义结构体时按val从小到大重载 for(int i=1;i<=n;i++) b[a[i].id]=i;//将a[i]数组映射成更小的值,b[i]就是a[i]对应的rank(顺序)值
二分法 (当然不用stl自己写一个也是极好的)
//n原数组大小 num原数组中的元素 lsh离散化的数组 cnt离散化后的数组大小 int lsh[MAXN],cnt,num[MAXN],n; for(int i=1;i<=n;i++) { scanf("%d",&num[i]); lsh[i]=num[i];//复制一份原数组 } sort(lsh+1,lsh+n+1);//排序,unique虽有排序功能,但交叉数据排序不支持,所以先排序防止交叉数据 //cnt就是排序去重之后的长度 cnt=unique(lsh+1,lsh+n+1)-lsh-1;//unique返回去重之后最后一位后一位地址-数组首地址-1 for(int i=1;i<=n;i++) num[i]=lower_bound(lsh+1,lsh+cnt+1,num[i])-lsh; //lower_bound返回二分查找在去重排序数组中第一个等于或大于num[i]的值的地址-数组首地址,从而实现离散化
下面是求逆序对的代码 对于数组 a,我们将其离散化处理为数组 b
单点更新和区间更新跟上面都是一样的
res的值就是逆序对数,别忘了初始化,b[i]应该大于0,如果你离散出来的时候b[i]=0 更新和查询时可以传入b[i]+1
void update(int x,int y,int n) { for(int i=x; i<=n; i+=lowbit(i)) c[i] += y; } int get_sum(int x) { int ans = 0; for(int i=x; i; i-=lowbit(i)) ans += c[i]; return ans; } for(int i=1; i<=n; i++) { update(b[i],1,n); res += i-get_sum(b[i]); }
求区间最大值
void update(int x,int y,int n) { for(int i=x; i<=n; i+=lowbit(i)) c[i] = max(c[i],y); } int query(int i) { int ans = 0; while(i) { ans = max(ans,c[i]); i-=lowbit(i); } return ans; }
区间修改+单点查询
通过“差分”来简化问题
什么?不知道什么是差分?前缀和晓得不,只不过记录的不是和,是差(记录数组中每个元素与前一个元素的差)
查询:
设原数组为a[i], 设数组d[i]=a[i]-a[i-1](a[0]=0),则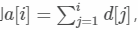 ,可以通过
,可以通过d[i]求的前缀和查询。
修改:
当给区间[l,r]加上x的时候,a[l]与前一个元素 a[l-1] 的差增加了x,a[r+1]与 a[r]的差减少了x。根据d[i]数组的定义,只需给a[l]加上 x, 给a[r+1] 减去x即可
代码:
void add(int p, int x) { while(p<=n) sum[p]+=x, p+=lowbit(p); } void range_add(int l, int r, int x) //给区间[l, r]加上x { add(l,x),add(r+1,-x); } int ask(int p) //单点查询 { int res = 0; while(p) res += sum[p], p-=lowbit(p); return res; }
区间修改+区间查询
基于上一个问题的“差分”思路,考虑一下如何在上一个问题构建的树状数组中求前缀和: 位置p的前缀和
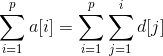
在等式最右侧的式子sum{i=1}^{p}sum{j=1}^{i}d[j]中,d[1]被用了p次,d[2]被用了p-1次……那么我们可以写出: 位置p的前缀和
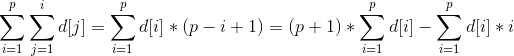
那么我们可以维护两个数组的前缀和: sum1[i]=d[i] sum2[i]=d[i]*i
查询:
位置p的前缀和即:(p+1)∗sum1数组中p的前缀和 - sum2数组中p的前缀和。 区间[l, r]的和即:位置r的前缀和 - 位置l的前缀和
修改:
对于sum1数组的修改同问题2中对d数组的修改。 对于sum2数组的修改也类似,我们给 sum2[l] 加上 l x,给 sum2[r + 1] 减去 (r + 1) x
代码:
void add(int p,int x) { for(int i=p;i<=n;i+=lowbit(i)) sum1[i]+=x,sum2[i]+=x*p; } void range_add(int l,int r,int x) { add(l,x), add(r+1,-x); } int ask(int p) { int res = 0; for(int i=p;i;i-=lowbit(i)) res += (p + 1) * sum1[i] - sum2[i]; return res; } int range_ask(int l,int r) { return ask(r)-ask(l-1); }
如果你感觉很乱的话 我整理了一下QAQ 下面是正经的,树状数组的板子
#define ll long long #define lowbit(a) ((a)&-(a)) void update(int x,ll y,int n)///One point update { for(int i=x; i<=n; i+=lowbit(i)) c[i] += y; } ll get_sum(int x)///Interval query { ll ans = 0; for(int i=x; i; i-=lowbit(i)) ans += c[i]; return ans; } void range_update(int l, int r, ll x) ///Add x to the interval [l, r] { update(l,x,n),update(r+1,-x,n); } ///区间更新+查询 for(int i=1; i<=n; i++)///初始化 { scanf("%lld",&a[i]); add(i,a[i]-a[i-1],n); } void add(int p,ll x,int n) ///Update interval { for(int i=p; i<=n; i+=lowbit(i)) sum1[i]+=x,sum2[i]+=x*p; } void range_add(int l,int r,ll x,int n) ///Add x to the interval [l, r] { add(l,x,n), add(r+1,-x,n); } ll ask(ll p) ///Interval ask2 { ll res = 0; for(int i=p; i; i-=lowbit(i)) res+=(p + 1)*sum1[i]-sum2[i]; return res; } ll range_ask(int l,int r) ///Interval ask1 { return ask(r)-ask(l-1); }
//至于二维树状数组这个坑,还是留着以后再填吧,散会