【学习笔记】树论—点分树(动态点分治)
【前言】
氡态淀粉质 / 垫粪鼠
点分治是一种树上分治算法,常用以处理树上路径相关信息的统计。在点分治的基础上加以变化,构造一颗支持快速修改的重构树,就成了点分树。
虽说名字里带个动态,但也有人认为它应该算作静态数据结构。
(据教练所说,点分树是近几年的新兴热门考点...于是就有了这篇总结...)
一:【算法理解及复杂度分析】
前置芝士:需要有良好的 点分治 基础。
点分治的核心思想在于依据重心划分子连通块,其良好的性质保证了最多只会分治 (log n) 层。有了这一特性,便可使用各种暴力计算答案。
那么我们按照分治递归的顺序提一颗新树出来,易知树高是 (O(log n)) 的。
具体地说,对于每一个找到的重心,将上一层分治时的重心设为它的父亲,得到一颗大小不变、最多 (log n) 层的虚树(或者理解为重构树。亦可称点分树,意义一样)。
在这颗虚树上,奇妙的性质产生了:虚树上所有点的子树大小之和为 (O(nlog n)) 。
证明很简单:每个点会被从根到它的路径上最多 (log n) 个祖先所统计,因此总复杂度为 (sum_{i=1}^{n}depth(i)=O(nlog n)) 。
如果要对某个点进行修改操作,直接在虚树上暴力跳父亲,改变 (O(log n)) 个祖先的虚子树信息即可。
Q: 虚子树的信息与原树有啥关系呢?
A: 点 (x) 在虚树上的子树集合就是原树中以 (x) 为重心(分治中心)时所囊括到的连通块。
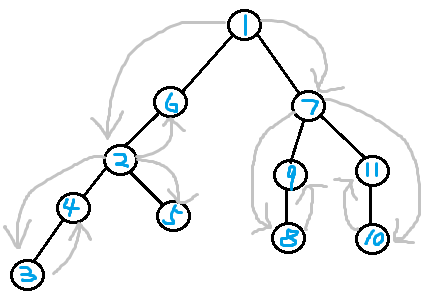
如下图(黑边为原树,灰边为虚树,蓝色编号为分治的顺序):
以 (1) 为重心做分治时,所囊括的连通块为 ({1,2,3,4,5,6,7,8,9,10}),删去该点后被划分为了 ({2,3,4,5,6},{7,8,9,10,11}) 两个子连通块;
以 (2) 为重心做分治时,所囊括的连通块为 ({2,3,4,5,6}),删去该点后被划分为了 ({3,4},{5},{6}) 三个子连通块;
以 (7) 为重心做分治时,所囊括的连通块为 ({7,8,9,10,11}),删去该点后被划分为了 ({8,9},{10,11}) 两个子连通块;
......
那么能用它求什么呢?
比如我们要统计某个点 (x) 到其他所有点的距离之和,即 (sum_{y=1}^{n}dis(x,y)) 。对于任意一个 (y),首先在虚树上找到它与 (x) 的 (lca)(或者说囊括连通块同时包含 (x,y) 的所有虚树节点中深度最深的那一个),易知在以此点为重心划分子连通块时 (x,y) 会首次被分割开来,因此该点必定在原树的 (x,y) 路径上。
所以我们只需要在这些 (lca) 的虚子树中寻找 (y) 即可,此时记录虚子树信息的作用便显现出来了。
而对于一个 (x),可能的 (lca) 最多存在 (log n) 个,因此通常使用暴力枚举+简单容斥的方法来统计 (y) 的贡献。具体见下文 【 计算贡献】。
二:【算法实现】
【模板】点分树 / 震波 ( ext{[P6329]}) ( ext{[Bzoj3730]})
【题目大意】 维护一颗带点权树,需要支持两种操作:修改 (x) 的点权,查询与点 (x) 距离不超过 (K) 的点权值之和。
1.【建点分树】
找到第一个重心 (rt) 后,先遍历整颗树得到 (rt) 的子树信息,然后删去 (rt),得到若干个连通块((rt) 的不同子树)。分别找到这些子树里的重心(在虚树上使其成为 (rt) 的儿子),然后递归处理这些子连通块。
实际上大体和淀粉质是相同的,只是将淀粉质中“计算答案”的操作改为了“统计虚子树信息”。
2.【计算贡献】
以下用 (fa_i) 表示点 (i) 在虚树上的父亲,(subtree(i)) 为点 (i) 在虚树上的子树集合,(fatree(i)) 为点 (i) 在虚树上的祖先集合,(dis(i,j)) 为 (i,j) 两点在原树上的距离,(A_i) 为点 (i) 的点权。
设:
(f_1(i,j)=sum_{xin subtree(i),dis(x,i)leqslant j}A_x),即虚树上 (i) 的子树中与 (i) 距离小于等于 (j) 的点权值之和;
为了除去某一个虚儿子子树的贡献,还需要:
(f_2(i,j)=sum_{xin subtree(i),dis(x,fa_i)leqslant j}A_x),即虚树上 (i) 的子树中与 (fa_i) 距离小于等于 (j) 的点权值之和。
在一次查询 ((x,k)) 中,对于虚树上的一对父子节点 ((i,fa_i)),(subtree(fa_i)-subtree(i)) 对答案的贡献为 (G(i,fa_i)=f_1(fa_i,k-dis(x,fa_i))) (-) (f_2(i,k-dis(x,fa_i))) 。
则有 (ans(x,k)=f_1(x,k)+) (sum_{iin fatree(x),fa_i eq 0} G(i,fa_i)),注意前面那个 (f_1(x,k)) 是因为容斥求和后 (subtree(x)) 没有被统计进去,所以要单独拿出来算。
修改点权时同理,把所有对于 (f_1,f_2) 的查询操作换成修改就可以了。
3.【维护信息】
计算 (dis) 可以用树剖求 ( ext{LCA}) 在线查询。
也可以用欧拉序 + ( ext{ST}) 表。或者用在每次找完根后,(dfs) 遍历一下子树预处理 (dis) 数组。两者都是花费 (O(nlog n)) 的时间省下了 (O(qlog^2 n)) 的时间,但经实际测试,( ext{ST}) 表被树剖吊起来锤,预处理与树剖不相上下,emm...过于柯怕
维护 (f_1,f_2) 可以对每个节点开一棵动态开点线段树,下标为 (dis)(即 (f_1,f_2) 的第二维)。时间复杂度为 (O(nlog^2 n)),空间按照 (dis) 范围的上界压缩一下可以做到 (O(nlog n))(如果偷懒统一使用同一个上界 ([0,n]) 可能会达到 (O(nlog^2 n)))。但线段树常数略大,可能会被卡(虽然我过了),换成树状数组会稳一点。
Q: 树状数组咋动态开点啊?
A: 当然是用动态分配内存的 (vector) 啊!
4.【实现细节】
-
子连通块大小不要直接用 ( ext{size(to)})(这都是从淀粉质那里遗留下来的问题了,但依旧有人不重视)
-
一般不需要把虚树的实际形态建出来,但如果能用到的话,注意不要和原树搞混。
-
树状数组大小要设置得当。设 (now=|subtree(i)|),由于 (i) 在 (subtree(i)) 中为重心,所以 (f_1(i,j)) 中 (j) 的值域为 ([0sim frac{now}{2}]),(f_2(i,j)) 中 (j) 的值域为 ([1sim now]) 。由于下标可以为 (0),在树状数组内部还需要统一向后移一位。也就是说 (f_1,f_2) 的大小要分别设置为 (frac{now}{2}+1) 和 (now+1) 。
-
如果预处理了每个点在虚树上的祖先,修改 / 查询 中跳父亲时需要倒序枚举(具体见代码)。
-
关于卡常:点分树做题经常会用到 ( ext{vector},) ( ext{set},) ( ext{multiset},) ( ext{priority queue}) 之类的东西,如果您嫌弃它们太慢且不愿开 ( ext{O2}),自备几个能代替 ( ext{STL}) 的模板吧....
5.【Code】
(线段树的代码就不放了)
【在线查询 Dis】
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<vector>
#define LL long long
#define Re register int
using namespace std;
const int N=1e5+3,inf=2e9,logN=17;
int n,m,o,x,y,T,op,lastans,A[N],deep[N],head[N];
struct QAQ{int to,next;}a[N<<1];
inline void add(Re x,Re y){a[++o].to=y,a[o].next=head[x],head[x]=o;}
inline void in(Re &x){
int f=0;x=0;char c=getchar();
while(c<'0'||c>'9')f|=c=='-',c=getchar();
while(c>='0'&&c<='9')x=(x<<1)+(x<<3)+(c^48),c=getchar();
x=f?-x:x;
}
struct LCA{
int fa[N],top[N],son[N],size[N];
inline void dfs1(Re x,Re Fa){
size[x]=1,deep[x]=deep[fa[x]=Fa]+1;
for(Re i=head[x],to;i;i=a[i].next)
if((to=a[i].to)!=Fa){
dfs1(to,x),size[x]+=size[to];
if(size[son[x]]<size[to])son[x]=to;
}
}
inline void dfs2(Re x,Re rt){
top[x]=rt;
if(!son[x])return;
dfs2(son[x],rt);
for(Re i=head[x],to;i;i=a[i].next)
if((to=a[i].to)!=fa[x]&&to!=son[x])dfs2(to,to);
}
inline void build(){dfs1(1,0),dfs2(1,1);}
inline int lca(Re x,Re y){
while(top[x]!=top[y]){
if(deep[top[x]]<deep[top[y]])swap(x,y);
x=fa[top[x]];
}
if(deep[x]>deep[y])swap(x,y);
return x;
}
}T1;
inline int Dis(Re x,Re y){return deep[x]+deep[y]-(deep[T1.lca(x,y)]<<1);}//查询原树中点x,y的距离
struct BIT{
int n;vector<int>C;
inline void build(Re N){C.resize((n=N)+1);}//使用到的上限为n,空间开n+1
inline void add(Re x,Re v){++x;while(x<=n)C[x]+=v,x+=x&-x;}//由于dis可能为0,所以在BIT里面统计向后移一位,查询同理
inline int ask(Re x){++x,x=min(x,n);Re ans=0;while(x)ans+=C[x],x-=x&-x;return ans;}//注意要和维护的上界取最小值,防止越界
}TR1[N],TR2[N];
int rt,sum,fa[N],vis[N],maxp[N],size[N];
inline void getrt(Re x,Re fa){//获取该连通块的重心
size[x]=1,maxp[x]=0;
for(Re i=head[x],to;i;i=a[i].next)
if(!vis[to=a[i].to]&&to!=fa)
getrt(to,x),size[x]+=size[to],maxp[x]=max(maxp[x],size[to]);
maxp[x]=max(maxp[x],sum-size[x]);
if(maxp[x]<maxp[rt])rt=x;
}
inline void sakura(Re x,Re Fa){//处理重心x所囊括的连通块
Re now=sum;vis[x]=1,fa[x]=Fa;
TR1[x].build(now/2+1),TR2[x].build(now+1);//由重心性质可知,TR1会使用[0,now/2],TR2会使用[1,now],向后移一位变为[1,now/2+1]和[2,now+1]
for(Re i=head[x],to;i;i=a[i].next)
if(!vis[to=a[i].to])
sum=size[to]>size[x]?now-size[x]:size[to],maxp[rt=0]=inf,getrt(to,0),sakura(rt,x);//注意子连通块大小不要直接用size[to]
}
inline void change(Re x,Re v){
TR1[x].add(0,v);//subtree(x)
for(Re i=x;fa[i];i=fa[i]){//在虚树上面跳父亲
Re tmp=Dis(x,fa[i]);
TR1[fa[i]].add(tmp,v);
TR2[i].add(tmp,v);
}
}
inline int ask(Re x,Re K){
Re ans=TR1[x].ask(K);//subtree(x)
for(Re i=x;fa[i];i=fa[i]){//在虚树上面跳父亲
Re tmp=Dis(x,fa[i]);if(tmp>K)continue;
ans+=TR1[fa[i]].ask(K-tmp);
ans-=TR2[i].ask(K-tmp);
}
return ans;
}
int main(){
// freopen("123.txt","r",stdin);
in(n),in(T),m=n-1;
for(Re i=1;i<=n;++i)in(A[i]);
while(m--)in(x),in(y),add(x,y),add(y,x);
T1.build(),sum=n,maxp[rt=0]=inf,getrt(1,0),sakura(rt,0);
for(Re i=1;i<=n;++i)change(i,A[i]);
while(T--){
in(op),in(x),in(y),x^=lastans,y^=lastans;
if(op)change(x,y-A[x]),A[x]=y;
else printf("%d
",lastans=ask(x,y));
}
}
【预处理 Dis】
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<vector>
#define LL long long
#define Re register int
using namespace std;
const int N=1e5+3,inf=2e9,logN=17;
int n,m,o,x,y,T,op,lastans,A[N],head[N];
struct QAQ{int to,next;}a[N<<1];
inline void add(Re x,Re y){a[++o].to=y,a[o].next=head[x],head[x]=o;}
inline void in(Re &x){
int f=0;x=0;char c=getchar();
while(c<'0'||c>'9')f|=c=='-',c=getchar();
while(c>='0'&&c<='9')x=(x<<1)+(x<<3)+(c^48),c=getchar();
x=f?-x:x;
}
struct BIT{
int n;vector<int>C;
inline void build(Re N){C.resize((n=N)+1);}//使用到的上限为n,空间开n+1
inline void add(Re x,Re v){++x;while(x<=n)C[x]+=v,x+=x&-x;}//由于dis可能为0,所以在BIT里面统计向后移一位,查询同理
inline int ask(Re x){++x,x=min(x,n);Re ans=0;while(x)ans+=C[x],x-=x&-x;return ans;}//注意要和维护的上界取最小值,防止越界
}TR1[N],TR2[N];
int rt,sum,gs[N],vis[N],maxp[N],size[N],frt[N][20],fdis[N][20];
inline void getrt(Re x,Re fa){//获取该连通块的重心
size[x]=1,maxp[x]=0;
for(Re i=head[x],to;i;i=a[i].next)
if(!vis[to=a[i].to]&&to!=fa)
getrt(to,x),size[x]+=size[to],maxp[x]=max(maxp[x],size[to]);
maxp[x]=max(maxp[x],sum-size[x]);
if(maxp[x]<maxp[rt])rt=x;
}
inline void getdis(Re x,Re rt,Re fa,Re d){//遍历该连通块预处理dis
frt[x][++gs[x]]=rt,fdis[x][gs[x]]=d;//顺手把祖先也存下来,后面一起访问
for(Re i=head[x],to;i;i=a[i].next)
if(!vis[to=a[i].to]&&to!=fa)getdis(to,rt,x,d+1);
}
inline void sakura(Re x){//处理重心x所囊括的连通块
Re now=sum;vis[x]=1,getdis(x,x,0,0);
TR1[x].build(now/2+1),TR2[x].build(now+1);//由重心性质可知,TR1会使用[0,now/2],TR2会使用[1,now],向后移一位变为[1,now/2+1]和[2,now+1]
for(Re i=head[x],to;i;i=a[i].next)
if(!vis[to=a[i].to])
sum=size[to]>size[x]?now-size[x]:size[to],maxp[rt=0]=inf,getrt(to,0),sakura(rt);//注意子连通块大小不要直接用size[to]
}
inline void change(Re x,Re v){
TR1[x].add(0,v);//subtree(x)
for(Re i=gs[x];i>=2;--i){//注意要倒序枚举
Re tmp=fdis[x][i-1];
TR1[frt[x][i-1]].add(tmp,v);
TR2[frt[x][i]].add(tmp,v);
}
}
inline int ask(Re x,Re K){
Re ans=TR1[x].ask(K);//subtree(x)
for(Re i=gs[x];i>=2;--i){//注意要倒序枚举
Re tmp=fdis[x][i-1];if(tmp>K)continue;
ans+=TR1[frt[x][i-1]].ask(K-tmp);
ans-=TR2[frt[x][i]].ask(K-tmp);
}
return ans;
}
int main(){
// freopen("123.txt","r",stdin);
in(n),in(T),m=n-1;
for(Re i=1;i<=n;++i)in(A[i]);
while(m--)in(x),in(y),add(x,y),add(y,x);
sum=n,maxp[rt=0]=inf,getrt(1,0),sakura(rt);
for(Re i=1;i<=n;++i)change(i,A[i]);
while(T--){
in(op),in(x),in(y),x^=lastans,y^=lastans;
if(op)change(x,y-A[x]),A[x]=y;
else printf("%d
",lastans=ask(x,y));
}
}
三:【常见套路、经典例题】
(注: 后面的题都不再用文字具体阐述 (f_1,f_2) 含义,且只放核心代码)
1.【另外两道板题】
-
烁烁的游戏 ( ext{[Bzoj4372]}) (和模板题震波类似,用一个数据结构进行维护)
-
( ext{Atm}) 的树 ( ext{[Bzoj4317] [Bzoj2051] [Bzoj2117]})(二分答案后又是一只震波)
2.【开店】
【题目大意】 维护一颗带点权、边权树,每次给出 (x,l,r),查询 (sum_{lleqslant A_y leqslant r}dis(x,y)),其中 (A_y) 为 (y) 的点权。
说起这道题,想起一张图(来自 ( ext{hychyc}) 巨佬的主席树做法)

(窝还是老老实实打点分树吧...)

(1).【分析】
统计贡献还是和模板题一样的套路,设:
(f_1(i,j)=sum_{xin subtree(i),A_xleqslant j}dis(x,i))
(f_2(i,j)=sum_{xin subtree(i),A_xleqslant j}dis(x,fa_i))
在查询点 (x) 的答案时,上面只算了合法点到祖先的距离,漏掉了 (x) 到 (fa_i) 这一段,所以还要记点数:
(g_1(i,j)=sum_{xin subtree(i),A_xleqslant j}1)(这里就不需要设 (g_2) 了,直接相减即可)。
查询时差分一下,只算权值小于等于 (k) 的距离之和。
则有 (ans(x,k)=f_1(x,k)+) (sum_{iin fatree(x),fa_i eq 0} G(i,fa_i))
其中 (G(i,fa_i)=) (f_1(fa_i,k)-f_2(i,k)) (+dis(x,fa_i) imes (g_1(fa_i,k)-g_1(i,k))) 。
由于这题没有修改操作,所以直接在建虚树时开个 ( ext{vector}) 预排序,顺便求出前缀和,查询时二分位置即可。
另外,为减小常数可以把柿子拆开,在一次 (k) 查询中对于虚树上每个祖先只使用一次二分。
空间复杂度:(O(nlog n)) 。
时间复杂度:(O((n+q)log^2 n)) 。
(2).【Code】
struct QWQ{
int v;LL S1,S2;QWQ(Re V=0,LL s1=0,LL s2=0){v=V,S1=s1,S2=s2;}
inline bool operator<(const QWQ &O)const{return v<O.v;}
};
vector<QWQ>TR[N];
inline void getdis(Re x,Re fa,Re rt,Re d){
TR[rt].push_back(QWQ(A[x],d,Fa[rt]?Dis(x,Fa[rt]):0));//如果rt没有父亲就不要求dis了
for(Re i=head[x],to;i;i=a[i].next)if(!vis[to=a[i].to]&&to!=fa)getdis(to,x,rt,d+a[i].w);
}
inline void sakura(Re x){
Re now=sum;vis[x]=1,getdis(x,0,x,0);
sort(TR[x].begin(),TR[x].end());//预排序
for(Re i=1;i<now;++i)TR[x][i].S1+=TR[x][i-1].S1,TR[x][i].S2+=TR[x][i-1].S2;//前缀和
for(Re i=head[x],to;i;i=a[i].next)if(!vis[to=a[i].to])
sum=size[to]>size[x]?now-size[x]:size[to],maxp[rt=0]=inf,getrt(to,0),Fa[rt]=x,sakura(rt);
}
inline QWQ get(Re x,Re K){//获取权值小于等于K的点信息之和
vector<QWQ>::iterator it=upper_bound(TR[x].begin(),TR[x].end(),QWQ(K));
if(it==TR[x].begin())return QWQ();--it;return QWQ((it-TR[x].begin())+1,it->S1,it->S2);
}
inline LL ask(Re x,Re K){//查询权值小于等于K的点与x的距离之和
QWQ TR=get(x,K);LL ans=TR.S1;
if(Fa[x])ans-=TR.S2+(LL)Dis(x,Fa[x])*TR.v;//为迎合拆柿子,这里把第一次计算拿出来了
for(Re i=Fa[x];i;i=Fa[i]){
TR=get(i,K),ans+=TR.S1+(LL)Dis(x,i)*TR.v;
if(Fa[i])ans-=TR.S2+(LL)Dis(x,Fa[i])*TR.v;
}
return ans;
}
3.【幻想乡战略游戏】
幻想乡战略游戏 ( ext{[ZJOI2015] [P3345]})
【题目大意】 维护一颗带点权、边权树(树上点的度数不超过 (20))。现有若干次修改点权的操作,每次操作结束后您需要选出一个核心点 (x) 使得 (F(x)) 最小,其中 (F(x)=sum_{i=1}^{n}dis(x,i) imes A_i),(A_i) 为 (i) 的点权。
(1).【分析】
这题关键在于分析性质猜结论。
假设当前核心为 (x),将 (x) 设为树的根,定义 (S_A(i)) 为 (i) 子树内所有点的点权之和。
对于 (x) 的任意一个儿子节点 (y),若将核心改为 (y),那么 (Delta F_{x o y} =F(y)-F(x)=(S_A(x)-2S_A(y)) imes dis(x,y)) 。选 (y) 更优当且仅当满足 (Delta F_{x o y}<0) 即 (S_A(x)<2S_A(y)),易知对于一个 (x) 满足该式的 (y) 最多只存在一个。
于是一个经过优化的暴力就产生了:每次询问从根开始,不断进入比它更优的儿子,如果找不到更优则说明本身已是最优。
但很多人只讲到这些就开始扯点分树信息维护了,实际上是不严谨的,我们还需要证明:“在以 (x) 为根时,若 (y) 没有 (x) 优秀(表现为 (Delta F_{x o y}>0)),则 (y) 子树里的点也一定没有 (x) 优秀”。
设 (y) 的儿子为 (y'),考虑还是在以 (x) 为根的前提下记算贡献:
(Delta F_{y o y'}) (=(S_A(y)-2S_A(y')+S_A(x)-S_A(y)) imes dis(y,y')) (=(S_A(x)-2S_A(y')) imes dis(y,y'))
又因为 (S_A(y)geqslant S_A(y'))(这题 (A_i) 应该是不为负的,所以能得出这个关系式)
若 (Delta F_{x o y}>0) 则 (S_A(x)>2S_A(y)geqslant 2S_A(y'))
因此 (Delta F_{y o y'}>0,) (Delta F_{x o y'}=Delta F_{x o y}+Delta F_{y o y'}>0) 。
证毕。
暴力单次询问复杂度 (O(20depth)),而点分树有着 (depth=O(log n)) 的天然优势,我们可以把跳儿子的过程转移到点分树上进行。具体的说,从第一个重心开始,枚举它在原树上的儿子,若找到了比他更优的点,则跳到该子树(或者说子连通块)的重心。容易证明这样做一定不会错过最优解。
现在的问题只剩下快速计算 (F(x)) 了,按照套路,设:
(f_1(i)=sum_{xin subtree(i)}dis(x,i) imes A_x)
(f_2(i)=sum_{xin subtree(i)}dis(x,fa_i) imes A_x)
(g_1(i)=sum_{xin subtree(i)}A_x)
则有 (F(x)=f_1(x)+) (sum_{iin fatree(x),fa_i eq 0} G(i,fa_i))
其中 (G(i,fa_i)=) (f_1(fa_i)-f_2(i)) (+dis(x,fa_i) imes (g_1(fa_i)-g_1(i))) 。
由于这题的 (f_1,f_2,g_1) 都只有一维,直接用数组存下来就好了。
空间复杂度:(O(nlog n)) 。
时间复杂度:(O(nlog n+20qlog^2n)) 。
(这题不知为啥常数小得惊人,不吸氧最慢的点只跑了 (900ms))
(2).【Code】
inline void change(Re x,Re v){//Sv即为g1
TR1[x]+=v*0,Sv[x]+=v;
for(Re i=gs[x];i>=2;--i){
Re tmp=fdis[x][i-1];
TR1[frt[x][i-1]]+=(LL)v*tmp;
TR2[frt[x][i]]+=(LL)v*tmp;
Sv[frt[x][i-1]]+=v;
}
}
inline LL ask(Re x){//计算F(x)
LL ans=TR1[x];
for(Re i=gs[x];i>=2;--i){
Re tmp=fdis[x][i-1];
ans+=TR1[frt[x][i-1]];
ans-=TR2[frt[x][i]];
ans+=(LL)(Sv[frt[x][i-1]]-Sv[frt[x][i]])*tmp;
}
return ans;
}
inline LL find(Re x){
LL tmp=ask(x);
for(Re i=T0.head[x];i;i=T0.a[i].next)//这里枚举原树
if(ask(T0.a[i].to)<tmp)return find(T0.a[i].rt);//如果to比x优秀就进入to所在连通块的重心(x在虚树上的儿子)
return tmp;
}
4.【小清新数据结构题】
【题目大意】 维护一颗带点权树,需要支持两种操作:修改 (x) 的点权,查询以点 (x) 为根时的 (sum_{i=1}^{n}(sum_{jin sub(i)}A_j)^2),其中(A_j) 为 (j) 的点权,(sub(i)) 为点 (i) 子树内的节点集合。
(1).【分析】
一看就知道是个丧心病狂拆柿子题。
上公式(以 (x) 为根):
设 (sum=sum_{i=1}^{n}A_i),(S(i)=sum_{jin sub(i)}A_j)
(sum_{i=1}^{n}S_i) (=sum_{i=1}^{n}A_i(dis(i,x)+1)) (=sum+sum_{i=1}^{n}dis(i,x) imes A_i)(每个点会在自己以及它的 (dis) 个祖先处被统计到)
设 (F=sum_{i=1}^{n}dis(i,x) imes A_i)(用与 幻想乡战略游戏 同样的方法可以求得)
由于 (sum_{i=1}^{n}S_i(sum-S_i)) 始终为一个定值(对于每条边 (x,y),两边的连通块点权之和乘起来然后再求和),我们可以先 (O(n)) 预处理出来,设为 (tmp) 。
则 (ans(x)=sum_{i=1}^{n}S_i^2) (=sumsum_{i=1}^{n}S_i-tmp) (=sum(sum+F)-tmp) 。
空间复杂度:(O(nlog n)) 。
时间复杂度:(O((n+q)log n)) 。
(2).【Code】
代码就不放了,毕竟和上一道差不多,只是多了个 (dfs) 预处理 (tmp)。

5.【成都七中】
成都七中 ( ext{[Ynoi2011] [P5311]})
【题目大意】 由一颗树,树上每个节点有一种颜色,每次查询给出 (l,r,x),求保留树上编号在 ([l,r]) 内的点,(x) 所在联通块中颜色种类数。
(1).【分析】
这题比较难想。
先建出点分树,对于一次查询 ((l,r,x)),在点分树上 (x) 的祖先中找到深度最小的点 (pa),且满足 (x) 只经过编号 ([l,r]) 内的点在原树上能到达 (pa) 。记一下每个点 (i) 到虚树祖先的路径上所经过的节点编号最小/大值就可以轻松求得(分别记为 (d_{min}(i,j)) 和 (d_{max}(i,j)))。
分析可知:(x) 只经过编号 ([l,r]) 内的点所在的连通块被完全包含在了 (subtree(pa)) 中(虚子树)。我们把本次询问放到 (pa) 节点处,最后再统一离线处理。
枚举虚树上的点 (rt),处理该节点处的询问时,对于任意一个 ((l,r,x)),满足 (lleqslant d_{min}(i,rt)) 且 (d_{max}(i,rt)leqslant r) 的 (i) 即为与 (x) 在同一连通块内的点,现需要统计这些点的颜色种类。
显然是个偏序问题,把询问和节点信息放一起按 (l) 排序,指针从右往左扫,同时记录每种颜色节点右端点最小的位置,再开一棵树状数组维护每个位置上的数量,便可直接查询了。
空间复杂度:(O(nlog n)) 。
时间复杂度:(O(nlog^2 n)) 。
(2).【Code】
struct Query{int l,r,id,co;inline bool operator<(const Query &O)const{return l!=O.l?l>O.l:id<O.id;}};vector<Query>Q[N];
inline void getdis(Re x,Re rt,Re fa,Re d1,Re d2){//d1:最小值 d2:最大值
d1=min(d1,x),d2=max(d2,x),Q[rt].push_back((Query){d1,d2,0,A[x]});
frt[x][++gs[x]]=rt,fd1[x][gs[x]]=d1,fd2[x][gs[x]]=d2;
for(Re i=head[x],to;i;i=a[i].next)if(!vis[to=a[i].to]&&to!=fa)getdis(to,rt,x,d1,d2);
}
inline void change(Re x,Re l,Re r,Re id){//插入第id次询问l,r,x
for(Re i=1;i<=gs[x];++i)
if(l<=fd1[x][i]&&fd2[x][i]<=r){Q[frt[x][i]].push_back((Query){l,r,id,0});break;}
}
struct BIT{
int C[N];
inline void CL(Re x){while(x<=n)C[x]=0,x+=x&-x;}
inline void add(Re x,Re v){while(x<=n)C[x]+=v,x+=x&-x;}
inline int ask(Re x){Re ans=0;while(x)ans+=C[x],x-=x&-x;return ans;}
}TR;
inline int GetAns(){
for(Re i=1;i<=100000;++i)mir[i]=inf;
for(Re rt=1;rt<=n;++rt){//枚举点分树上的点
sort(Q[rt].begin(),Q[rt].end());
for(IT it=Q[rt].begin();it!=Q[rt].end();++it)
if(it->id)Ans[it->id]=TR.ask(it->r);//查询
else if(it->r<mir[it->co])TR.add(mir[it->co],-1),TR.add(mir[it->co]=it->r,1);//节点信息,更新此颜色的最小右端点
for(IT it=Q[rt].begin();it!=Q[rt].end();++it)
if(!(it->id))TR.CL(mir[it->co]),mir[it->co]=inf;
}
}
6.【Iqea】
【题目大意】 二维平面上给出若干个点的坐标,在这些点处打好地基(保证为一个四连通块,且不会出现封闭的空地)。有两种操作:在 ((x,y)) 处建造商店,询问离 ((x,y)) 最近的商店与 ((x,y)) 的距离大小。两点距离定义为只经过有地基的点的最短路径长度,相邻两个格子距离为 (1) 。保证每次给出的坐标处一定有地基。
(1).【分析】
一只神薙。
首先是非常巧妙的建图:每一行分开看,把同一行的若干个联通块分别缩成点,然后向四周相邻的点连边,由于没有封闭的空地,这样连出来一定是棵树。
支持加入关键点,查询距离最近的关键点,建点分树?
似乎还没做完:两点之间的最短距离要如何在树上表示呢?
看图:

任选 (a,b) 路径上一个缩成点的小连通块 (m) 作为中介(如图中黄色框),先分别求出 (a,b) 移动到中介的最短路径 (d_a(m),d_b(m)),并记录它们到达中介时的纵坐标 (y_a(m),y_b(m))(在图中表现为 (1) 号和 (8) 号位置),则 (dis(a,b)=d_a(m)+d_b(m)+|y_a(m)-y_b(m)|),即 (min{d_a(m)+d_b(m)+y_a(m)-y_b(m),d_a(m)+d_b(m)+y_b(m)-y_a(m)}) 。
现在点分树就可以轻松维护答案了,设:
(f_1(i,j)=sum_{xin subtree(i),y_x(i)leqslant j}d_x(i)-y_x(i))
(g_1(i,j)=sum_{xin subtree(i),y_x(i)geqslant j}d_x(i)+y_x(i))
则有 (ans(x,k)=) (min_{iin fatree(x)}) (min{d_x(i)+y_x(i)+f_1(i,y_x(i)),d_x(i)-y_x(i)+g_1(i,y_x(i))})
二维的 (f_1,g_1) 用树状数组维护。
空间复杂度:(O(nlog n)) 。
时间复杂度:(O(nlog n+qlog^2 n)) 。
(2).【Code】
int ip_O,n,o,x,y,T,op,MaxX,X[N],ip[N],Yl[N],Yr[N],idl[N],idr[N],head[N];vector<int>V[N];map<int,int>id[N];
struct QAQ{int to,next;}a[N<<1];//外层的这个是缩图所得到的树
inline void add(Re x,Re y){a[++o].to=y,a[o].next=head[x],head[x]=o;}
struct Tree{
int o,head[N];
struct QAQ{int to,next;}a[N<<2];
inline void add_(Re x,Re y){a[++o].to=y,a[o].next=head[x],head[x]=o;}
inline void add(Re x,Re y){add_(x,y),add_(y,x);}
}T0;//T0:以二维平面上的连通性建成的图
inline void get_tree(){//缩图建树
for(Re i=1;i<=n;++i)in(x),in(y),MaxX=max(MaxX,x),V[x].push_back(y),id[x][y]=i;
for(Re x=1;x<=MaxX;++x)if(!V[x].empty()){
sort(V[x].begin(),V[x].end());
Re last=-1;idl[x]=ip_O+1;
for(Re J=0,SZ=V[x].size(),y;J<SZ;last=V[x][J],++J){
if(last+1!=(y=V[x][J]))ip[id[x][y]]=++ip_O,X[ip_O]=x,Yl[ip_O]=Yr[ip_O]=y;
else ip[id[x][y]]=ip_O,Yr[ip_O]=y,T0.add(id[x][y],id[x][y-1]);
if(id[x-1].find(y)!=id[x-1].end())T0.add(id[x-1][y],id[x][y]);
}
idr[x]=ip_O;
if(V[x-1].empty())continue;
Re k=idl[x-1];
for(Re j=idl[x];j<=idr[x];++j){
while(k<=idr[x-1]&&Yr[k]<Yl[j])++k;
for(Re k_=k;k_<=idr[x-1]&&Yl[k_]<=Yr[j];++k_)add(k_,j),add(j,k_);
}
}
}
struct QWQ{
int d,y;QWQ(Re D=0,Re Y=0){d=D,y=Y;}
inline bool operator<(const QWQ &O)const{return d<O.d;}
};
struct BIT{
int n,op;vector<int>C;//op=0:前缀 op=1:后缀(把询问、查询里的x都翻转一下就是了)
inline void build(Re N){n=N,C.push_back(inf);while(N--)C.push_back(inf);}//这里就不用resize了,因为要初始化为inf
inline void add(Re x,Re v){if(op)x=n-x+1;while(x<=n)C[x]=min(C[x],v),x+=x&-x;}
inline int ask(Re x){if(op)x=n-x+1;Re ans=inf;while(x)ans=min(ans,C[x]),x-=x&-x;return ans;}
}TR1[N],TR2[N];
int rt,sum,gs[N],vis[N],maxp[N],size[N],frt[N][22];QWQ fdis[N][22];
inline void getrt(Re x,Re fa){
size[x]=Yr[x]-Yl[x]+1,maxp[x]=0;//注意size的初始化不是1
for(Re i=head[x],to;i;i=a[i].next)if(!vis[to=a[i].to]&&to!=fa)
getrt(to,x),size[x]+=size[to],maxp[x]=max(maxp[x],size[to]);
maxp[x]=max(maxp[x],sum-size[x]);if(maxp[x]<maxp[rt])rt=x;
}
int Q[N],pan[N];QWQ dis[N];
inline void getdis0(Re rt){//bfs
Re h=1,t=0;
for(Re i=Yl[rt];i<=Yr[rt];++i)pan[Q[++t]=id[X[rt]][i]]=rt,dis[Q[t]]=QWQ(0,i-Yl[rt]+1);
while(h<=t){
Re x=Q[h++];
for(Re i=T0.head[x],to;i;i=T0.a[i].next)
if(pan[to=T0.a[i].to]!=rt&&!vis[ip[to]])
dis[to]=QWQ(dis[x].d+1,dis[x].y),pan[Q[++t]=to]=rt;
}
}
inline void getdis(Re x,Re rt,Re fa){
frt[x][++gs[x]]=rt;
for(Re i=Yl[x];i<=Yr[x];++i)fdis[id[X[x]][i]][gs[x]]=dis[id[X[x]][i]];//距离在bfs中已获得
for(Re i=head[x],to;i;i=a[i].next)if(!vis[to=a[i].to]&&to!=fa)getdis(to,rt,x);
}
inline void sakura(Re x){
Re now=sum;vis[x]=1,getdis0(x),getdis(x,x,0);
TR1[x].build(Yr[x]-Yl[x]+1),TR2[x].build(Yr[x]-Yl[x]+1),TR2[x].op=1;//树状数组的使用范围为[1,Yr-Yl+1]
for(Re i=head[x],to;i;i=a[i].next)if(!vis[to=a[i].to])
sum=size[to]>size[x]?now-size[x]:size[to],maxp[rt=0]=inf,getrt(to,0),sakura(rt);
}
inline void change(Re y){
Re x=ip[y];
for(Re i=gs[x];i;--i)
TR1[frt[x][i]].add(fdis[y][i].y,fdis[y][i].d-fdis[y][i].y),
TR2[frt[x][i]].add(fdis[y][i].y,fdis[y][i].d+fdis[y][i].y);
}
inline int ask(Re y){
Re x=ip[y],ans=inf;
for(Re i=gs[x];i;--i)
ans=min(ans,fdis[y][i].d+fdis[y][i].y+TR1[frt[x][i]].ask(fdis[y][i].y)),
ans=min(ans,fdis[y][i].d-fdis[y][i].y+TR2[frt[x][i]].ask(fdis[y][i].y));
return ans;
}
7.【大毒瘤】
相信您已经积累了足够的实力,下面我们来看一道果题吧QAQ
紫荆花之恋 ( ext{[WC2014] [P3920]})
四:【总结】
模板及例题 (1.1,1.2) 都是靠数据结构维护贡献,例 (2) 则换成了 ( ext{STL}) 。套娃行为所导致的的码量增加以及大常数都是值得关注的问题。
例 (3,4) 主要是按照容斥套路推式子,相对比较好掌握,但细节较多,要注意统计贡献时补充不漏。
例 (5) 难点在于利用点分树的特殊性质转离线。点分树各种神奇的特性,对应到不同的题上就会有各种神奇的解法。如果没有强大的瞎蒙猜结论能力,就多刷刷题吧,见多识广总没有坏处的。
例 (6) 不光要会神仙建图,还要想办法用点分树能维护的东西来表示两点距离。这道题有效地提醒了我们:点分树有着不错的灵活性,并非只有那个一成不变的模板,所以不要死记硬背啊...
Q: 话说点分树能搞可持久化吗?
A: 虽然听起来比较毒瘤,但不瞒您说,还真可以(具体见 可持久化点分树)