一．预备知识
积性函数的内容在另外一篇随笔中。
二．重要知识
关于莫比乌斯反演，有很多很好的博客，这里推荐几个
莫比乌斯反演入门 对于这篇博客中的内容，只需要知道 (mu) 其实是一种容斥系数即可，具体的乱七八糟的过程无需理会
莫比乌斯反演简要笔记
（一）莫比乌斯函数
１．莫比乌斯函数 (mu(n)) 的性质
- 设 (n=p_{1}^{k_{1}}*p_{2}^{k_{2}}*...*p_{m}^{k_{m}})，其中 (p) 为素数，那么
[mu(n)=egin{cases}
1 quadquadquadquad n=1 \\
(-1)^{m} quad prod_{i=1}^{m}k_{i}=1 \\
0 quadquadquadquad otherwise
end{cases}]
-
莫比乌斯函数是积性函数，即(mu(a)mu(b)=mu(a cdot b))
-
(sum_{d|n} mu(d)=[n=1]) ,这一点根据二项式定理即可证明
２．线性筛莫比乌斯函数
需要用到的性质
根据 (mu) 的性质可以得到，如果 (n=p*m) ，其中 (p) 为 (n) 的质因子，如果 (p|m) 那么显然 (mu(n)=0) ，否则 (mu(n)=-mu(m))
miu[1]=1;
For (i,2,n) {
if (!vis[i]) {
p[++N]=i;
miu[i]=-1;
}
For (j,1,N) {
if (i*p[j]>n) break;
vis[i*p[j]]=1;
if (i%p[j]==0) {
miu[i*p[j]]=0;
break;
}
else
miu[i*p[j]]=-miu[i];
}
}
（二）莫比乌斯反演
如果 (f(n)) , (g(n)) 为数论函数，并且满足$$f(n)=sum_{d|n}g(d)$$
则有莫比乌斯反演$$g(n)=sum_{d|n}mu(d)*f(frac{n}{d})$$
证明在上面的博客中写得很清楚。
但是那个变形式的证明我一直没有弄得很明白，到底如何交换变量？
１．例题一
(bzoj2190)
求
[sum_{i=1}^{n}sum_{j=1}^{m}[gcd(i,j)=k]
]
[=sum_{i=1}^{leftlfloor frac{n}{k}
ight
floor}sum_{j=1}^{leftlfloor frac{m}{k}
ight
floor}[gcd(i,j)=1]
]
因为
[sum_{d|n}^{n}mu(d)=[n=1]
]
所以，可以化为
[=sum_{i=1}^{leftlfloor frac{n}{k}
ight
floor}sum_{j=1}^{leftlfloor frac{m}{k}
ight
floor}sum_{d|gcd(i,j)}mu(d)
]
改变枚举量，可以化为
[sum_{d=1}^{leftlfloorfrac{n}{k}
ight
floor} mu(d) leftlfloorfrac{n}{kd}
ight
floor leftlfloorfrac{m}{kd}
ight
floor
]
如果是暴力就是(O(n))的，可以用分块优化到(sqrt{n})
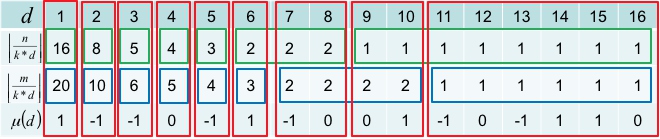
因为有很多取值是连续的，对于相等的段，我们求取(mu)的前缀和，即可批量计算这一个段的答案。
ll solve(int n,int m,int k) {
if (n>m) swap(n,m);
n/=k; m/=k;
ll ans=0;
for (int i=1,nxt=1;i<=n;i=nxt+1) {
nxt=min(n/(n/i),m/(m/i));
ans+=1ll*(sum[nxt]-sum[i-1])*(n/i)*(m/i);
}
return ans;
}
２．例题二
求
[sum_{i=1}^{n}sum_{j=1}^{m} gcd(i,j)^k
]
一个重要的方法枚举 (dx) 的乘积
[sum_{T=1}^{n} leftlfloorfrac{n}{T}
ight
floor leftlfloorfrac{m}{T}
ight
floor sum_{d|T}d^{k}mu(frac{T}{d})
]
然后设
[f(T)=sum_{d|T}d^{k}mu(frac{T}{d})
]
再根据积性函数的性质化简即可
具体的过程，上面博客里有，下面对其中的几点做一下说明
- 分块套分块的方法首先是分块(leftlfloor frac{n}{d} ight floor)，因为有很多是一样的，然后再分块 (mu) 后面的那两个
- 后面化简(f(n))的部分因为只有在 (d) 取到 (p_{i}^{x^{i}}) 或者 (p_{i}^{x^{i}-1}) 的时候 ((frac{T}{d})) 取到 (1) 或者 (p_{i}) 的时候 (mu) 值不为０。然后线筛积性函数。
注意，这道题目的解答过程对后面的题目很有帮助，一定要全部弄明白。
他推理的过程中有很多的变量都写错了，但是大体公式还是没问题的。
三．题目
（一）(bzoj2820)
求
[sum_{i=1}^{n}sum_{j=1}^{m}[gcd(i,j) isprime]
]
分析：
枚举质数
[=sum_psum_{i=1}^{leftlfloor frac{n}{p}
ight
floor}sum_{j=1}^{leftlfloor frac{m}{p}
ight
floor}[gcd(i,j)=1]
]
[=sum_{p}sum_{d=1}^{leftlfloor frac{n}{p}
ight
floor}mu(d)leftlfloor frac{n}{pd}
ight
floorleftlfloor frac{m}{pd}
ight
floor
]
然后枚举乘积(pd)
[=sum_{T=1}leftlfloor frac{n}{T}
ight
floor leftlfloor frac{n}{T}
ight
floorsum_{p|T}mu(frac{T}{p})
]
但是，如果设
[f(T)=sum_{p|T}mu(frac{T}{p})
]
(f(T))不是积性函数
所以需要用到一个新的方法，在预处理的时候，枚举质数 (p) ，枚举 (T) ，然后将 (p) 的每一个倍数 (T) 都加上 (mu(frac{T}{p})) ，然后求 (f(n)) 就可以做到 (O(1))
再加上前面的分块求 (T) ，因此总时间复杂度为 (O(Tsqrt{n}+maxn))
当然，还有一种方法，详情看here
最后再上代码
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
typedef long long ll;
typedef double dd;
#define For(i,j,k) for (int i=j;i<=k;++i)
#define Forr(i,j,k) for (int i=j;i>=k;--i)
#define Set(a,p) memset(a,p,sizeof(a))
using namespace std;
template<typename T>bool chkmax(T &a,T b) { return a<b?a=b,1:0; }
template<typename T>bool chkmin(T &a,T b) { return a>b?a=b,1:0; }
const int maxn=1e7+1e2;
const int maxx=1e7;
int n,m,N;
int p[maxn],miu[maxn],vis[maxn],sum[maxn],t[maxn];
inline void read(int &x) {
x=0;
int p=1;
char c=getchar();
while (!isdigit(c)) {if (c=='-') p=-1; c=getchar();}
while (isdigit(c)) {x=(x<<1)+(x<<3)+(c-'0'); c=getchar();}
x*=p;
}
inline void init() {
miu[1]=1;
For (i,2,maxx) {
if (!vis[i]) {
p[++N]=i; miu[i]=-1;
}
For (j,1,N) {
if (1ll*i*p[j]>maxx) break;
vis[i*p[j]]=1;
if (i%p[j]==0) {
miu[i*p[j]]=0;
break;
}
else miu[i*p[j]]=-miu[i];
}
}
For (i,1,N) {
for (int j=p[i];j<=maxx;j+=p[i]) t[j]+=miu[j/p[i]];
}
For (i,1,maxx) t[i]=t[i-1]+t[i];
}
int main() {
init();
int tt; read(tt);
while (tt--) {
read(n); read(m);
if (n>m) swap(n,m);
ll ans=0;
for (int i=1,nxt=1;i<=n;i=nxt+1) {
nxt=min(n/(n/i),m/(m/i));
ans+=1ll*(n/i)*(m/i)*(t[nxt]-t[i-1]);
}
printf("%lld
",ans);
}
return 0;
}
（二）(P3768)
求
[sum_{i=1}^{n}sum_{j=1}^{n}ijgcd(i,j)
]
[=sum_{d=1}^{n}dsum_{i=1}^{n}sum_{j=1}^{n}ij[gcd(i,j)=d]
]
[=sum_{d=1}^{n}d^3sum_{i=1}^{leftlfloor frac{n}{d}
ight
floor}sum_{j=1}^{leftlfloor frac{n}{d}
ight
floor}ij[gcd(i,j)=1]
]
[=sum_{d=1}^{n}d^3sum_{i=1}^{leftlfloor frac{n}{d}
ight
floor}sum_{j=1}^{leftlfloor frac{n}{d}
ight
floor}ijsum_{x|gcd(i,j)}mu(x)
]
[=sum_{d=1}^{n}d^3sum_{x=1}^{leftlfloor frac{n}{d}
ight
floor}mu(x)x^2sum_{i=1}^{leftlfloor frac{n}{dx}
ight
floor}sum_{j=1}^{leftlfloor frac{n}{dx}
ight
floor}ij
]
令(F(n)=sum_{i=1}^{n}sum_{j=1}^{n}ij=sum_{i=1}^{n}i^3=(sum_{i=1}^{n})^2)，所以
[=sum_{d=1}^{n}d^3sum_{x=1}^{leftlfloor frac{n}{d}
ight
floor}mu(x)x^2F(leftlfloor frac{n}{dx}
ight
floor)
]
令(T=dx)，改变枚举变量（干脆把向下取整去掉，反正程序中是这样的，不然写起来好麻烦）
[=sum_{T=1}^{n}sum_{d|T}d^3mu(frac{T}{d})(frac{T}{d})^2F(frac{n}{T})
]
[=sum_{T=1}^{n}F(frac{n}{T})T^2sum_{d|T}dmu(frac{T}{d})
]
然后，根据(mu)函数的性质，我们可以得到
[id*mu=1*varphi*mu=varepsilon*varphi=varphi
]
所以原式可化为
[=sum_{T=1}^{n}F(frac{n}{T})T^2varphi(T)
]
这看着就清爽多了！前半部分分块处理，后面杜教筛
设(f(i)=i^2*varphi(i))，(S(n)=sum_{i=1}^{n}f(i))
杜教筛公式：
[g(1)*S(n)=sum_{i=1}^{n}(f*g)(i)-sum_{i=2}^{n}g(i)*S(frac{n}{i})
]
设(g(x)=x^2)，那么
[(f*g)(i)=sum_{d|i}f(d)*g(frac{i}{d})=sum_{d|i}d^2*varphi(d)*(frac{i}{d})^2=i^2*sum_{d|i}varphi(d)=i^3
]
所以
[S(n)=sum_{i=1}^{n}i^3-sum_{i=2}^{n}i^2*S(frac{n}{i})
]
再然后，就可以开始打程序了！
当然，事实上是，用 (varphi) 更简单here
[=sum_{d=1}^{n}varphi(d)sum_{d|i}sum_{d|j}ij ][=sum_{d=1}^{n}varphi(d) d^2 sum_{i=1}^{leftlfloor frac{n}{d} ight floor}i^3 ]
我这篇代码被卡常了，对着别人的程序调了好久，但是还是很慢，不知道为什么......
在计算(sum)和(sq)是时候，(n)一进去就要取模！
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<map>
typedef double dd;
#define For(i,j,k) for (register ll i=j;i<=k;++i)
#define Forr(i,j,k) for (register ll i=j;i>=k;--i)
#define REP(i,j,k) for (register int i=j;i<=k;++i)
#define Set(a,p) memset(a,p,sizeof(a))
#define ll long long
using namespace std;
template<typename T>bool chkmax(T& a,T b) {return a<b?a=b,1:0;}
template<typename T>bool chkmin(T& a,T b) {return a>b?a=b,1:0;}
#define maxn 8000000+100
int maxx=8000000;
ll n,modd,Inv2,Inv6,ans;
int N,p[maxn];
ll phi[maxn];
bool vis[maxn];
map<ll,ll>Phi;
inline void init() {
phi[1]=1;
for (register int i=2;i<=maxx;++i) {
if (!vis[i]) {
p[++N]=i; phi[i]=i-1;
}
for (register int j=1;j<=N;++j) {
if (i*p[j]>maxx) break;
int k=i*p[j];
vis[k]=1;
if (i%p[j]==0) {
phi[k]=phi[i]*p[j]%modd;
break;
}
else phi[k]=phi[i]*(p[j]-1)%modd;
}
}
for (register int i=1;i<=maxx;++i) phi[i]=(phi[i-1]+phi[i]*i%modd*i%modd)%modd;
}
inline ll quick(ll a,ll b) {
ll s=1;
while (b) {
if (b&1) s=s*a%modd;
a=a*a%modd; b>>=1;
}
return s;
}
inline ll sum(ll n) {
n%=modd;
return n*(n+1)%modd*Inv2%modd;
}
inline ll sq(ll n) {
n%=modd;
return n*(n+1)%modd*(n+n+1)%modd*Inv6%modd;
}
ll calc(ll n) {
if (n<=N) return phi[n];
if (Phi[n]) return Phi[n];
ll s=sum(n); s=s*s%modd;
for (ll i=2,nxt;i<=n;i=nxt+1) {
nxt=n/(n/i);
s-=(sq(nxt)-sq(i-1))*calc(n/i)%modd; s%=modd;
}
Phi[n]=(s+modd)%modd;
return (s+modd)%modd;
}
int main() {
scanf("%lld%lld",&modd,&n);
Inv2=quick(2,modd-2); Inv6=quick(6,modd-2);
init();
for (ll i=1,nxt=1;i<=n;i=nxt+1) {
nxt=n/(n/i);
ll ss=sum(n/i); ss=ss*ss%modd;
ans+=ss*(calc(nxt)-calc(i-1))%modd;
ans=(ans+modd)%modd;
}
printf("%lld
",(ans+modd)%modd);
return 0;
}
（三）(bzoj2693)，(P4313)
求
[sum_{i=1}^{n}sum_{i=1}^{m}lcm(i,j)
]
ymy大佬的博客中推导过程和我一样的，所以我就懒得写了
[=sumlimits_{i=1}^nsumlimits_{j=1}^m frac{ij}{gcd(i,j)}
]
[=sumlimits_{d=1}^n frac{1}{d}sumlimits_{i=1}^{n}sumlimits_{j=1}^{m} ij[gcd(i,j)=d]
=sumlimits_{d=1}^n dsumlimits_{i=1}^{lfloorfrac{n}{d}
floor}sumlimits_{j=1}^{lfloorfrac{m}{d}
floor} ij[gcd(i,j)=1]]
[=sumlimits_{d=1}^n dsumlimits_{i=1}^{lfloorfrac{n}{d}
floor}sumlimits_{j=1}^{lfloorfrac{m}{d}
floor} ijsumlimits_{x|gcd(i,j)}mu(x)
=sumlimits_{d=1}^n dsumlimits_{x=1}^{lfloorfrac{n}{d}
floor}mu(x)x^2sumlimits_{i=1}^{lfloorfrac{n}{dx}
floor}sumlimits_{j=1}^{lfloorfrac{m}{dx}
floor} ij]
设(f(T)=sumlimits_{i=1}^{lfloorfrac{n}{T} floor}sumlimits_{j=1}^{lfloorfrac{m}{T} floor} ij=sumlimits_{i=1}^{lfloorfrac{n}{T} floor}isumlimits_{j=1}^{lfloorfrac{m}{T} floor}j)，所以
[=sumlimits_{T=1}^n f(T)sumlimits_{d|T}mu(d)*d^2frac{T}{d}
=sumlimits_{T=1}^n f(T)*Tsumlimits_{d|T}mu(d)*d]
设(g(n)=sumlimits_{d|n}mu(d)*d) ,则(g) 为积性函数，可以线筛。
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
typedef long long ll;
typedef double dd;
#define For(i,j,k) for (int i=j;i<=k;++i)
#define Forr(i,j,k) for (int i=j;i>=k;--i)
#define Set(a,p) memset(a,p,sizeof(a))
using namespace std;
template<typename T>bool chkmax(T& a,T b) {return a<b?a=b,1:0;}
template<typename T>bool chkmin(T& a,T b) {return a>b?a=b,1:0;}
const int maxn=10000000+100;
const int maxx=10000000;
const ll modd=100000009;
int n,m,N;
int vis[maxn],p[maxn];
ll inv;
ll f[maxn],sum[maxn];
inline void read(int &x) {
x=0;
int p=1;
char c=getchar();
while (!isdigit(c)) {if (c=='-') p=-1; c=getchar();}
while (isdigit(c)) {x=(x<<1)+(x<<3)+(c-'0'); c=getchar();}
x*=p;
}
inline void init() {
f[1]=1;
For (i,2,maxx) {
if (!vis[i]) {
p[++N]=i; f[i]=1-i;
}
For (j,1,N) {
int k=i*p[j];
if (k>maxx) break;
vis[k]=1;
if (i%p[j]==0) {
f[k]=f[i]; break;
}
else f[k]=f[i]*(1-p[j])%modd;
}
}
For (i,1,maxx) f[i]=(f[i-1]+f[i]*i%modd+modd)%modd;
For (i,1,maxx) {
sum[i]=sum[i-1]+i;
if (sum[i]>modd) sum[i]-=modd;
}
}
int main() {
init();
int tt; read(tt);
while (tt--) {
ll ans=0;
read(n); read(m);
if (n>m) swap(n,m);
for (int i=1,nxt;i<=n;i=nxt+1) {
nxt=min(n/(n/i),m/(m/i));
ans+=sum[n/i]*sum[m/i]%modd*(f[nxt]-f[i-1])%modd;
ans%=modd;
}
printf("%lld
",(ans+modd)%modd);
}
return 0;
}
（四）(bzoj3994)
设 (d(n)) 为 (n) 的约数个数，求
[sum_{i=1}^{n}sum_{j=1}^{m}d(ij)
]
分析：
[=sum_{i=1}^{n}sum_{j=1}^{m}sum_{p|i}sum_{q|j}[gcd(p,q)=1]
]
[=sum_{p=1}^{n}sum_{q=1}^{m}leftlfloor frac{n}{p}
ight
floor leftlfloor frac{m}{q}
ight
floor[gcd(p,q)=1]
]
[=sum_{i=1}^{n}sum_{j=1}^{m}leftlfloor frac{n}{i}
ight
floor leftlfloor frac{m}{j}
ight
floor[gcd(i,j)=1]
]
[=sum_{d=1}^{n}mu(d)sum_{i=1}^{leftlfloor frac{n}{d}
ight
floor}sum_{j=1}^{leftlfloor frac{m}{d}
ight
floor}leftlfloor frac{n}{id}
ight
floorleftlfloor frac{m}{id}
ight
floor
]
然后，一个智障的变化，我一下子还没想出来
[=sum_{d=1}^{n}mu(d)sum_{i=1}^{leftlfloor frac{n}{d}
ight
floor}leftlfloor frac{n}{id}
ight
floorsum_{j=1}^{leftlfloor frac{m}{d}
ight
floor}leftlfloor frac{m}{id}
ight
floor
]
设
[f(n)=sum_{i=1}^{n}leftlfloor frac{n}{i}
ight
floor
]
这个显然可以分块，然后就可以化为
[=sum_{d=1}^{n}mu(d)f(leftlfloor frac{n}{d}
ight
floor)f(leftlfloor frac{m}{d}
ight
floor)
]
后面的在 (O(nsqrt{n})) 预处理之后可以 (O(1)) 计算，前面的分块 (O(sqrt{n}))
总时间复杂度 (O(nsqrt{n}+Tsqrt{n}))
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
typedef long long ll;
typedef double dd;
#define For(i,j,k) for (register int i=j;i<=k;++i)
#define Forr(i,j,k) for (register int i=j;i>=k;--i)
#define Set(a,p) memset(a,p,sizeof(a))
using namespace std;
template<typename T>bool chkmax(T &a,T b) { return a<b?a=b,1:0; }
template<typename T>bool chkmin(T &a,T b) { return a>b?a=b,1:0; }
const int maxn=50000+100;
const int maxx=50000;
int n,m,N;
int p[maxn],vis[maxn],mu[maxn],sum[maxn],s[maxn];
inline void read(int &x) {
x=0;
int p=1;
char c=getchar();
while (!isdigit(c)) {if (c=='-') p=-1; c=getchar();}
while (isdigit(c)) {x=(x<<1)+(x<<3)+(c-'0'); c=getchar();}
x*=p;
}
inline void init() {
mu[1]=1;
For (i,2,maxx) {
if (!vis[i]) {
p[++N]=i; mu[i]=-1;
}
For (j,1,N) {
if (i*p[j]>maxx) break;
int k=i*p[j];
vis[k]=1;
if (i%p[j]==0) {
mu[k]=0; break;
}
else mu[k]=-mu[i];
}
}
For (i,1,maxx) {
sum[i]=sum[i-1]+mu[i];
for (int p=1,nxt=1;p<=i;p=nxt+1) {
nxt=i/(i/p);
s[i]+=(nxt-p+1)*(i/p);
}
}
}
inline void solve() {
if (n>m) swap(n,m);
ll ans=0;
for (int i=1,nxt=1;i<=n;i=nxt+1) {
nxt=min(n/(n/i),m/(m/i));
ans+=1ll*s[n/i]*s[m/i]*(sum[nxt]-sum[i-1]);
}
printf("%lld
",ans);
}
int main() {
init();
int tt; read(tt);
while (tt--) {
read(n); read(m);
solve();
}
return 0;
}